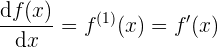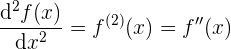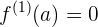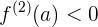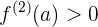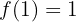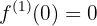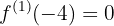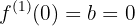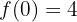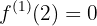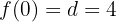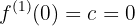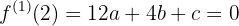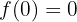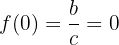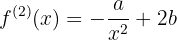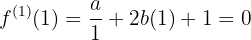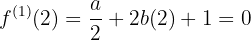Kapitel
Zunächst einmal führst Du eine alternative Schreibweise für die Ableitungen einer Funktion  .
.
Der Grund für die Einführung alternativer Schreibweisen für ein und dasselbe Konzept liegt darin, dass es Fälle gibt, in denen die Entwicklungen sehr umfangreich oder kompliziert sind und es notwendig ist, die Funktion weniger umfangreich zu gestalten, um sie praktikabler zu machen, da es hier darauf ankommt, dass sie weiterhin dasselbe Konzept darstellen.
Die erste Ableitung einer Funktion hat drei Bezeichnungen, die du hier vorfindest:
und die zweite Ableitung einer Funktion (die Ableitung der Ableitung), hat die folgenden alternativen Schreibweisen:
in diesem Fall verwendest Du der Übersichtlichkeit halber die Schreibweise 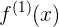 für die erste Ableitung und
für die erste Ableitung und 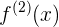 für die zweite Ableitung.
für die zweite Ableitung.
Nachdem Du die Schreibweise festgelegt hast, die Du verwenden wirst, untersuchst Du nun einige Eigenschaften der Funktionen.
Genauer gesagt, solltest Du die Kriterien kennen, die Dir sagen, wo eine Funktion ihren höchst- oder niedrigstmöglichen Wert innerhalb einer bestimmten Region erreicht, weshalb sie als relatives Maximum oder Minimum bezeichnet werden.

Relative Extremwerte
Einfach ausgedrückt handelt es sich dabei um Punkte, an denen eine Funktion einen maximalen oder minimalen Wert erreicht, und zwar im Vergleich zu den Punkten einer Umgebung, die sich in ihrer Nähe befinden. Diese Art von Punkten wird als relative Extrempunkte bezeichnet.
Wenn 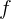 eine ableitbare Funktion in
eine ableitbare Funktion in 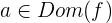 , ist, dann ist
, ist, dann ist  ein relatives oder lokales Extremum, wenn:
ein relatives oder lokales Extremum, wenn:
Relatives Maximum
Wenn 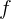 eine ableitbare Funktion in
eine ableitbare Funktion in 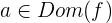 ist, dann ist
ist, dann ist  ein relatives oder lokales Maximum, wenn:
ein relatives oder lokales Maximum, wenn:
Relative Minima
Wenn 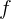 eine ableitbare Funktion in
eine ableitbare Funktion in 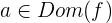 ist, dann ist
ist, dann ist  ein relatives oder lokales Minimum, wenn:
ein relatives oder lokales Minimum, wenn:
Berechnung von Maxima und Minima
Betrachte die folgende Funktion 
Um die lokalen Extremitäten zu finden, gehst Du wie folgt vor:
1 Finde die erste Ableitung der Funktion und berechne ihre Wurzeln.
Zunächst die Ableitung der Funktion

Nun ihre Wurzeln, die Lösung der Gleichung

Ihre Wurzeln sind also

2Nimm die zweite Ableitung und berechne das Vorzeichen der Wurzeln.
Berechne die zweite Ableitung der Funktion.

Bewerte die in der zweiten Ableitung erhaltenen Wurzeln
 ,
,  bei
bei  hat die Funktion ein relatives Maximum
hat die Funktion ein relatives Maximum
 ,
,  bei
bei  hat die Funktion ein relatives Minimum
hat die Funktion ein relatives Minimum
3Berechne die Bildmenge (in der Funktion) der relativen Extrema.
 ,
, bei
bei  hat der Graph der Funktion ein relatives Maximum
hat der Graph der Funktion ein relatives Maximum
 ,
,  bei
bei  hat der Graph der Funktion ein relatives Minimum
hat der Graph der Funktion ein relatives Minimum
Untersuchung der relativen Extremwerte des Wachstums
Da Du Dich bereits mit dem Wachstum und der Abnahme einer Funktion beschäftigt hast, wird es sie folgendermaßen geben:
- Ein Maximum am Punkt der Funktion, wenn die Funktion von steigendem
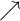 zu fallendem
zu fallendem  übergeht.
übergeht. - Ein Minimum an dem Punkt der Funktion, an dem die Funktion von fallendem
 zu steigendem
zu steigendem  übergeht.
übergeht.
Beispiel:
Betrachte die folgende Funktion 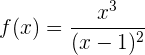
Um die lokalen Extremitäten zu finden, gehst Du wie folgt vor:
1 Bestimme den Definitionsbereich der Funktion, die erste Ableitung und berechne ihre Wurzeln.
Zunächst der Definitionsbereich der Funktion
Suche die Punkte, an denen die Funktion unbestimmt ist, d. h. Werte, bei denen 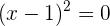
.
Dieser Wert ist  , er ist der Wert, den Du entfernen musst, also
, er ist der Wert, den Du entfernen musst, also 
.
Berechne nun die Ableitung der Funktion

Nun ihre Wurzeln, die Lösung der Gleichung
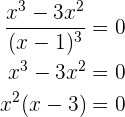
Ihre Wurzeln sind

2Nimm die berechneten Werte und erzeuge Sektoren der realen Linie.
Nimm dann einen Wert aus jedem Sektor, werte ihn in der ersten Ableitung aus und beobachte die erhaltenen Vorzeichen, um die Art der Funktion in jedem Sektor zu analysieren.
Nimm die berechneten Werte und erzeuge Sektoren aus der realen Linie
Die Werte sind 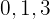 , dann sind die Sektoren
, dann sind die Sektoren 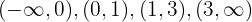
Bewerte ein Element jedes Sektors in der ersten Ableitung
- Sei
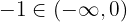 , entonces
, entonces 
 in
in  ist die Funktion steigend
ist die Funktion steigend 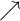
- Sei
 , dann ist
, dann ist 
 in
in 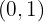 ist die Funktion steigend
ist die Funktion steigend 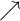
- Sei
 , dann ist
, dann ist 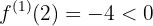
 in
in 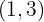 ist die Funktion abnehmend
ist die Funktion abnehmend 
- Sei
 , dann ist
, dann ist 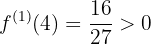
 in
in 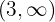 ist die Funktion steigend
ist die Funktion steigend 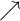
In der folgenden Tabelle sind die erhaltenen Informationen aufgeführt:
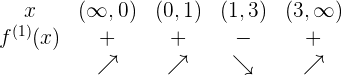
3Interpretiere die Informationen und ermittle das Maximum oder Minimum.
Du stellst fest, dass zwei Vorzeichenwechsel erzeugt werden, wobei der von 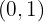 nach
nach 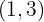 verworfen wird, da hier die Unbestimmtheit vorliegt.
verworfen wird, da hier die Unbestimmtheit vorliegt.
Der nächste Vorzeichenwechsel ist von 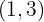 zu
zu 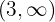 , und da er von abnehmend zu ansteigend ist, hat man bei
, und da er von abnehmend zu ansteigend ist, hat man bei 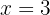 ein relatives Minimum
ein relatives Minimum
4 Bewerte die Zahl in der Funktion, um den Punkt in der Ebene zu bestimmen.
Du siehst, dass 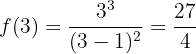 , also am Punkt
, also am Punkt  , die Funktion ein relatives Minimum hat.
, die Funktion ein relatives Minimum hat.
Übungsaufgaben
Betrachte die folgende Funktion 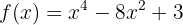
1 Finde die erste Ableitung der Funktion und berechne ihre Wurzeln.
Zunächst die Ableitung der Funktion
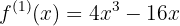
Nun ihre Wurzeln, die Lösung der Gleichung

Ihre Wurzeln sind

2 Nimm die zweite Ableitung und berechne das Vorzeichen der Wurzeln.
Berechne die zweite Ableitung der Funktion
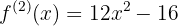
Bewerte die in der zweiten Ableitung erhaltenen Wurzeln
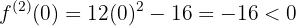 ,
,  bei
bei  hat die Funktion ein relatives Maximum
hat die Funktion ein relatives Maximum
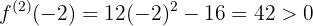 ,
,  bei
bei  hat die Funktion ein relatives Minimum
hat die Funktion ein relatives Minimum
 ,
,  bei
bei  hat die Funktion ein relatives Minimum
hat die Funktion ein relatives Minimum
3 Berechne die Bildmenge (in der Funktion) der relativen Extrema.
 ,
,  bei
bei  hat der Graph der Funktion ein relatives Minimum
hat der Graph der Funktion ein relatives Minimum
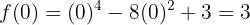 ,
, bei
bei 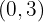 hat der Graph der Funktion ein relatives Maximum
hat der Graph der Funktion ein relatives Maximum
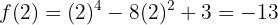 ,
,  bei
bei  hat der Graph der Funktion ein relatives Minimum
hat der Graph der Funktion ein relatives Minimum
Betrachte die folgende Funktion 
1 Finde die erste Ableitung der Funktion und berechne ihre Wurzeln.
Zunächst die Ableitung der Funktion
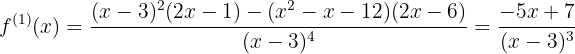
Nun ihre Wurzeln, die Lösung der Gleichung
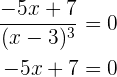
bedeutet, dass ihre Wurzel
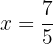
2 Nimm die zweite Ableitung und berechne das Vorzeichen der Wurzeln.
Berechne die zweite Ableitung der Funktion

Berechne die Wurzel aus der zweiten Ableitung
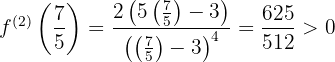 ,
,  bei
bei 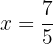 hat die Funktion ein relatives Minimum
hat die Funktion ein relatives Minimum
3 Berechne die Bildmenge (in der Funktion) der relativen Extrema.
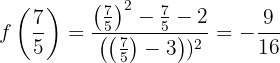
 bei
bei 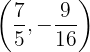 hat der Graph der Funktion ein relatives Minimum
hat der Graph der Funktion ein relatives Minimum
Betrachte die folgende Funktion 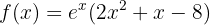
1 Finde die erste Ableitung der Funktion und berechne ihre Wurzeln.
Zunächst die Ableitung der Funktion

Nun ihre Wurzeln, die Lösung der Gleichung

bedeutet, dass ihre Wurzeln
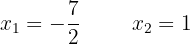
2Nimm die zweite Ableitung und berechne das Vorzeichen der Wurzeln.
Berechne die zweite Ableitung der Funktion
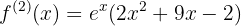
Bewerte die in der zweiten Ableitung erhaltenen Wurzeln
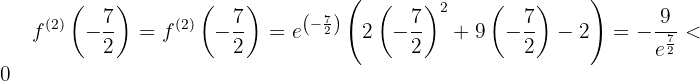 ,
,  bei
bei 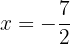 , hat die Funktion ein relatives Maximum
, hat die Funktion ein relatives Maximum
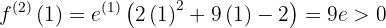 ,
,  e bei
e bei  hat die Funktion ein relatives Minimum
hat die Funktion ein relatives Minimum
3 Berechne die Bildmenge (in der Funktion) der relativen Extrema.
 ,
,  bei
bei 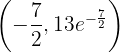 hat der Graph der Funktion ein relatives Maximum
hat der Graph der Funktion ein relatives Maximum
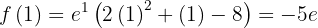 ,
,  bei
bei 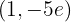 hat der Graph der Funktion ein relatives Minimum
hat der Graph der Funktion ein relatives Minimum
Betrachte die folgende Funktion 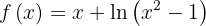 .
.
In diesem Fall ist es notwendig, den Definitionsbereich zu berücksichtigen, da Du möglicherweise Werte verwerfen musst, die nicht zu ihr gehören.
Das sollte eigentlich immer gemacht werden, aber es wird nicht gemacht, wenn klar ist, was der Definitionsbereich ist.
0 Finde den Definitionsbereich der Funktion
Der Definitionsbereich der natürlichen Logarithmusfunktion ist derjenige, in dem das Argument positiv ist, also musst Du 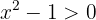 lösen
lösen
Die Lösungen von 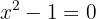 son
son 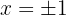 . Das bedeutet, dass Du die Sektoren
. Das bedeutet, dass Du die Sektoren 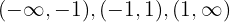 erzeugen musst, und von dort eine Zahl aus jedem Sektor nimmst, sie in
erzeugen musst, und von dort eine Zahl aus jedem Sektor nimmst, sie in 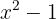 auswertest und das erzeugte Vorzeichen kennst, um schließlich zu lösen.
auswertest und das erzeugte Vorzeichen kennst, um schließlich zu lösen.

Das bedeutet, dass die Lösung der Ungleichung, also der Bereich der Funktion, 
1Finde die erste Ableitung der Funktion und berechne ihre Wurzeln.
Zunächst die Ableitung der Funktion
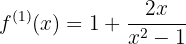
Nun ihre Wurzeln, die Lösung der Gleichung
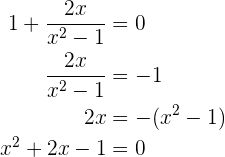
Ihre Wurzeln sind

Ignoriere 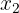 , da
, da 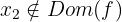
2 Nimm die zweite Ableitung und berechne das Vorzeichen der Wurzeln.
Berechne die zweite Ableitung der Funktion
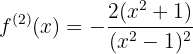
Bewerte die in der zweiten Ableitung erhaltenen Wurzeln
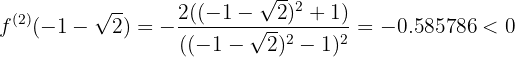 ,
,  bei
bei 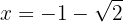 Funktion hat relatives Maximum
Funktion hat relatives Maximum
3 Berechne die Bildmenge (in der Funktion) der relativen Extrema.
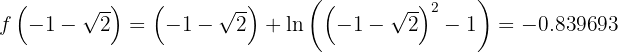 ,
, bei
bei  hat der Graph der Funktion ein relatives Maximum
hat der Graph der Funktion ein relatives Maximum
Betrachte die folgende Funktion 
1 Finde die erste Ableitung der Funktion und berechne ihre Wurzeln.
Zunächst die Ableitung der Funktion
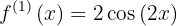
Nun ihre Wurzeln, die Lösung der Gleichung
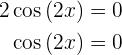
Ihre Wurzeln sind
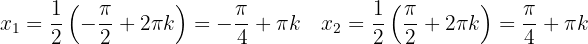 , con
, con 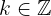
2 Nimm die zweite Ableitung und berechne das Vorzeichen der Wurzeln.
Berechne die zweite Ableitung der Funktion

Bewerte die in der zweiten Ableitung erhaltenen Wurzeln
 ,
,  bei
bei  hat die Funktion ein relatives Minimum für jedes
hat die Funktion ein relatives Minimum für jedes 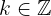
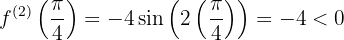 ,
,  bei
bei 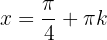 hat die Funktion ein relatives Maximum für jedes
hat die Funktion ein relatives Maximum für jedes 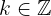
3 Berechne die Bildmenge (in der Funktion) der relativen Extrema.
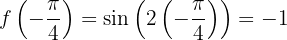 ,
,  bei
bei 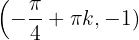 hat der Graph der Funktion ein relatives Minimum für jedes
hat der Graph der Funktion ein relatives Minimum für jedes 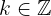
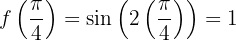 ,
,  bei
bei 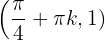 hat der Graph der Funktion ein relatives Maximum für jedes para cada
hat der Graph der Funktion ein relatives Maximum für jedes para cada 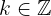
Probleme
Bestimme  ,
, y
y  so, dass die Funktion
so, dass die Funktion 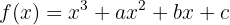 ein Maximum für
ein Maximum für 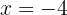 , hat, ein Minimum für
, hat, ein Minimum für  , und den Wert
, und den Wert 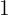 para
para  annimmt.
annimmt.
Das Problem äußert sich darin, dass die folgenden Bedingungen eintreten:
was bedeutet, dass Du die erste Ableitung der Funktion berechnen musst

und mit diesem die Bewertungen durchführen
Erstelle ein Drei-mal-Drei-Gleichungssystem
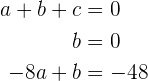
dessen Lösung 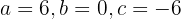 ist
ist
Bestimme den Wert von  ,
, ,
, und
und 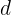 so dass die Funktion
so dass die Funktion 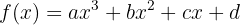 ein Maximum bei
ein Maximum bei  und ein Minimum bei
und ein Minimum bei 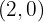 hat.
hat.
Das Problem äußert sich darin, dass die folgenden Bedingungen eintreten:
bedeutet, dass Du die erste Ableitung der Funktion berechnen musst

und nimm dann die entsprechenden Bewertungen vor
die das folgende Vier-mal-Vier-Gleichungssystem erzeugen
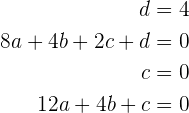
dessen Lösung 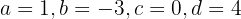 ist
ist
Gegeben ist die Funktion: 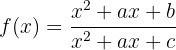
Berechne  ,
, und
und  , so dass
, so dass  bei
bei 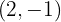 ein lokales Extremum hat und die Kurve durch den Koordinatenursprung verläuft.
ein lokales Extremum hat und die Kurve durch den Koordinatenursprung verläuft.
Das Problem äußert sich darin, dass die folgenden Bedingungen eintreten:
bedeutet, dass Du die erste Ableitung der Funktion berechnen musst
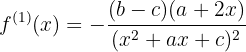
und nimm dann die entsprechenden Bewertungen vor
das folgende Drei-mal-Drei-Gleichungssystem erzeugt
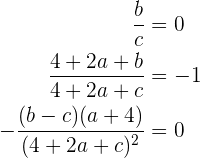
dessen Lösung 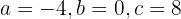 ist
ist
Fince  y
y  so, dass die Funktion:
so, dass die Funktion: 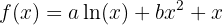 Extrema an den Punkten
Extrema an den Punkten 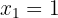 y
y 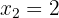 hat. Für diese Werte von
hat. Für diese Werte von  und
und  , welche Art von Extremen hat die Funktion in
, welche Art von Extremen hat die Funktion in 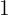 und in
und in 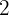 ?
?
Berechne die erste und die zweite Ableitung der Funktion, um die Bedingungen zu finden, unter denen sie extrem sind, und um ihre Art zu kennen.
Da Du nun willst, dass die Funktion an den Punkten 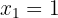 und
und 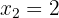 ,
,
Extrema hat, stellst Du folgende Gleichungen auf
ein System wird erzeugt, dessen Lösung ist:  und
und 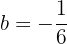 .
.
Du hast bereits die Werte gefunden, die dazu führen, dass die Funktion an der angegebenen Stelle Extremwerte aufweist, nun willst Du ihre Art ansehen. Hierfür benötigst Du die zweite Ableitung der Funktion:

Schaue dir nun die Art der einzelnen Enden an
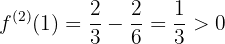 ,
,  bei
bei 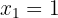 , hat die Funktion ein relatives Minimum
, hat die Funktion ein relatives Minimum ,
,  bei
bei 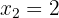 , hat die Funktion ein relatives Maximum
, hat die Funktion ein relatives Maximum
Mit KI zusammenfassen: