Kapitel
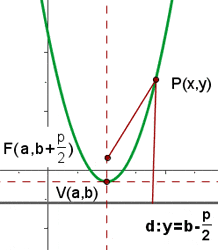
Im kartesischen Koordinatensystem wird als Parabel der Raum bezeichnet, der durch die Punkte 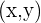 , die von einem festen Punkt, dem sogenannten Brennpunkt und einer gegebenen Geraden, der sogenannten Leitlinie gleich weit entfernt sind. Bei einer Parabel mit gegebenen Brennpunkt
, die von einem festen Punkt, dem sogenannten Brennpunkt und einer gegebenen Geraden, der sogenannten Leitlinie gleich weit entfernt sind. Bei einer Parabel mit gegebenen Brennpunkt  und einer Leitlinie
und einer Leitlinie  liegen die Punkte
liegen die Punkte  dann auf der Parabel, wenn sie folgendes erfüllen:
dann auf der Parabel, wenn sie folgendes erfüllen:
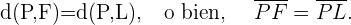
Der Abstand zwischen  und
und  wird als Brennweite
wird als Brennweite  bezeichnet; diese erhält man, indem man eine Senkrechte
bezeichnet; diese erhält man, indem man eine Senkrechte  darstellt, die durch
darstellt, die durch  verläuft. Anschließend berechnet man den Abstand auf der Senkrechten zwischen Leitlinie und Brennpunkt. Der höchste (bzw. tiefste oder äußerste) Punkt der Parabel wird als Scheitelpunkt
verläuft. Anschließend berechnet man den Abstand auf der Senkrechten zwischen Leitlinie und Brennpunkt. Der höchste (bzw. tiefste oder äußerste) Punkt der Parabel wird als Scheitelpunkt 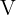 bezeichnet. Sein Abstand ist sowohl zum Brennpunkt als auch zur Leitlinie
bezeichnet. Sein Abstand ist sowohl zum Brennpunkt als auch zur Leitlinie  . Aus geometrischer Perspektive bildet er den Mittelpunkt der Geraden zwischen Brennpunkt und Leitlinie, das heißt, auf der Mitte der Linie, die die Brennweite darstellt.
. Aus geometrischer Perspektive bildet er den Mittelpunkt der Geraden zwischen Brennpunkt und Leitlinie, das heißt, auf der Mitte der Linie, die die Brennweite darstellt.

Gleichung einer Normalparabel mit horizontaler Hauptachse
Wir nehmen an, dass die Leitlinie unserer Parabel eine vertikale Gerade ist, die links von der x-Achse parallel zur Koordinatenachse verläuft. Wenn die Koordinaten des Scheitelpunkts 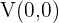 sind, müssen die Koordinaten des Brennpunkts folglich
sind, müssen die Koordinaten des Brennpunkts folglich 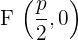 sein und die Leitlinie
sein und die Leitlinie 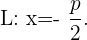
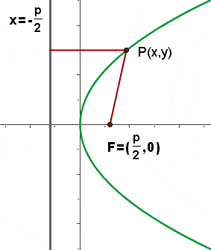
Die Punkte  befinden sich auf der Parabel, wenn ihr Abstand zum Brennpunkt derselbe wie zur Leitlinie ist, das heißt:
befinden sich auf der Parabel, wenn ihr Abstand zum Brennpunkt derselbe wie zur Leitlinie ist, das heißt:
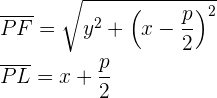

Durch Vereinfachen des Ausdrucks erhält man die Gleichung für eine Normalparabel mit rechtsseitiger Öffnung:
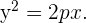
Für den umgekehrten Fall mit einer Geraden rechts der x-Achse und den Koordinaten des Scheitelpunkts 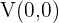 , wären die Koordinaten des Brennpunkts
, wären die Koordinaten des Brennpunkts 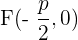 und die Leitlinie
und die Leitlinie 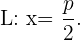
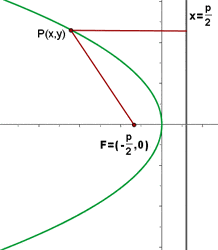
Folgt man dem vorherigen Rechenverfahren, erhält man die Gleichung für eine Normalparabel mit linksseitiger Öffnung:
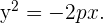
Beispiele
1 Gegeben sei die Parabel 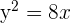 . Berechne ihren Scheitelpunkt, Brennpunkt sowie ihre Leitlinie.
. Berechne ihren Scheitelpunkt, Brennpunkt sowie ihre Leitlinie.


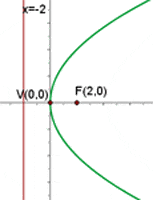
2 Gegeben sei die Parabel 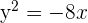 . Berechne ihren Scheitelpunkt, Brennpunkt sowie ihre Leitlinie.
. Berechne ihren Scheitelpunkt, Brennpunkt sowie ihre Leitlinie.

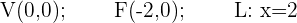
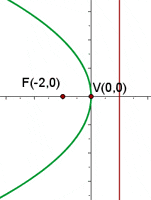
Gleichung einer Normalparabel mit vertikaler Hauptachse
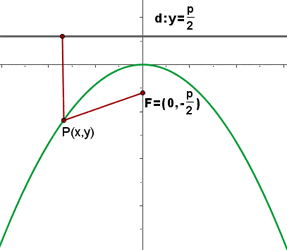
Wir nehmen an, dass die Leitlinie unserer Parabel eine horizontale Gerade ist, die parallel zur Abszissenachse verläuft, welche unterhalb dieser liegt. Wenn die Koordinaten des Scheitelpunkts 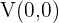 sind, müssen die Koordinaten des Brennpunkts folglich
sind, müssen die Koordinaten des Brennpunkts folglich 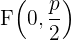 sein und die Leitlinie
sein und die Leitlinie 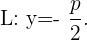
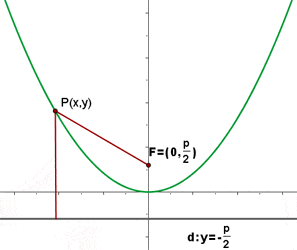
Die Punkte  befinden sich auf der Parabel, wenn ihr Abstand zum Brennpunkt derselbe wie zur Leitlinie ist, das heißt:
befinden sich auf der Parabel, wenn ihr Abstand zum Brennpunkt derselbe wie zur Leitlinie ist, das heißt:
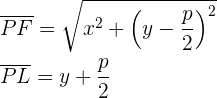
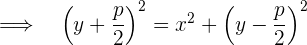
Durch Vereinfachen des Ausdrucks erhält man die Gleichung für eine Normalparabel mit rechtsseitiger Öffnung:

Für den umgekehrten Fall, dass die Gerade oberhalb der Abszissenachse verläuft und der Scheitelpunkt die Koordinaten 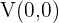 besitzt, läge der Brennpunkt bei
besitzt, läge der Brennpunkt bei 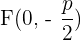 und die Leitlinie wäre
und die Leitlinie wäre 
Folgt man dem vorherigen Rechenverfahren, erhält man die Gleichung für eine Normalparabel mit linksseitiger Öffnung:
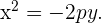
Beispiele
1 Gegeben sei die Parabel 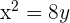 . Berechne ihren Scheitelpunkt, Brennpunkt sowie ihre Leitlinie.
. Berechne ihren Scheitelpunkt, Brennpunkt sowie ihre Leitlinie.


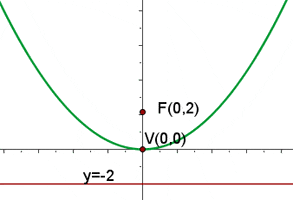
2 Gegeben sei die Parabel 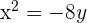 . Berechne ihren Scheitelpunkt, Brennpunkt sowie ihre Leitlinie.
. Berechne ihren Scheitelpunkt, Brennpunkt sowie ihre Leitlinie.

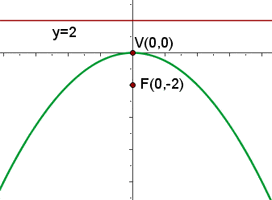
Gewöhnliche Parabelgleichungen
Bei Parabeln mit einem Scheitelpunkt der Koordinaten  ungleich Null sind die zugehörigen Gleichungen sehr ähnlich zu denen der Normalparabel, jedoch ist diese im Koordinatensystem verschoben.
ungleich Null sind die zugehörigen Gleichungen sehr ähnlich zu denen der Normalparabel, jedoch ist diese im Koordinatensystem verschoben.
Die Leitlinie verläuft parallel zur Koordinatenachse.
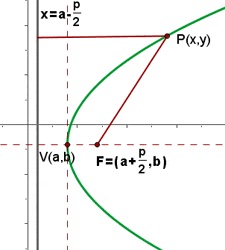

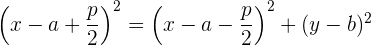
Durch Vereinfachen des Ausdrucks erhält man die Gleichung für eine gewöhnliche Parabel mit rechtsseitiger Öffnung:

Ist der Wert von  negativ, bedeutet das, dass die Parabel nach links geöffnet ist.
negativ, bedeutet das, dass die Parabel nach links geöffnet ist.
Die Leitlinie verläuft parallel zur Abszissenachse.
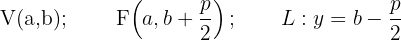
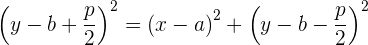
Durch Vereinfachen des Ausdrucks erhält man die Gleichung für eine gewöhnliche Parabel mit Öffnung nach oben:

Ist der Wert von  negativ, bedeutet das, dass die Parabel nach unten geöffnet ist.
negativ, bedeutet das, dass die Parabel nach unten geöffnet ist.
Beispiele
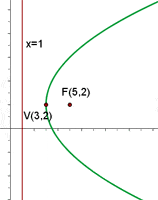
2 Gegeben sei die Parabel 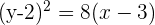 . Berechne ihren Scheitelpunkt, Brennpunkt sowie ihre Leitlinie.
. Berechne ihren Scheitelpunkt, Brennpunkt sowie ihre Leitlinie.

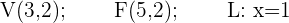
2 Gegeben sei die Parabel 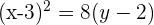 . Berechne ihren Scheitelpunkt, Brennpunkt sowie ihre Leitlinie.
. Berechne ihren Scheitelpunkt, Brennpunkt sowie ihre Leitlinie.

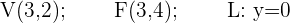
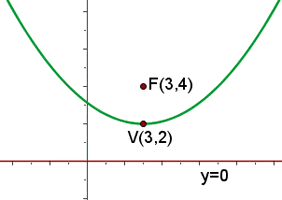
Gemischte Aufgaben zu Parabelgleichungen
Bestimme die Parabelgleichungen anhand der vorgegebenen Informationen:
Leitlinie  , Brennpunkt
, Brennpunkt 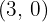 .
.
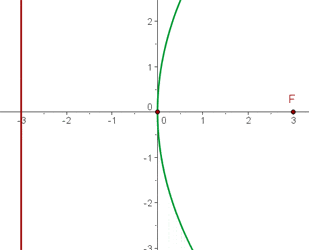
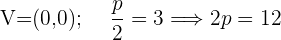
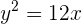
Leitlinie  , Scheitelpunkt
, Scheitelpunkt  .
.
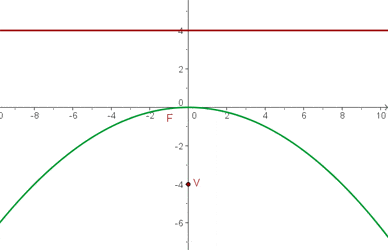
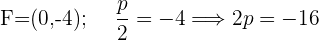
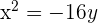
Leitlinie 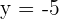 , Brennpunkt
, Brennpunkt  .
.

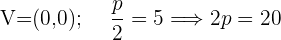
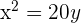
Leitlinie  , Brennpunkt
, Brennpunkt 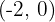 .
.
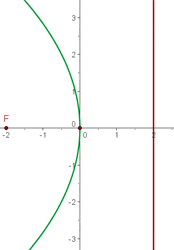
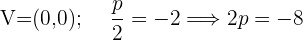
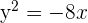
Brennpunkt  , Scheitelpunkt
, Scheitelpunkt  .
.
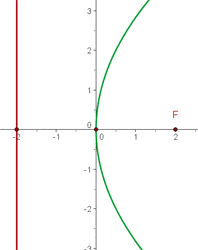
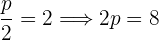
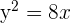
Brennpunkt 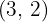 , Scheitelpunkt
, Scheitelpunkt 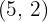 .
.
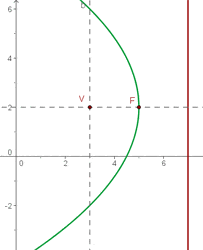

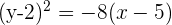
Brennpunkt 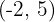 , Scheitelpunkt
, Scheitelpunkt  .
.
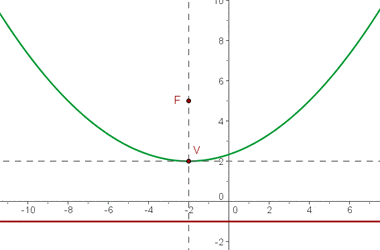
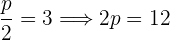

Brennpunkt  , Scheitelpunkt
, Scheitelpunkt 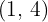 .
.
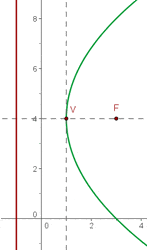
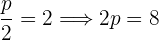

Berechne anhand der vorgegebenen Parabelgleichungen die Koordinaten ihres Scheitelpunkts, ihres Brennpunkts sowie die Gleichungen der Leitlinien.

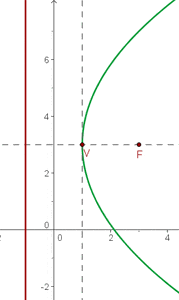
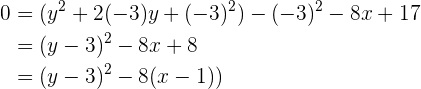
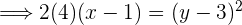
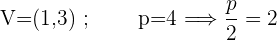

Berechne anhand der vorgegebenen Parabelgleichungen die Koordinaten ihres Scheitelpunkts, ihres Brennpunkts sowie die Gleichungen der Leitlinien.

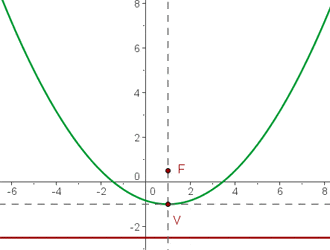
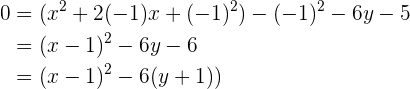
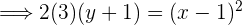
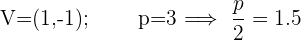

Berechne anhand der vorgegebenen Parabelgleichungen die Koordinaten ihres Scheitelpunkts, ihres Brennpunkts sowie die Gleichungen der Leitlinien.

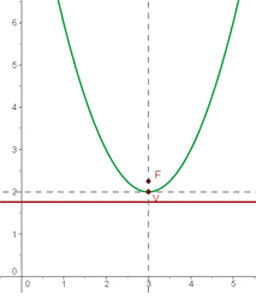
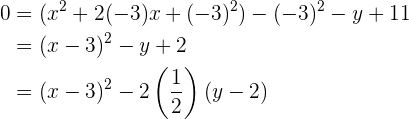


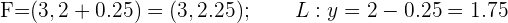
Bestimme die Gleichung der Parabel mit Leitlinie  und Brennpunkt
und Brennpunkt  .
.
Die Formel, die für die gewöhnliche Parabelgleichung verwendet wird, ist 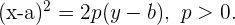
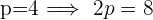

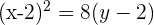
Bestimme die Gleichung einer Parabel mit vertikaler Hauptachse, deren Scheitelpunkt auf der Abszissenachse liegt und welche durch die Punkte 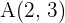 und
und 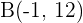 verläuft.
verläuft.
Die Formel, die für die gewöhnliche Parabelgleichung verwendet wird, ist 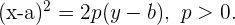 Der Scheitelpunkt entspricht der Form
Der Scheitelpunkt entspricht der Form  .Man bildet ein 2x2-Gleichungssystem mit zwei Unbekannten, in welche man die bekannten Punkte und den Wert des Scheitelpunkts einsetzt.
.Man bildet ein 2x2-Gleichungssystem mit zwei Unbekannten, in welche man die bekannten Punkte und den Wert des Scheitelpunkts einsetzt.
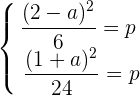
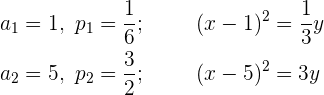
Mit KI zusammenfassen:













