Wir untersuchen den Unbestimmten Ausdruck der Form 0 geteilt durch 0 in zwei Fällen.
Fall 1: Rationale Funktion
Dies ist der Fall, wenn wir einen Bruch haben, bei dem Zähler und Nenner Polynome sind.
Das Verfahren zur Ermittlung des Grenzwerts bei einem unbestimmten Ausdruck der Form 0 geteilt durch 0 wird im Folgenden erläutert.
1 Bei dem Versuch, den Grenzwert zu berechnen, wird der unbestimmte Ausdruck der Form 0 geteilt durch 0 festgestellt.
2 Die Polynome des Zählers und des Nenners werden in Faktoren zerlegt
3 Der Bruch wird vereinfacht
4 Der Grenzwert des vereinfachten Ausdrucks wird berechnet
Beispiele
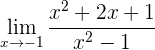
1 Wenn wir versuchen, den Grenzwert zu ermitteln, werden wir feststellen, dass er die Form 0/0 hat
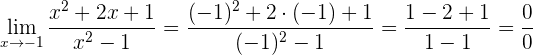
2 Wir faktorisieren
Der Zähler ist ein quadratisches Trinom, das als Binom zum Quadrat geschrieben werden kann.
Der Nenner ist eine Differenz von Quadraten, die gleich dem Produkt konjugierter Binome ist. Dies ist
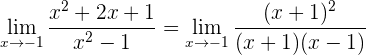
3 Wir vereinfachen den Bruch
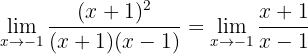
4 Nun berechnen wir den Grenzwert
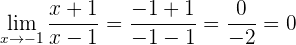
Der Grenzwert ist 0
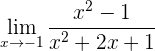
1 Wenn wir versuchen, den Grenzwert zu ermitteln, werden wir feststellen, dass er die Form 0/0 hat
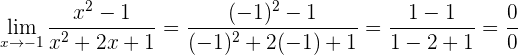
2 Wir faktorisieren
Der Zähler ist eine Differenz von Quadraten, die gleich dem Produkt konjugierter Binome ist.
Der Nenner ist ein quadratisches Trinom, das als Binom zum Quadrat geschrieben werden kann. Das heißt
3 Wir vereinfachen den Bruch
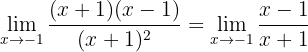
4 Nun berechnen wir den Grenzwert
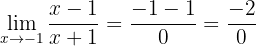
Da wir nur im Nenner die Null erhalten haben, müssen wir feststellen, ob dieser Grenzwert ins positive Unendliche oder ins negative Unendliche geht oder keinen Grenzwert hat (auf der einen Seite geht er ins positive Unendliche und auf der anderen ins negative Unendliche). Dazu nehmen wir die seitlichen Grenzwerte
Linksseitiger Grenzwert
Wenn wir 
einen Wert geben, der sich auf der linken Seite 
nähert, wie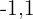 
; sind sowohl der Zähler als auch der Nenner negativ, so dass der linke Grenzwert negativ ist: 
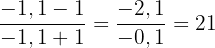
Rechtsseitiger Grenzwert
Wenn wir einen Wert geben, der sich auf der rechten Seite -1 nähert, wie -0,9. Der Zähler wird negativ und der Nenner positiv sein, so dass der Grenzwert auf der rechten Seite lautet: 
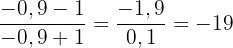
Da der linksseitige und der rechtsseitige Grenzwert nicht gleich sind, ergibt sich, dass es keinen Grenzwert bei x = -1 gibt.
Fall 2: Funktion mit Wurzeln
Dieser Fall trifft zu, wenn wir einen Bruch haben, der einen Rest hat, im Allgemeinen im Nenner.
Das Verfahren zur Ermittlung des Grenzwerts bei einem unbestimmten Ausdruck der Form 0 geteilt durch 0 wird im Folgenden erläutert.
1 Bei dem Versuch, den Grenzwert zu berechnen, wird der unbestimmte Ausdruch der Form 0 geteilt durch 0 festgestellt
2 Wir multiplizieren Zähler und Nenner mit dem Konjugierten des irrationalen Ausdrucks.
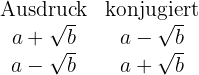
Beispiel:
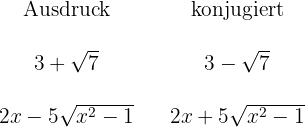
3 Wir führen die Rechenoperationen durch und vereinfachen den Bruch
Man beachte, dass ein irrationaler Ausdruck, multipliziert mit dem konjugierten Wert, eine Differenz von Quadraten ergibt
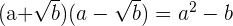
Beispiel:
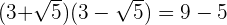
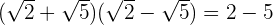
4 Wir berechnen den Grenzwert des vereinfachten Ausdrucks
Beispiel
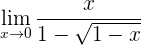
1 Bei dem Versuch, den Grenzwert zu berechnen, wird der unbestimmte Ausdruch der Form 0 geteilt durch 0 festgestellt
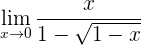
2 Wir multiplizieren und dividieren mit dem konjugierten Wert des Nenners
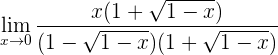
3 Wir führen die Rechenoperationen durch und vereinfachen den Bruch
Im Nenner haben wir Summe mal Differenz (konjugierte Binome), die gleich der Differenz der Quadrate ist
4 Wir berechnen den Grenzwert
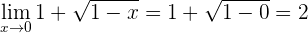
Der Grenzwert ist 2
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
