Bestimme das gleichschenklige Dreieck mit der größten Fläche, das in einen Kreis mit dem Radius 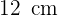 eingeschrieben ist.
eingeschrieben ist.
1 Wir stellen die Werte grafisch dar
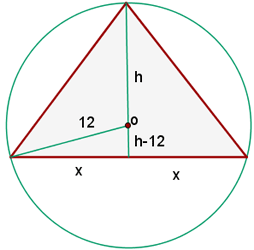
2 Die zu optimierende Funktion ist diejenige, die den Flächeninhalt des gleichschenkligen Dreiecks darstellt:
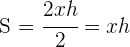
3 Wir setzen die Variablen in Beziehung:
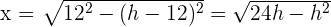
4 Wir setzen in die Funktion ein:

5 Wir leiten ab, setzen gleich 0 und berechnen die Nullstellen

Wir setzen gleich 0 (in diesem Fall nur den Zähler) und berechnen die Nullstellen

Wir setzen in Abhängigkeit von  und
und  . Wir erhalten
. Wir erhalten
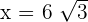
Die Grundseite ist 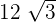
und die Seite ist
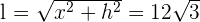
6 Wir führen die 2. Ableitung durch, um das erhaltene Ergebnis zu überprüfen.
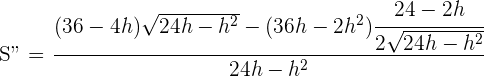
Für  erhalten wir
erhalten wir 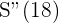 ein relatives Maximum gibt.
ein relatives Maximum gibt.
Ein gleichschenkliges Dreieck mit einem Umfang von 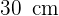 , dreht sich um seine Höhe und beschreibt einen Kegel.
, dreht sich um seine Höhe und beschreibt einen Kegel.
Welchen Wert muss die Grundfläche haben, damit das Volumen des Kegels maximal ist?
1 Wir stellen die Werte grafisch dar
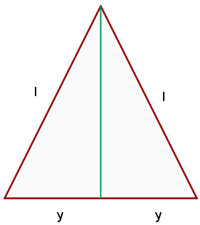
2 Die zu optimierende Funktion ist diejenige, die den Flächeninhalt des gleichschenkligen Dreiecks darstellt:

3 Wir setzen die Variablen in Beziehung:
Wir wenden den Satz des Pythagoras an
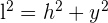
Wir wenden den Umfang an

Wir setzen die beiden Ausdrücke gleich und erhalten

4 Wir setzen in die Funktion:
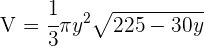
5 Wir leiten ab, setzen gleich 0 und berechnen die Nullstellen
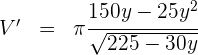
Wir setzen gleich 0 (in diesem Fall den Zähler) und berechnen die Nullstellen
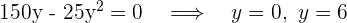
Die Grundseite ist 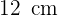
6 Wir führen die 2. Ableitung durch, um das erhaltene Ergebnis zu überprüfen
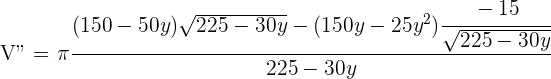
Für 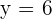 erhalten wir
erhalten wir 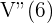 ein relatives Maximum gibt.
ein relatives Maximum gibt.
Ermittle die Maße des größten Rechtecks, das in ein gleichschenkliges Dreieck mit der Basis 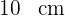 und der Höhe
und der Höhe 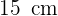 eingeschrieben ist.
eingeschrieben ist.
1 Wir stellen die Werte grafisch dar
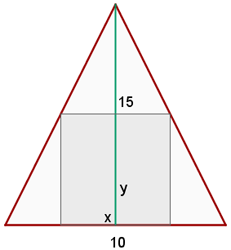
2 Zu optimierende Funktion

3 Wir setzen die Variablen in Beziehung: Da wir zwei ähnliche Dreiecke haben, erhalten wir

Wir wenden den Umfang an

4 Wir setzen in die Funktion ein:
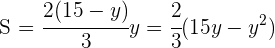
5 Wir leiten ab, setzen gleich 0 und berechnen die Nullstellen
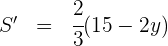
Wir setzen gleich 0 und berechnen die Nullstellen
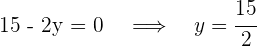
Die Grundseite ist 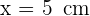
6 Wir führen die 2. Ableitung durch, um das erhaltene Ergebnis zu überprüfen.

Für  erhalten wir
erhalten wir 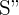 und
und  ein relatives Maximum.
ein relatives Maximum.
Ein Kreissegment hat einen Umfang von 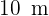 .
.
Berechne den Radius und die Breite des Segments mit der größten Fläche.
1 Wir stellen die Werte grafisch dar
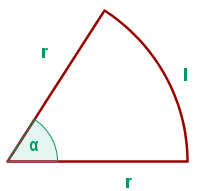
2 Zu optimierende Funktion
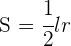
3 Wir setzen die Variablen in Beziehung:

4 Zu optimierende Funktion:
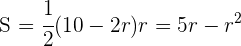
5 Wir leiten ab, setzen gleich 0 und berechnen die Nullstellen
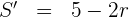
Wir setzen gleich 0 und berechnen die Nullstellen

Und schließlich 
6 Wir führen die 2. Ableitung durch, um das erhaltene Ergebnis zu überprüfen
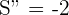
Für 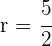 erhalten wir
erhalten wir 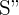 ,
, 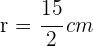 und
und  existiert also ein relatives Maximum.
existiert also ein relatives Maximum.
Ziel ist es, eine zylindrische Dose (mit Deckel) mit einem Fassungsvermögen von  Liter herzustellen.
Liter herzustellen.
Wie sollten die Maße sein, damit so wenig Metall wie möglich verwendet wird?
1 Zu optimierende Funktion

2 Wir setzen die Variablen in Beziehung:
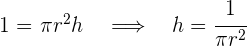
3 Wir setzen in die Funktion ein:

4 Wir leiten ab, setzen gleich 0 und berechnen die Nullstellen,

Wir setzen gleich 0 und berechnen die Nullstellen
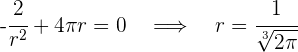
Somit 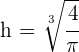
5 Wir führen die 2. Ableitung durch, um das erhaltene Ergebnis zu überprüfen

Für 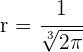 erhalten wir
erhalten wir 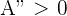
Das Kriterium der 2. Ableitung besagt also: Wenn die 2. Ableitung größer als 0 (positiv) ist, dann hat die Funktion ein relatives Minimum. Somit existiert für 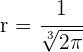 und
und 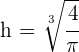 ein relatives Minimum.
ein relatives Minimum.
Man hat einen 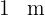 langen Draht und möchte ihn in zwei Teile teilen, um mit dem einen einen Kreis und mit dem anderen ein Quadrat zu bilden.
langen Draht und möchte ihn in zwei Teile teilen, um mit dem einen einen Kreis und mit dem anderen ein Quadrat zu bilden.
Berechne die Länge der einzelnen Teile, sodass die Summe der Flächen des Kreises und des Quadrats minimal ist.
1 Zu optimierende Funktion

2 Wir setzen die Variablen in Beziehung:
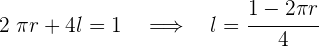
3 Wir setzen in die Funktion ein
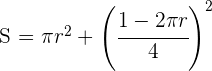
4 Wir leiten ab, setzen gleich 0 und berechnen die Nullstellen
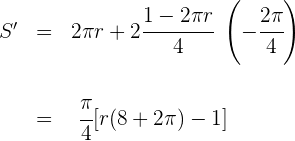
Wir setzen gleich 0 Null und berechnen die Nullstellen
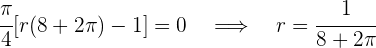
Das Stück für den Kreis misst 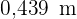 und das Stück für das Quadrat
und das Stück für das Quadrat 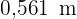
5 Wir führen die 2. Ableitung durch, um das erhaltene Ergebnis zu überprüfen
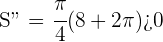
Das Kriterium der 2. Ableitung besagt also: Wenn die 2. Ableitung größer als 0 (positiv) ist, dann hat die Funktion ein relatives Minimum.
Ermittle die Maße, die die Kosten für einen rechteckigen, parallelepipedförmigen Behälter minimieren, wobei sein Volumen 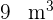 und seine Höhe
und seine Höhe 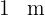 sein sollen. Die Baukosten pro
sein sollen. Die Baukosten pro  sollen bei
sollen bei  € für die Grundfläche betragen; sowie
€ für die Grundfläche betragen; sowie  € für die Abdeckung und
€ für die Abdeckung und  € pro Seitenwand.
€ pro Seitenwand.
1 Wir stellen die Werte grafisch
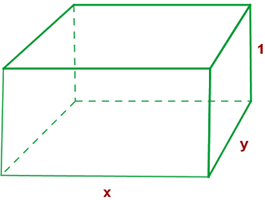
2 Zu optimierende Funktion

3 Wir setzen die Variablen in Beziehung
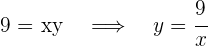
4 Wir setzen in die Funktion ein:
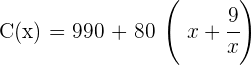
5 Wir leiten ab, setzen gleich 0 und berechnen die Nullstellen
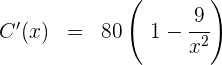
Wir setzen gleich 0 und berechnen die Nullstellen

Somit ist 
6 Wir führen die 2. Ableitung durch, um das erhaltene Ergebnis zu überprüfen
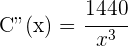
Für  erhalten wir
erhalten wir 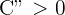
Das Kriterium der 2. Ableitung besagt also: Wenn die 2. Ableitung größer als 0 ist, dann hat die Funktion ein relatives Minimum.
Zerlege die Zahl  in zwei Summanden so, dass das Fünffache des Quadrats der ersten Zahl plus das Sechsfache des Quadrats der zweiten Zahl ein Minimum ergibt.
in zwei Summanden so, dass das Fünffache des Quadrats der ersten Zahl plus das Sechsfache des Quadrats der zweiten Zahl ein Minimum ergibt.
1 Zu optimierende Funktion

2 Wir setzen die Variablen in Verbindung:

3 Wir setzen in die Funktion ein:

4 Wir leiten ab, setzen gleich 0 und berechnen die Nullstellen
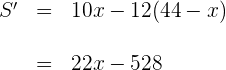
Wir setzen gleich 0 und berechnen die Nullstellen

Somit ist 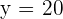
5 Wir führen die 2. Ableitung durch, um das erhaltene Ergebnis zu überprüfen
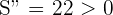
Das Kriterium der 2. Ableitung besagt also: Wenn die 2. Ableitung größer als null (positiv) ist, dann hat die Funktion ein relatives Minimum.
Aus einem Karton mit den Maßen 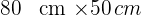 schneidet man aus jeder Ecke ein Quadrat mit der Seite
schneidet man aus jeder Ecke ein Quadrat mit der Seite  aus und faltet es (siehe Abbildung), sodass eine Box entsteht.
aus und faltet es (siehe Abbildung), sodass eine Box entsteht.
Berechne  so, dass das Volumen dieses Kartons maximal ist.
so, dass das Volumen dieses Kartons maximal ist.
1 Wir stellen die Werte grafisch dar
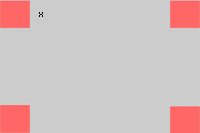
2 Zu optimierende Funktion
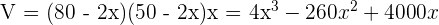
3 Wir leiten ab, setzen gleich 0 und berechnen die Nullstellen
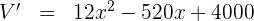
Wir setzen gleich 0 und berechnen die Nullstellen

Allerdings ist 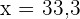 nicht gültig, da
nicht gültig, da 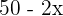
Für 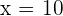 erhalten wir
erhalten wir  V''(10) < 0[/latex]
V''(10) < 0[/latex]
Das Kriterium der 2. Ableitung besagt also: Wenn die 2. Ableitung kleiner als 0 ist, dann hat die Funktion ein relatives Maximum.
Ein Blatt Papier muss 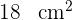 gedruckten Text, einen oberen und unteren Rand von
gedruckten Text, einen oberen und unteren Rand von  und einen seitlichen Rand von
und einen seitlichen Rand von 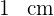 aufweisen.
aufweisen.
Bestimme die Maße, die die Fläche des Papiers so klein wie möglich halten.
1 Wir stellen die Werte grafisch dar

2 Zu optimierende Funktion

3 Wir setzen die Variablen in Beziehung:
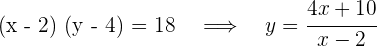
4 Wir setzen in die Funktion ein:
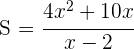
5 Wir leiten ab, setzen gleich 0 und berechnen die Nullstellen

Wir setzen gleich 0 (nur den Zähler) und berechnen die Nullstellen
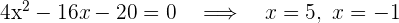
Allerdings ist  nicht gültig
nicht gültig
6 Wir führen die 2. Ableitung durch, um das erhaltene Ergebnis zu überprüfen
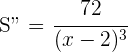
Für  erhalten wir
erhalten wir 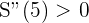
Das Kriterium der 2. Ableitung besagt also: Wenn die 2. Ableitung größer als 0 ist, dann hat die Funktion ein relatives Minimum.
Der monatliche Nettogewinn in Millionen Euro eines Unternehmens, das Busse herstellt, ist durch die folgende Funktion gegeben:
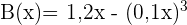 ,
,
wobei  die Anzahl der in einem Monat produzierten Busse ist.
die Anzahl der in einem Monat produzierten Busse ist.
1 Berechne die monatliche Produktion, die den Gewinn maximiert.
2 Der maximale Gewinn entspricht dieser Produktion.
1 Zu optimierende Funktion
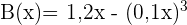
2 Wir leiten ab, setzen gleich 0 und berechnen die Nullstellen
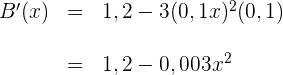
Wir setzen gleich 0 und berechnen die Nullstellen
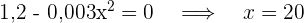
3 Wir führen die 2. Ableitung durch, um das erhaltene Ergebnis zu überprüfen.
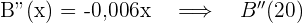
Eine Obstplantage hat  Bäume, die jeweils
Bäume, die jeweils  Früchte produieren.
Früchte produieren.
Es wird geschätzt, dass für jeden zusätzlich gepflanzten Baum die Produktion eines jeden Baumes um  Früchte abnimmt.
Früchte abnimmt.
Berechne:
1 Die aktuelle Produktion der Obstplantage.
2 Die Produktion, die von jedem Baum erzielt werden würde, wenn  mehr Bäume gepflanzt würden.
mehr Bäume gepflanzt würden.
3 Die Gesamterzeugung der Obstplantage, wenn  mehr Bäume gepflanzt würden.
mehr Bäume gepflanzt würden.
4 Wie hoch sollte die Gesamtzahl der Bäume in der Obstplantage sein, um eine maximale Produktion zu erzielen?
1 Die aktuelle Produktion der Obstplantage.
Aktuelle Produktion: 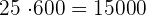 Früchte.
Früchte.
2 Die Produktion, die von jedem Baum erzielt werden würde, wenn  mehr Bäume gepflanzt würden.
mehr Bäume gepflanzt würden.
Wenn  mehr Bäume gepflanzt werden, beläuft sich die Produktion jedes Baumes:
mehr Bäume gepflanzt werden, beläuft sich die Produktion jedes Baumes:  .
.
3 Die Gesamterzeugung der Obstplantage, wenn  mehr Bäume gepflanzt würden.
mehr Bäume gepflanzt würden.
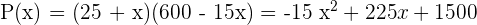
4 Wie hoch sollte die Gesamtzahl der Bäume in der Obstplantage sein, um eine maximale Produktion zu erzielen?
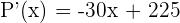
Wir setzen die Ableitung gleich 0

Wir berechnen die 2. Ableitung
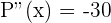 oder
oder 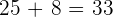 Bäume hat.
Bäume hat.
Mit KI zusammenfassen:


