Kapitel

Wie ermittelt man die einzelnen Elemente einer Parabel?
Gegeben sei die Parabel 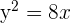 . Berechne ihren Scheitelpunkt, ihren Brennpunkt sowie ihre Leitlinie.
. Berechne ihren Scheitelpunkt, ihren Brennpunkt sowie ihre Leitlinie.
Berechne zuerst den Parameter p, der den Abstand zwischen dem Brennpunkt und der Leitlinie der Parabel angibt. Der Parameter p ist:

Es handelt sich um eine Normalparabel, das heißt ihr Scheitelpunkt liegt im Koordinatenursprung

Der quadratische Term der Gleichung ist  , d.h. die Parabelachse (die Symmetrieachse, die durch den Scheitelpunkt verläuft) entspricht der x-Achse. Da der Koeffizient der nicht quadratischen Variable
, d.h. die Parabelachse (die Symmetrieachse, die durch den Scheitelpunkt verläuft) entspricht der x-Achse. Da der Koeffizient der nicht quadratischen Variable  ) positiv ist (8), liegt die Parabel im positiven Teil der x-Achse
) positiv ist (8), liegt die Parabel im positiven Teil der x-Achse
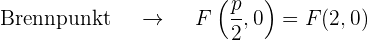
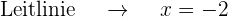
Grafisch sieht die Parabel 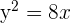 so aus:
so aus:
Gegeben sei die Parabel 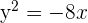 . Berechne ihren Scheitelpunkt, ihren Brennpunkt sowie ihre Leitlinie.
. Berechne ihren Scheitelpunkt, ihren Brennpunkt sowie ihre Leitlinie.
Berechne zuerst den Parameter p, der den Abstand zwischen dem Brennpunkt und der Leitlinie der Parabel angibt. Der Parameter p ist:

Es handelt sich um eine Normalparabel, das heißt ihr Scheitelpunkt liegt im Koordinatenursprung

Der quadratische Term der Gleichung ist  , d.h. die Parabelachse (die Symmetrieachse, die durch den Scheitelpunkt verläuft) entspricht der x-Achse. Da der Koeffizient der nicht quadratischen Variable
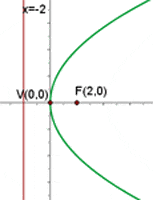
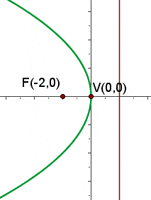
, d.h. die Parabelachse (die Symmetrieachse, die durch den Scheitelpunkt verläuft) entspricht der x-Achse. Da der Koeffizient der nicht quadratischen Variable  ) negativ ist (-8), liegt die Parabel im negativen Teil der x-Achse
) negativ ist (-8), liegt die Parabel im negativen Teil der x-Achse
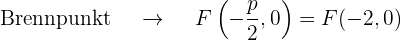
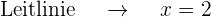
Grafisch sieht die Parabel 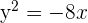 so aus:
so aus:
Gegeben sei die Parabel 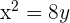 . Berechne ihren Scheitelpunkt, ihren Brennpunkt sowie ihre Leitlinie.
. Berechne ihren Scheitelpunkt, ihren Brennpunkt sowie ihre Leitlinie.
Berechne zuerst den Parameter p, der den Abstand zwischen dem Brennpunkt und der Leitlinie der Parabel angibt. Der Parameter p ist:

Es handelt sich um eine Normalparabel, das heißt ihr Scheitelpunkt liegt im Koordinatenursprung

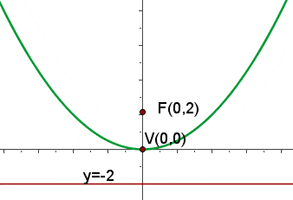
Der quadratische Term der Gleichung ist  , d.h. die Parabelachse verläuft entlang der y-Achse. Da der Koeffizient der nicht quadratischen Variable
, d.h. die Parabelachse verläuft entlang der y-Achse. Da der Koeffizient der nicht quadratischen Variable  ) positiv ist (8), liegt die Parabel im positiven Teil der y-Achse
) positiv ist (8), liegt die Parabel im positiven Teil der y-Achse
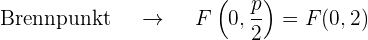
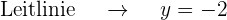
Grafisch sieht die Parabel 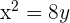 so aus:
so aus:
Gegeben sei die Parabel 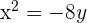 . Berechne ihren Scheitelpunkt, ihren Brennpunkt sowie ihre Leitlinie.
. Berechne ihren Scheitelpunkt, ihren Brennpunkt sowie ihre Leitlinie.
Berechne zuerst den Parameter p, der den Abstand zwischen dem Brennpunkt und der Leitlinie der Parabel angibt. Der Parameter p ist:

Es handelt sich um eine Normalparabel, das heißt ihr Scheitelpunkt liegt im Koordinatenursprung

Der quadratische Term der Gleichung ist  , d.h. die Parabelachse verläuft entlang der y-Achse. Da der Koeffizient der nicht quadratischen Variable
, d.h. die Parabelachse verläuft entlang der y-Achse. Da der Koeffizient der nicht quadratischen Variable  ) negativ ist (-8), liegt die Parabel im negativen Teil der y-Achse
) negativ ist (-8), liegt die Parabel im negativen Teil der y-Achse
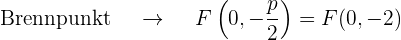
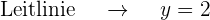
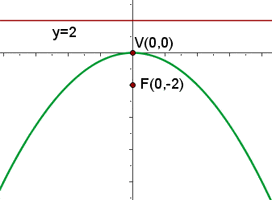
Grafisch sieht die Parabel 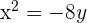 so aus
so aus
Gegeben sei die Parabel 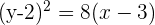 . Berechne ihren Scheitelpunkt, ihren Brennpunkt sowie ihre Leitlinie.
. Berechne ihren Scheitelpunkt, ihren Brennpunkt sowie ihre Leitlinie.
Berechne zuerst den Parameter p, der den Abstand zwischen dem Brennpunkt und der Leitlinie der Parabel angibt. Der Parameter p ist:

Hier liegt keine Normalparabel vor, daher liegt der Scheitelpunkt bei

Der quadratische Term der Gleichung ist  , d.h. die Parabelachse verläuft parallel zur x-Achse. Da der Koeffizient der nicht quadratischen Variable
, d.h. die Parabelachse verläuft parallel zur x-Achse. Da der Koeffizient der nicht quadratischen Variable  ) positiv ist (8), liegt der Brennpunkt rechts vom Scheitelpunkt.
) positiv ist (8), liegt der Brennpunkt rechts vom Scheitelpunkt.
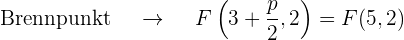
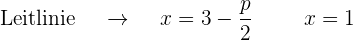
Grafisch sieht die Parabel 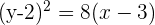 so aus:
so aus:
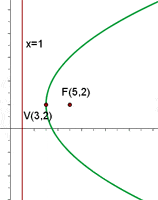
Gegeben sei die Parabel 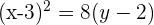 . Ermittle ihren Scheitelpunkt, ihren Brennpunkt und ihre Leitlinie.
. Ermittle ihren Scheitelpunkt, ihren Brennpunkt und ihre Leitlinie.
Berechne zuerst den Parameter p, der den Abstand zwischen dem Brennpunkt und der Leitlinie der Parabel angibt. Der Parameter p ist:

Hier liegt keine Normalparabel vor, daher liegt der Scheitelpunkt bei

Der quadratische Term der Gleichung ist  , d.h. die Parabelachse verläuft parallel zur x-Achse. Da der Koeffizient der nicht quadratischen Variable
, d.h. die Parabelachse verläuft parallel zur x-Achse. Da der Koeffizient der nicht quadratischen Variable  ) positiv ist (8), liegt der Brennpunkt rechts vom Scheitelpunkt.
) positiv ist (8), liegt der Brennpunkt rechts vom Scheitelpunkt.
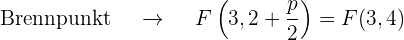
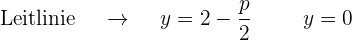
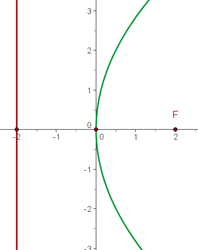
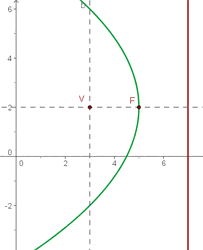
Grafisch sieht die Parabel 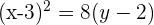 so aus:
so aus:
Stelle die Gleichungen der folgenden Parabeln in vereinfachter Form dar und gib den Wert des Parameters p, die Koordinaten des Brennpunkts sowie die Gleichung der Leitlinie an.



1  Löse nach
Löse nach  auf
auf


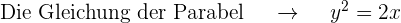
Berechne zuerst den Parameter p, der den Abstand zwischen dem Brennpunkt und der Leitlinie der Parabel angibt. Der Parameter p ist:

Es handelt sich um eine Normalparabel, das heißt ihr Scheitelpunkt liegt im Koordinatenursprung

Der quadratische Term der Gleichung ist  , d.h. die Parabelachse (die Symmetrieachse, die durch den Scheitelpunkt verläuft) entspricht der x-Achse. Da der Koeffizient der nicht quadratischen Variable
, d.h. die Parabelachse (die Symmetrieachse, die durch den Scheitelpunkt verläuft) entspricht der x-Achse. Da der Koeffizient der nicht quadratischen Variable  ) positiv ist (2), liegt der Brennpunkt rechts vom Scheitelpunkt.
) positiv ist (2), liegt der Brennpunkt rechts vom Scheitelpunkt.
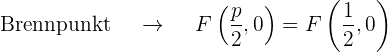
Grafisch sieht die Parabel  so aus:
so aus:
2 
Löse nach  auf
auf


Berechne zuerst den Parameter p, der den Abstand zwischen dem Brennpunkt und der Leitlinie der Parabel angibt. Der Parameter p ist:

Es handelt sich um eine Normalparabel, das heißt ihr Scheitelpunkt liegt im Koordinatenursprung

Der quadratische Term der Gleichung ist  , d.h. die Parabelachse (die Symmetrieachse, die durch den Scheitelpunkt verläuft) entspricht der x-Achse. Da der Koeffizient der nicht quadratischen Variable
, d.h. die Parabelachse (die Symmetrieachse, die durch den Scheitelpunkt verläuft) entspricht der x-Achse. Da der Koeffizient der nicht quadratischen Variable  ) negativ ist (
) negativ ist ( 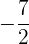 ), liegt der Brennpunkt links vom Scheitelpunkt.
), liegt der Brennpunkt links vom Scheitelpunkt.
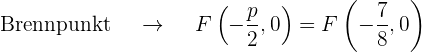
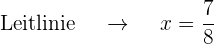
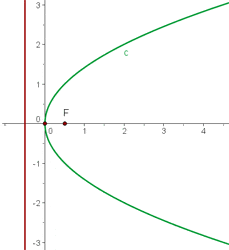
Grafisch sieht die Parabel  so aus:
so aus:
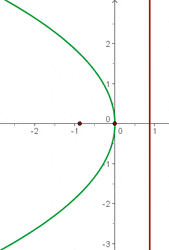
3 
Löse nach  auf
auf


Berechne zuerst den Parameter p, der den Abstand zwischen dem Brennpunkt und der Leitlinie der Parabel angibt. Der Parameter p ist:

Es handelt sich um eine Normalparabel, das heißt ihr Scheitelpunkt liegt im Koordinatenursprung

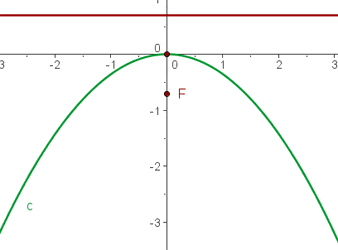
Der quadratische Term der Gleichung ist  , d.h. die Parabelachse verläuft entlang der y-Achse. Da der Koeffizient der nicht quadratischen Variable
, d.h. die Parabelachse verläuft entlang der y-Achse. Da der Koeffizient der nicht quadratischen Variable  ) negativ ist (
) negativ ist ( 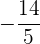 ), liegt der Brennpunkt unterhalb des Scheitelpunkts.
), liegt der Brennpunkt unterhalb des Scheitelpunkts.
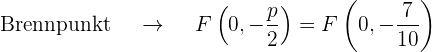
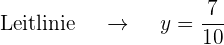
Grafisch sieht die Parabel 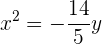 so aus:
so aus:
Ermittle die Koordinaten des Scheitelpunkts, der Brenpunkte und die Gleichungen der Leitlinien der folgenden Parabeln:



Ermittle die Koordinaten des Scheitelpunkts, der Brenpunkte und die Gleichungen der Leitlinien der folgenden Parabeln:
1 
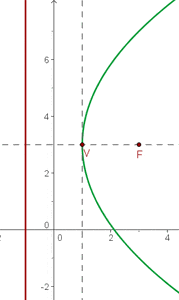
Fasse die quadratische Gleichung zusammen

Vereinfache
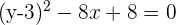
Löse auf
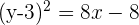


Der Parameter p ist:

Der quadratische Term der Gleichung ist  , d.h. die Parabelachse verläuft parallel zur x-Achse. Da der Koeffizient der nicht quadratischen Variable
, d.h. die Parabelachse verläuft parallel zur x-Achse. Da der Koeffizient der nicht quadratischen Variable  ) positiv ist (8), liegt der Brennpunkt rechts vom Scheitelpunkt.
) positiv ist (8), liegt der Brennpunkt rechts vom Scheitelpunkt.
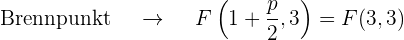
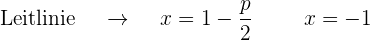
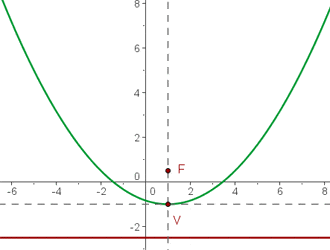
Fasse die quadratische Gleichung zusammen

Vereinfache

Löse auf
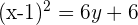

Folglich ist

Der Parameter p ist:

Der quadratische Term der Gleichung ist  , d.h. die Parabelachse verläuft entlang der y-Achse. Da der Koeffizient der nicht quadratischen Variable
, d.h. die Parabelachse verläuft entlang der y-Achse. Da der Koeffizient der nicht quadratischen Variable  ) positiv ist (6), liegt der Brennpunkt oberhalb des Scheitelpunkts.
) positiv ist (6), liegt der Brennpunkt oberhalb des Scheitelpunkts.
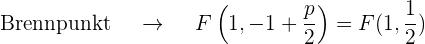
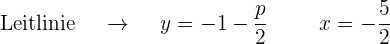
3 
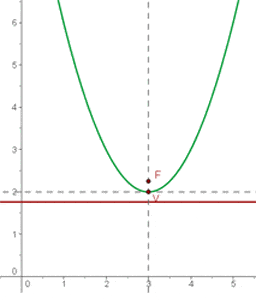
Fasse die quadratische Gleichung zusammen

Vereinfache
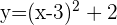
Löse auf
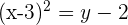

Berechne zuerst den Parameter p, der den Abstand zwischen dem Brennpunkt und der Leitlinie der Parabel angibt. Der Parameter p ist:

Der quadratische Term der Gleichung ist  , d.h. die Parabelachse verläuft entlang der y-Achse. Da der Koeffizient der nicht quadratischen Variable
, d.h. die Parabelachse verläuft entlang der y-Achse. Da der Koeffizient der nicht quadratischen Variable  ) positiv ist (1), liegt der Brennpunkt oberhalb des Scheitelpunkts.
) positiv ist (1), liegt der Brennpunkt oberhalb des Scheitelpunkts.
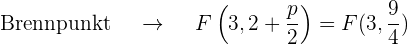
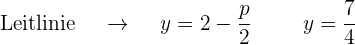
Wie stellt man Parabelgleichungen auf?
Stelle anhand der folgenden Parameter die jeweilige Parabelgleichung auf:
Leitlinie  , Brennpunkt
, Brennpunkt 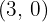 .
.
Leitlinie  , Scheitelpunkt
, Scheitelpunkt  .
.
Leitlinie 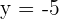 , Brennpunkt
, Brennpunkt  .
.
Leitlinie  , Brennpunkt
, Brennpunkt 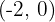 .
.
Brennpunkt  , Scheitelpunkt
, Scheitelpunkt  .
.
Brennpunkt 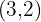 , Scheitelpunkt
, Scheitelpunkt 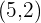 .
.
Brennpunkt 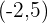 , Scheitelpunkt
, Scheitelpunkt 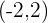 .
.
Brennpunkt  , Scheitelpunkt
, Scheitelpunkt 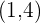 .
.
Stelle die Gleichungen der Parabeln anhand der vorgegebenen Werte auf:
1
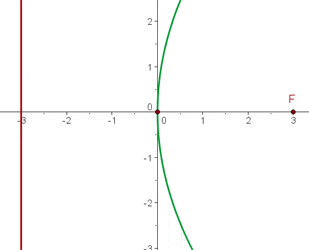
Berechne zuerst den Abstand zwischen dem Brennpunkt und der Leitlinie, um den Parameter  zu erhalten.
zu erhalten.

Da der Brennpunkt auf der x-Achse liegt, die Leitlinie parallel zur y-Achse verläuft und beide den selben Abstand zum Koordinatenursprung aufweisen, handelt es sich um eine Normalparabel.

Da die Parabelachse entlang der x-Achse verläuft und der Brennpunkt rechts vom Scheitelpunkt liegt, ist die Gleichung

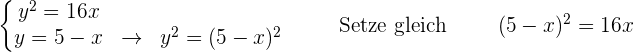
Vereinfache


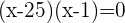
Löse auf

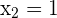
2
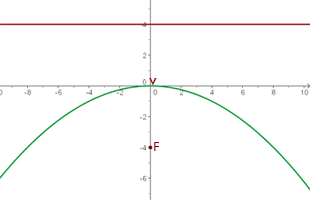
Berechne zuerst den Abstand vom Scheitelpunkt zur Leitlinie. Dieser ist 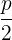 .
.

Man kann erkennen, dass der Scheitelpunkt auf dem Koordinatenursprung liegt und die Leitlinie parallel zur x-Achse verläuft. Folglich liegt eine Normalparabel vor.
Da die Parabelachse entlang der y-Achse verläuft und der Brennpunkt unterhalb des Scheitelpunkts liegt, ergibt sich als Gleichung
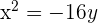
3 Berechne zuerst den Abstand zwischen dem Brennpunkt und der Leitlinie, um den Parameter Man kann erkennen, dass die Leitlinie parallel zur x-Achse verläuft und der Brennpunkt auf der y-Achse liegt. Beide sind vom Koordinatenursprung gleich weit entfernt, folglich liegt wieder eine Normalparabel vor. Da der Brennpunkt oberhalb der Leitlinie liegt, ergibt sich als Gleichung 4 Berechne zuerst den Abstand zwischen dem Brennpunkt und der Leitlinie, um den Parameter Man kann erkennen, dass die Leitlinie parallel zur y-Achse verläuft und der Brennpunkt auf der x-Achse liegt. Beide sind vom Koordinatenursprung gleich weit entfernt, folglich liegt wieder eine Normalparabel vor. Da der Brennpunkt links von der Leitlinie liegt, ergibt sich als Gleichung 5 Berechne zuerst den Abstand zwischen dem Brennpunkt und der Leitlinie, um den Parameter Man kann erkennen, dass die Leitlinie parallel zur y-Achse verläuft und der Brennpunkt auf der x-Achse liegt. Beide sind vom Koordinatenursprung gleich weit entfernt, folglich liegt wieder eine Normalparabel vor. a der Brennpunkt rechts von der Leitlinie liegt, ergibt sich als Gleichung 6 Berechne zuerst den Abstand vom Brennpunkt zur Leitlinie. Dieser ist Man erkennt, dass die Leitlinie parallel zur y-Achse verläuft. Da der Brennpunkt links des Scheitelpunkts liegt, ergibt sich als Gleichung 7 Berechne zuerst den Abstand vom Brennpunkt zum Scheitelpunkt. Dieser ist Mann erkennt, dass die Leitlinie Da der Brennpunkt oberhalb des Scheitelpunkts liegt, ergibt sich als Gleichung 8 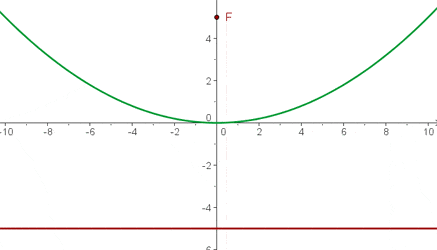
 zu erhalten.
zu erhalten.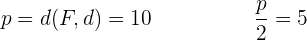
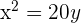
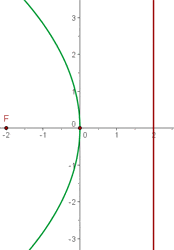
 zu erhalten.
zu erhalten.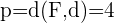
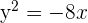
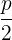 zu erhalten.
zu erhalten.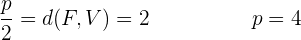
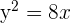
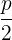 .
.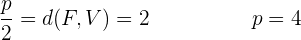
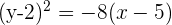
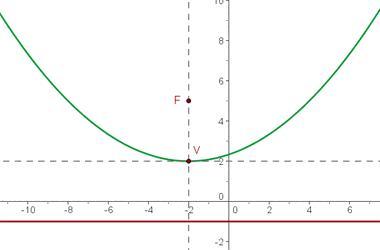
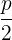 .
.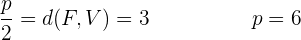
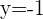 parallel zur x-Achse verläuft.
parallel zur x-Achse verläuft.
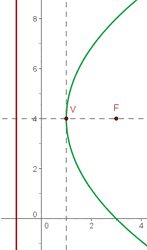
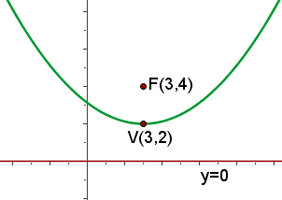
Bestimme die Gleichung einer Parabel, deren Scheitelpunkt im Koordinatenursprung liegt und deren Hauptachse entlang der x-Achse verläuft unter Beachtung, dass der Punkt  auf der Parabel liegt.
auf der Parabel liegt.
Da der Scheitelpunkt der Parabel im Koordinatenursprung liegt und ihre Achse entlang der x-Achse verläuft, handelt es sich um eine Normalparabel, genauer gesagt um die Parabel der Form

Da die Parabelkurve durch den Punkt (3,4) verläuft, muss die Gleichung bei Einsetzen der Koordinaten aufgehen
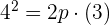
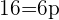
Teile durch 3

Die Gleichung sieht folglich so aus:
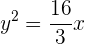
Bestimme die Gleichung einer Parabel, deren Hauptachse parallel zur y-Achse verläuft. Ihr Scheitelpunkt liegt auf der x-Achse und sie verläuft durch die Punkte  und
und 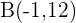 .
.
Aus der Rechenaufgabe geht hervor, dass
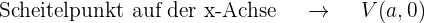

Da die Parabelkurve durch die Punkte A und B verläuft, muss die Gleichung für diese Koordinaten aufgehen:
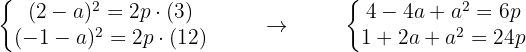
Multiliziere die erste Gleichung mit 4 und du erhältst:

Ziehe von ihr die zweite Gleichung ab, indem du die negative Form zu ihr addierst

Somit erhältst du


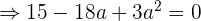
Vereinfache die Gleichung, indem du sie durch 3 teilst
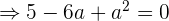
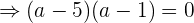
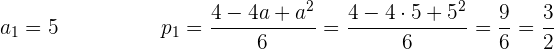

Die beiden Lösungen für  lassen erkennen, dass hier Lösungen für zwei unterschiedliche Parabeln vorliegen:
lassen erkennen, dass hier Lösungen für zwei unterschiedliche Parabeln vorliegen:

Bestimme die Gleichung der Parabel mit Leitlinie 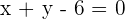 , deren Brennpunkt im Koordinatenursprung liegt.
, deren Brennpunkt im Koordinatenursprung liegt.
Der Abstand von einem Punkt 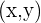 zur Leitlinie muss gleich groß sein wie zum Brennpunkt. Folglich ist
zur Leitlinie muss gleich groß sein wie zum Brennpunkt. Folglich ist 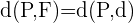

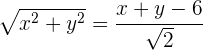
Quadriere den Ausdruck, um die Wurzel aufzulösen
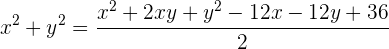
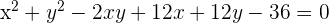
Bestimme die Gleichung einer Parabel mit vertikaler Hauptachse, die durch die Punkte 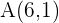 ,
, 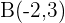 und
und  verläuft.
verläuft.
Die GLeichung muss folgende Form besitzen: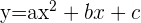
Da die Parabel durch die Punkte A, B und C verläuft, muss die Gleichung bei Einsetzen der Koordinaten aufgehen
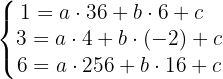
Löse das Gleichungssystem mit 3 Unbekannten und du erhältst
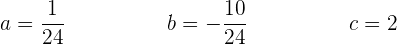
Folglich ist die Parabelgleichung

Bestimme die Gleichung der Parabel mit Leitlinie  und Brennpunkt
und Brennpunkt  .
.
Bestimme die Gleichung der Parabel mit Leitlinie y = 0 und Brennpunkt (2, 4).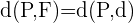
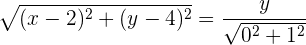
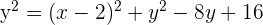
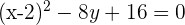
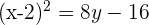
Folglich ist die Parabelgleichung:

Bestimme die Lagebeziehung der Geraden  zur Parabel
zur Parabel 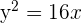 .
.
Bestimme die Lagebeziehung der Geraden r ≡ x + y − 5 = 0 zur Parabel y² = 16 x.
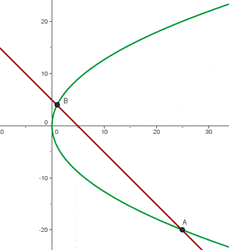
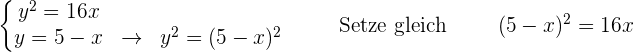
Vereinfache


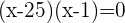
Löse auf

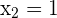
Mit KI zusammenfassen:













