Kapitel

Wiederholung
Anhand der kanonischen Parabelgleichung können die einzelnen Elemente einer Parabel problemlos ermittelt werden. Genauso leicht lässt sich eine Parabelgleichung mithilfe von vorgegebenen Parametern aufstellen.
In diesem Artikel haben wir alles, was du über Parabeln wissen solltest, für dich zusammengefasst
Die kanonische Parabelgleichung:
1 
Die Parabel ist nach rechts geöffnet
Brennpunkt 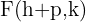
Leitlinie 
2 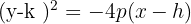
Die Parabel ist nach links geöffnet
Brennpunkt 
Leitlinie 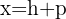
3 
Die Parabel ist nach oben geöffnet
Brennpunkt 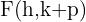
Leitlinie 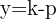
4 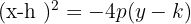
Die Parabel ist nach unten geöffnet
Brennpunkt 
Leitlinie 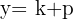
Der Punkt 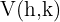 ist der Scheitelpunkt der Parabel.
ist der Scheitelpunkt der Parabel.
Wenn der Scheitelpunkt der Parabel im Koordinatenursprung liegt, bedeutet das für die Gleichung folgendes:
1 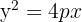
Die Parabel ist nach rechts geöffnet
Brennpunkt 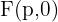
Leitlinie 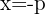
2 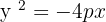
Die Parabel ist nach links geöffnet
Brennpunkt 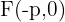
Leitlinie 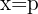
3 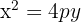
Die Parabel ist nach oben geöffnet
Brennpunkt 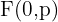
Leitlinie 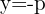
4 
Die Parabel ist nach unten geöffnet
Brennpunkt 
Leitlinie 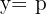
 gibt die Länge der geraden Seite (LR) an.
gibt die Länge der geraden Seite (LR) an.
Dabei ist  der Abstand vom Scheitelpunkt zum Brennpunkt und vom Scheitelpunkt zur Leitlinie.
der Abstand vom Scheitelpunkt zum Brennpunkt und vom Scheitelpunkt zur Leitlinie.
Aufgaben
Berechne anhand der folgenden Parabelgleichungen ihren jeweiligen Brennpunkt , die Gleichungen ihrer Leitlinien, die Abstände zu ihren geraden Seiten und stelle sie anschließend grafisch dar.



Bestimme zum Aufstellen der Parabelgleichung zuerst den Wert des Parameters  und anhand dessen die Koordinaten des Brennpunkts sowie die Gleichung der Leitlinie.
und anhand dessen die Koordinaten des Brennpunkts sowie die Gleichung der Leitlinie.
1 
Löse die quadratische Gelichung

Bestimme den Wert von p

Bestimme den Brennpunkt und ermittle anhand dessen die Leitlinie
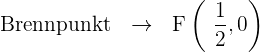
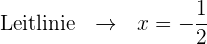
Stelle die Parabel mithilfe der erhaltenen Informationen grafisch dar
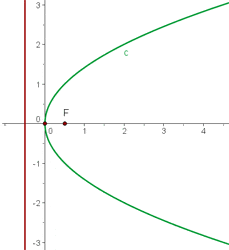
2 
Löse die quadratische Gleichung

Bestimme den Wert von p

Bestimme den Brennpunkt und ermittle anhand dessen die Leitlinie
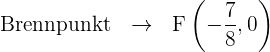
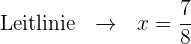
Stelle die Parabel mithilfe der erhaltenen Informationen grafisch dar
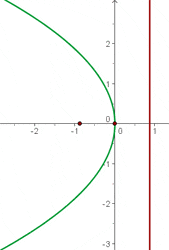
3 
Löse die quadratische Gleichung

Bestimme den Wert von p

Bestimme den Brennpunkt und ermittle anhand dessen die Leitlinie
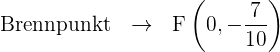
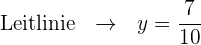
Stelle die Parabel mithilfe der erhaltenen Informationen grafisch dar
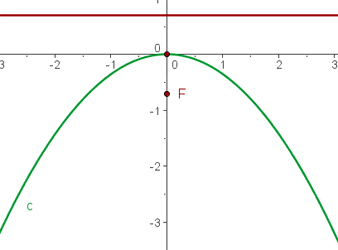
Ermittle die Koordinaten des Scheitelpunkts und des Brennpunkts sowie die Gleichung der Leitlinie der folgenden Parabeln:



Bestimme zum Aufstellen der Parabelgleichung zuerst den Wert des Parameters  und anhand dessen die Koordinaten des Brennpunkts und des Scheitelpunkts.
und anhand dessen die Koordinaten des Brennpunkts und des Scheitelpunkts.
1 
Vervollständige die Gleichung, um ein perfektes quadratisches Trinom zu erhalten und löse auf


Faktorisiere

Bestimme die Elemente der Parabel anhand der Gleichung
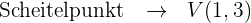
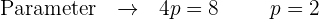
Berechne anhand des Scheitelpunkts und des Parameters  den Brennpunkt und die Leitlinie
den Brennpunkt und die Leitlinie
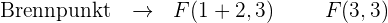
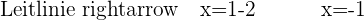
Stelle die Parabel anhand der ermittelten Werte im Koordinatensystem grafisch dar
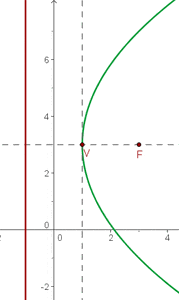
2 
Vervollständige die Gleichung, um ein perfektes quadratisches Trinom zu erhalten und löse auf


Faktorisiere

Bestimme die Elemente der Parabel anhand der Gleichung

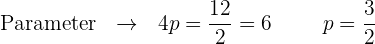
Berechne anhand des Scheitelpunkts und des Parameters  den Brennpunkt und die Leitlinie
den Brennpunkt und die Leitlinie
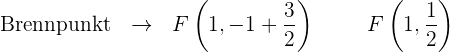
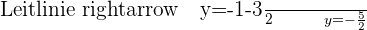
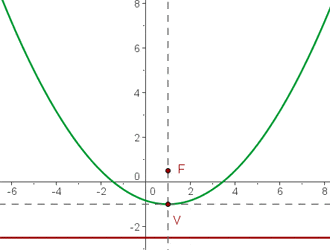
Stelle die Parabel anhand der ermittelten Werte im Koordinatensystem grafisch dar
3 
Vervollständige die Gleichung, um ein perfektes quadratisches Trinom zu erhalten und löse auf


Faktorisiere

Bestimme die Elemente der Parabel anhand der Gleichung
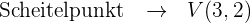
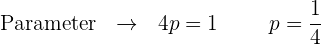
Berechne anhand des Scheitelpunkts und des Parameters  den Brennpunkt und die Leitlinie
den Brennpunkt und die Leitlinie
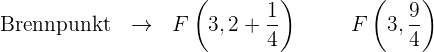
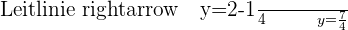
Stelle die Parabel anhand der ermittelten Werte im Koordinatensystem grafisch dar
Stelle anhand der folgenden Werte die zugehörige Parabelgleichung auf:
Leitlinie  , Brennpunkt
, Brennpunkt 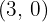 .
.
Leitlinie 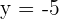 , Brennpunkt
, Brennpunkt  .
.
Leitlinie  , Brennpunkt
, Brennpunkt 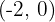 .
.
Leitlinie  , Scheitelpunkt
, Scheitelpunkt  .
.
1 Leitlinie  , Brennpunkt
, Brennpunkt 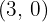 .
.
Anhand der Lage der Leitlinie und des Brennpunkts lässt sich ableiten, dass die Parabel nach rechts geöffnet ist und ihr Scheitelpunkt im Koordinatenursprung liegt.
Wir wissen, dass der Brennpunkt dieser Parabeln die Koordinaten 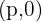 besitzt, folglich ist
besitzt, folglich ist
 .
.
Die Gleichung lautet
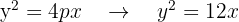
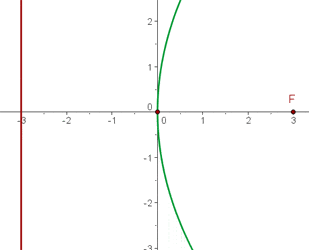
2 Leitlinie y = -5, Brennpunkt (0, 5).
Anhand der Lage der Leitlinie und des Brennpunkts lässt sich ableiten, dass die Parabel nach links geöffnet ist und ihr Scheitelpunkt im Koordinatenursprung liegt.
Wir wissen, dass der Brennpunkt dieser Parabeln die Koordinaten 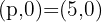 besitzt, folglich ist
besitzt, folglich ist
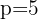 .
.
Setze den Wert in die Gleichung ein:

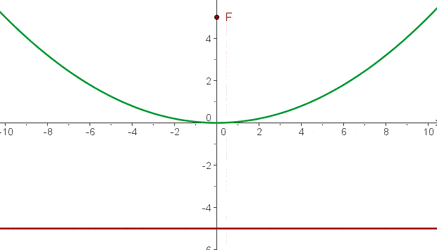
3 Leitlinie  , Brennpunkt
, Brennpunkt 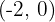 .
.
Anhand der Lage der Leitlinie und des Brennpunkts lässt sich ableiten, dass die Parabel nach links geöffnet ist und ihr Scheitelpunkt im Koordinatenursprung liegt.
Wir wissen, dass der Brennpunkt der Parabeln mit Öffnung nach links 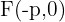 ist, das heißt
ist, das heißt

Setze den Wert in die Gleichung ein:
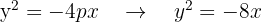
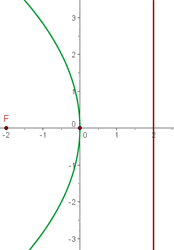
4 Leitlinie  , Scheitelpunkt
, Scheitelpunkt  .
.
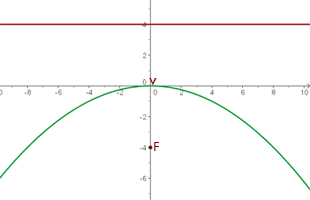
Anhand der Lage der Leitlinie und des Brennpunkts lässt sich ableiten, dass die Parabel nach unten geöffnet ist und ihr Scheitelpunkt im Koordinatenursprung liegt.
Für diese Art von Parabeln ist die Leitlinie  . Folglich ist
. Folglich ist

Die Gleichung besitzt die Form:

Stelle die Parabelgleichungen anhand des Brennpunkts und Scheitelpunkts auf.
Brennpunkt  , Scheitelpunkt
, Scheitelpunkt  .
.
Brennpunkt 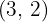 , Scheitelpunkt
, Scheitelpunkt 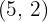 .
.
Brennpunkt 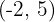 , Scheitelpunkt
, Scheitelpunkt  .
.
Brennpunkt  , Scheitelpunkt
, Scheitelpunkt 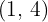 .
.
1 Brennpunkt  , Scheitelpunkt
, Scheitelpunkt  .
.
Anhand der Lage des Brennpunkts und des Scheitelpunkts lässt sich ableiten, dass die Parabel nach rechts geöffnet ist und ihr Scheitelpunkt im Koordinatenursprung liegt.
Die Gleichung hat folglich die Form

Für diese Art von Parabel ist der Brennpunkt 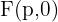 , das heißt
, das heißt

Die Parabelgleichung hat die Form:

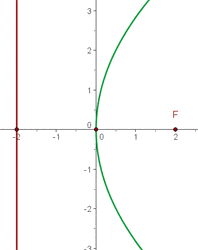
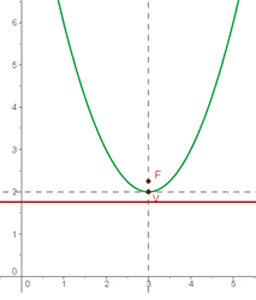
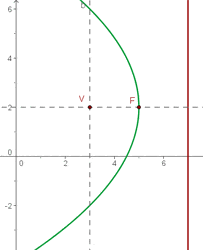
2 Brennpunkt (3, 2), Scheitelpunkt (5, 2).
Durch Einzeichnen des Brennpunkts und des Scheitelpunkts ins Koordinatensystem kann man sehen, dass der Brennpunkt links vom Scheitelpunkt liegt, daher ist die Parabel nach links geöffnet und ihre Gleichung besitzt die Form:
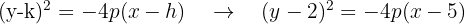
Berechne den Abstand vom Scheitelpunkt zum Brennpunkt und du erhältst

Setze den Wert in die Gleichung ein:
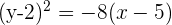
3 Brennpunkt (-2, 5), Scheitelpunkt (-2, 2).
Durch Einzeichnen des Brennpunkts und des Scheitelpunkts ins Koordinatensystem kann man sehen, dass der Brennpunkt oberhalb vom Scheitelpunkt liegt, daher ist die Parabel nach oben geöffnet und ihre Gleichung besitzt die Form:
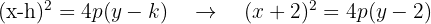
Berechne den Abstand vom Scheitelpunkt zum Brennpunkt und du erhältst

Setze den Wert in die Gleichung ein:

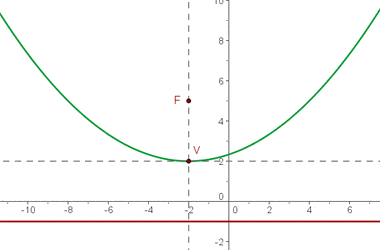
4 Brennpunkt (3, 4), Scheitelpunkt (1, 4).
Durch Einzeichnen des Brennpunkts und des Scheitelpunkts ins Koordinatensystem kann man sehen, dass der Brennpunkt rechts vom Scheitelpunkt liegt, daher ist die Parabel nach rechts geöffnet und ihre Gleichung besitzt die Form:
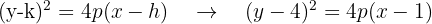
Berechne den Abstand vom Scheitelpunkt zum Brennpunkt und du erhältst

Setze den Wert in die Gleichung ein:
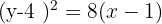
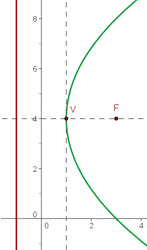
Stelle die Gleichung für eine Parabel auf, deren Leitlinie die Gerade  ist und deren Brennpunkt bei
ist und deren Brennpunkt bei  liegt.
liegt.
Wir wissen, dass der Abstand zwischen Scheitelpunkt und Brennpunkt gleich dem Abstand zwischen Scheitelpunkt und Leitlinie ist.

Der Abstand von einer Geraden  zu einem Punkt
zu einem Punkt  ist gegeben durch
ist gegeben durch
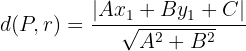
Wenn man den Scheitelpunkt als unbekannten Punkt 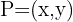 definiert, erhält man als erste Gleichung
definiert, erhält man als erste Gleichung
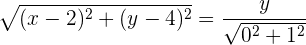
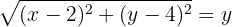
Quadriere die Gleichung, um die Wurzel auf der linken Seite aufzuheben und vereinfache


Löse auf und stelle alle Terme mit der Variablen  auf eine Seite und alle Terme mit der Variablen
auf eine Seite und alle Terme mit der Variablen  auf die andere
auf die andere
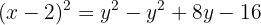
Faktorisiere

Stelle die Gleichung für eine Parabel mit vertikeler Hauptachse auf, die durch die folgenden drei Punkte verläuft:

Die allgemeine Gleichung einer Parabel mit vertikaler Hauptachse besitzt die Form
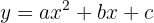
Da die Punkte A, B und C auf der Parabel liegen, geht die Gleichung bei Einsetzen der Werte auf
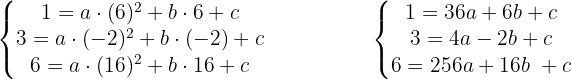
Löse das lineare Gleichungssystem und du erhältst
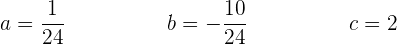
Die Parabelgleichung ist daher
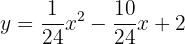
Ermittle die Lagebeziehung der Geraden 
zur Parabel 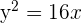 .
.
Um die Lagebeziehung zu bestimmen, prüft man zuerst, ob sich die beiden Elemente schneiden. Sollten Schnittpunkte vorliegen, würde die Parabelgleichung bei Einsetzen dieser aufgehen.
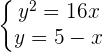
Um das Gleichungssystem zu lösen quadriert man die zweite Gleichung und setzt die Terme für  aus beiden Gleichungen miteinander gleich.
aus beiden Gleichungen miteinander gleich.

Vereinfache

Löse die quadratische Gleichung mithilfe der allgemeinen Formel.

Du erhältst die Koordinaten der  -Achse. Um die Koordinaten der
-Achse. Um die Koordinaten der  -Achse herauszufinden, setze die Werte von x in eine der Gleichungen ein. In diesem Fall ist die einfachste Art
-Achse herauszufinden, setze die Werte von x in eine der Gleichungen ein. In diesem Fall ist die einfachste Art
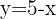
Daher ist

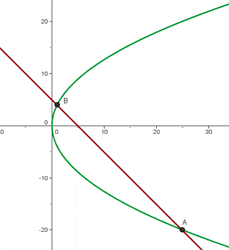
Die Schnittpunkte sind also:

Die Gerade ist daher eine Sekante zur Parabel, da sie zwei Schnittpunkte mit ihr gemeinsam hat
Mit KI zusammenfassen:













