Unter der Annahme, dass die Börse jeden Tag eines Monats mit 
Tagen arbeitet, entspricht die Notierung der Sitzungen eines bestimmten Unternehmens dem folgenden Gesetz:
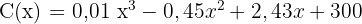
1 Ermittle die Höchst- und Mindestbeiträge sowie die Tage, an denen sie angefallen sind, an anderen Tagen als dem ersten und letzten.
2 Bestimme die Zeiträume, in denen die Aktien gestiegen oder gefallen sind.
1 Ermittle die Höchst- und Mindestbeträge sowie die Tage, an denen sie angefallen sind, an anderen Tagen als dem ersten und letzten.
Wir leiten ab
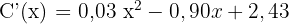
Wir setzen die Ableitung gleich 0 und ermitteln die Nullstellen der Gleichung
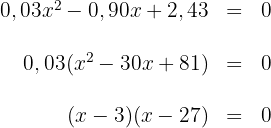
Die Nullstellen sind 
und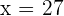 
Wir berechnen die 2. Ableitung
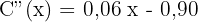
Wir berechnen das Vorzeichen der Nullstellen der 1. Ableitung
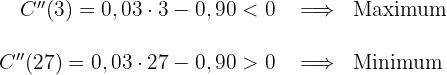
2 Bestimme die Zeiträume, in denen die Aktien gestiegen oder gefallen sind.
Wir bilden Intervalle mit den Nullstellen der 1. Ableitung
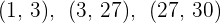
Wir nehmen einen Wert aus jedem Intervall und finden das Vorzeichen, das er in der 1. Ableitung hat:
Ist das Ergebnis positiv, so ist die Funktion auf diesem Intervall steigend.
Ist das Ergebnis negativ, ist die Funktion auf diesem Intervall fallend.
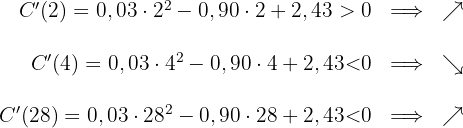
Von 
bis 
und von 
bis steigen die Aktien. Sie fallen von bis .
Angenommen, die Leistung 
eines Schülers in 
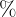in einer 1-stündigen Prüfung ist gegeben durch:
.
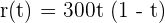Wobei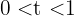 
die Zeit in Stunden ist. Berechne:
1 Wann nimmt die Leistung zu oder ab?
2 Wann ist die Leistung 0?
3 Wann wird die höchste Leistung erzielt und wie lautet diese?
1 Wann nimmt die Leistung zu oder ab?
Wir leiten ab
Wir setzen die Ableitung gleich 0 und ermitteln die Nullstellen der Gleichung
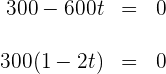
Die Nullstelle ist 
Wir bilden Intervalle mit den Nullstellen der 1. Ableitung
Wir nehmen einen Wert aus jedem Intervall und ermitteln das Vorzeichen, das er in der 1. Ableitung hat:
Ist das Ergebnis positiv, so ist die Funktion auf diesem Intervall steigend.
Ist das Ergebnis negativ, ist die Funktion auf diesem Intervall fallend.
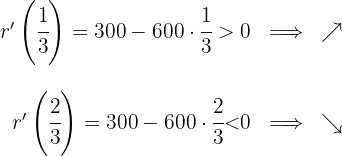
Somit steigt die Funktion bei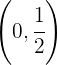 
und fällt bei 
.
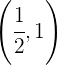2 Wann ist die Leistung 0?
Die Leistung ist 0, wenn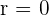 
.
.
Die Nullstellen si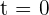nd 
und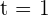 
.
Somit ist die Leistung am Anfang und am Ende der Prüfung 0.
3 Wann wird die höchste Leistung erzielt und wie lautet diese?
Wir berechnen die 2. Ableitung
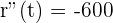
Die 2. Ableitung ist immer negativ, weshalb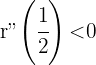 
und es ein Maximum gibt
Wir berechnen die 2. Koordinate des Maximums
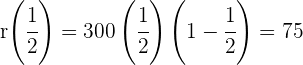
Die höchste Leistung wird also in der Mitte der Prüfung erzielt und beträgt 
.
Berechne die Gleichung der Tangente an den Graphen von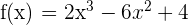 
an seinem Wendepunkt.
1 Wir berechnen die Ableitung
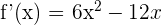
2 Wir berechnen die 2. Ableitung
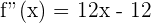
3 Wir setzen die 2. Ableitung gleich 0, um den Wendepunkt zu erhalten.
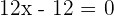
daraus erhalten wir 
Wir berechnen die 3. Ableitung werten für aus
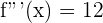
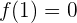
Somit hat die Funktion einen Wendepunkt bei 
.
4 Wir berechnen die Tangente am Wendepunkt, für die wir die Steigung benötigen
Wir wenden die Punkt-Steigungsform an und erhalten
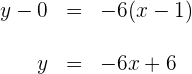
Die Tangente, die durch den Wendepunkt verläuft lautet 
Bestimme 
und 
so, dass die Funktion 
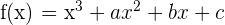für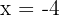 
ein Maximum und für 
ein Minimum hat sowie den Wert für annimmt.
1 Wir berechnen die Ableitung
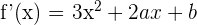
2 Da die Funktion ein Maximum bei 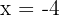und ein Minimum bei hat, ist die Ableitung an diesen Punkten 0. Wir setzen ein und erhalten zwei Gleichungen
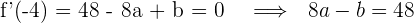
Wir setzen den Wert von 
in die 1. Gleichung ein und erhalten 
3 Da die Funktion den Wert für annimmt
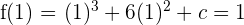
Daraus erhalten wir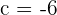 
. Somit lautet die Funktion
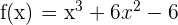
4 Wir berechnen die 2. Ableitung und werten die kritischen Punkte aus
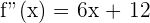
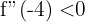, somit hat sie ein Maximum
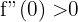ist somit ein Minimum
Bestimme den Wert für 
und 
so, dass die Funktion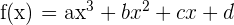 
ein Maximum bei 
und ein Minimum bei 
hat.
1 Wir berechnen die Ableitung
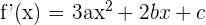
2 Da die Funktion bei ein Maximum und bei 
ein Minimum hat, ist die Ableitung an diesen Punkten 0. Wir setzen ein und erhalten zwei Gleichungen
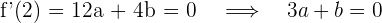
3 Da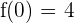 
und 
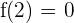, erhalten wir die Gleichungen
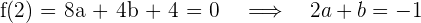
4 Wir lösen das System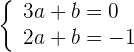 
Wir erhalten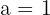 
und 
.
Somit lautet die Funktion
5 Wir berechnen die 2. Ableitung und werten die kritischen Punkte aus
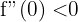, sie hat somit ein Maximum
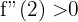, sie hat somit ein Minimum
Bestimme den Wert von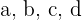 
und 
so, dass der Graph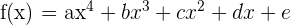 
einen kritischen Punkt bei 
sowie einen Wendepunkt mit der Tangente der Gleichung 
bei 
hat.
1 Wir berechnen die Ableitung
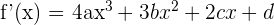
2 Da die Funktion einen kritischen Punkt bei hat, ist die Ableitung an diesem Punkt 0. Wir setzen ein und erhalten die Gleichung
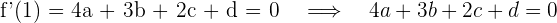
3 Da 
und 
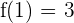, erhalten wir die Gleichungen
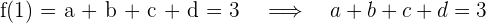
4 Wir berechnen die 2. Ableitung und werten für den Wenkepunkt aus
5 Die Ableitung bei 0 fällt mit der Steigung der Tangente bei 
zusammen.
6 Wir lösen das System 
Wir erhalten 
und 
. Schließlich lautet die Funktion
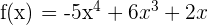
Der Graph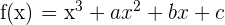 
schneidet die x-Achse bei und hat einen Wendepunkt bei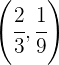 
. Berechne und .
1 Wir berechnen die 2. Ableitung und werten den Wendepunkt aus
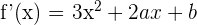
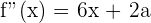
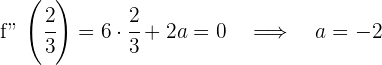
2 Wir werten die Funktion am Wendepunkt aus und erhalten
3 Da 
, erhalten wir die Gleichung
4 Wir lösen das System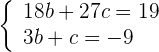 
Wir erhalten 
und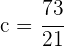 
. Schließlich lautet die Funktion
Gegeben ist die Funktion:
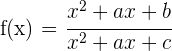
Berechne und so, dass 
bei 
ein lokales Extremum hat und der Graph durch den Koordinatenursprung verläuft.
1 Wir berechnen die Ableitung
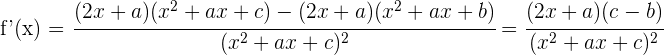
2 Die Ableitung ist 0 bei
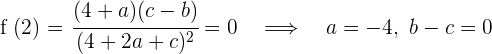
Allerdings kann nicht erfüllt werden, dass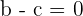 
, da die Funktion 
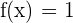wäre und somit nicht durch den Ursprung verlaufen würde
3 Da und 
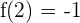, erhalten wir die Gleichungen
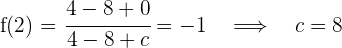
Schließlich lautet die Funktion
Berechne 
und 
, so dass die Funktion: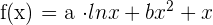 
Extrema an den Punkten und hat. Für diese Werte von und , welche Art von Extrema hat die Funktion bei und 
?
1 Wir berechnen die Ableitung und werten für und aus. An diesen Punkten ist die Ableitung 0, da es sich um Extrema handelt
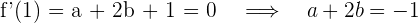
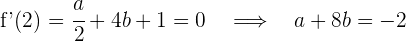
4 Wir lösen das System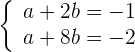 
Wir erhalten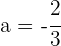 
und 
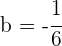. Schließlich lautet die Funktion
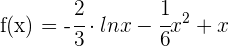
5 Wir berechnen die 2. Ableitung und werten für und aus
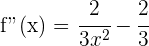
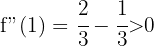, es gibt also ein Minimum bei
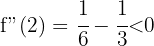, es gibt also ein Maximum bei
Bestimme die Gleichungen der Tangente und der Normalen an ihrem Wendepunkt zum Graphen: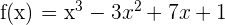 
.
1 Wir berechnen die Ableitung
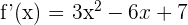
2 Wir berechnen die 2. Ableitung
3 Wir setzen die 2. Ableitung gleich 0, um den Wendepunkt zu erhalten
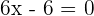
Daraus erhalten wir
Wir berechnen die 3. Ableitung und werten für aus
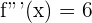
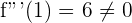
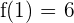
Die Funktion hat also einen Wendepunkt bei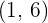 
.
4 Wir berechnen die Tangente am Wendepunkt, für die wir die Steigung benötigen
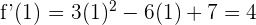
Wir wenden die Punkt-Steigungsform an und erhalten
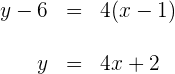
Die Tangente durch den Wendepunkt ist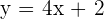 
Wir wenden die Punkt-Steigungsform für die Steigung 
der Normalen an und erhalten
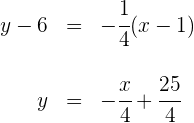
Die Normale durch den Wendepunkt ist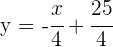 
Der Betrag , der sich im Laufe eines Tages in einem Spielautomaten angesammelt hat, ist ein Satz der Form:
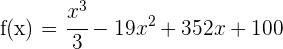
wobei die Variable 
die Zeit in Stunden (von 0 bis 24) angibt. Beantworte folgende Fragen:
1 Geht dem Automaten jemals das Geld aus?
2 Wenn die „Kasse“ nach 24 Stunden erfolgt, führt dies zu einem Gewinn für die Automatenbesitzer?
3 Zu welchem Zeitpunkt ist die Einnahme am höchsten und zu welchem Zeitpunkt am niedrigsten?
4 Wann wird der höchste Preis ausbezahlt?
1 Zwischen 0 und 24 ist die Funktion ungleich 0, so dass der Automat immer Münzen hat.
Es gibt ein absolutes Minimum bei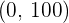 
.
2 Wenn die „Kasse“ nach 24 Stunden erfolgt, führt dies zu einem Gewinn für die Automatenbesitzer?
Gewinn: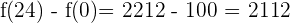 
3 Zu welchem Zeitpunkt ist die Einnahme am höchsten und zu welchem Zeitpunkt am niedrigsten?
Wir berechnen die Ableitung
Wir setzen die Ableitung gleich 0
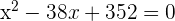
wir erhalten 
und 
4 Wir berechnen die 2. Ableitung und werten für und aus
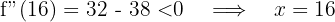ist ein Maximum
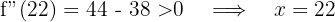ist ein Minimum
So ist der gesammelte Betrag um 16:00 Uhr am höchsten und um 22:00 Uhr am niedrigsten
5 Wann wird der höchste Preis ausbezahlt?
Der höchste Preis entspricht dem Wendepunkt.
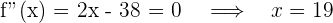
Der höchste Betrag wird also um 19:00 Uhr ausbezahlt
Gegeben ist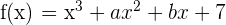 
. Bestimme und so, dass der Graph der Funktion für einen Wendepunkt hat und die Tangente an diesem Punkt einen Winkel von 
mit der x-Achse bildet.
1 Wir berechnen die 1. und 2. Ableitung
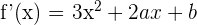
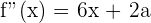
2 Da die Funktion einen Wendepunkt bei hat, ist die Ableitung an diesem Punkt 0. Durch Einsetzen erhalten wir
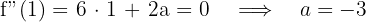
3 Da die Tangente bei einen Winkel von bildet und ihre Steigung gleich dem Tangens dieses Winkels ist, gilt
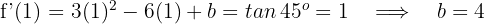
Die Funktion lautet
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
