Maximale Fläche eines in einen Kreis eingeschriebenen Rechtecks
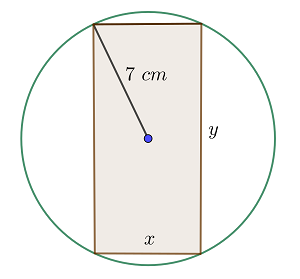
Ermittle die Seiten des Rechtecks mit maximaler Fläche, das in einen Kreis mit dem Radius  eingeschrieben ist.
eingeschrieben ist.
1  sind die Grundseite und die Höhe des Rechtecks.
sind die Grundseite und die Höhe des Rechtecks.
2 Zu optimierende Funktion
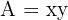
3Wir setzen die Variablen in Relation. Hierfür nehmen wir die Diagonale des Dreiecks und wenden den Satz des Pythagoras an
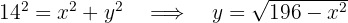
4 Wir setzen in die zu optimierende Funktion ein
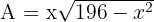
5 Wir leiten die zu optimierende Funktion ab
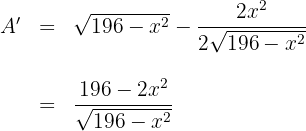
6 Wir setzen die Ableitung gleich 0 und berechnen die Nullstellen
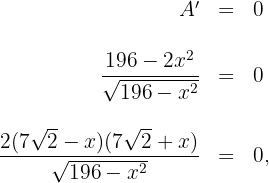
Also ist 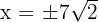 , aber wir nehmen nur das positive Ergebnis
, aber wir nehmen nur das positive Ergebnis
Wir berechnen die Höhe
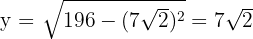
7 Wir berechnen die 2. Ableitung um das erhaltene Ergebnis zu überprüfen
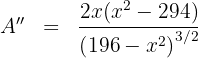
Wir substituieren 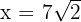
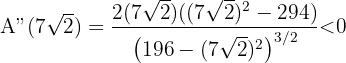
Somit maximiert 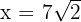 die Fläche. Das Rechteck mit der größten Fläche ist also dasjenige, dessen Grundseite und Höhe gleich
die Fläche. Das Rechteck mit der größten Fläche ist also dasjenige, dessen Grundseite und Höhe gleich 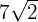 ist.
ist.
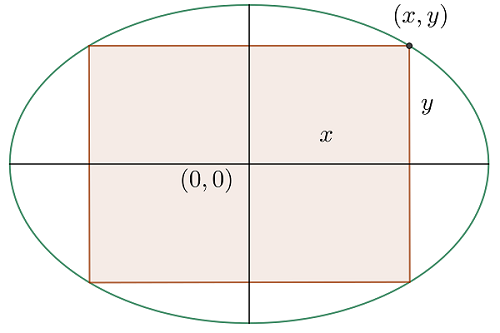
Maximale Fläche eines Rechtecks, das in eine Ellipse eingeschrieben ist
Finde die Seiten des Rechtecks mit maximaler Fläche, das in die Ellipse 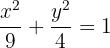 eingeschrieben ist
eingeschrieben ist
1 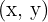 ist ein Eckpunkt des Rechtecks in der Ellipse. Da die Ellipse symmetrisch zum Ursprung ist, ist die Grundseite des Rechtecks
ist ein Eckpunkt des Rechtecks in der Ellipse. Da die Ellipse symmetrisch zum Ursprung ist, ist die Grundseite des Rechtecks  und seine Höhe
und seine Höhe 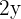
2 Zu optimierende Funktion
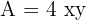
3Wir setzen die Variablen in Relation. Hierfür ermitteln wir eine der Variablen der Ellipsengleichung

4 Wir setzen in die zu optimierende Funktion ein
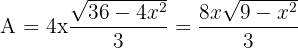
5 Wir leiten die zu optimierende Funktion ab
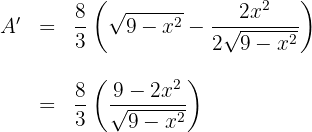
6 Wir setzen die Ableitung gleich 0 und berechnen die Nullstellen
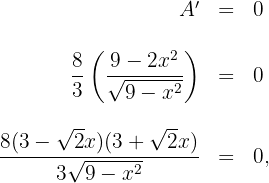
Somit ist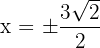 , allerdings nehmen wir nur das positive Ergebnis. Die Grundseite ist
, allerdings nehmen wir nur das positive Ergebnis. Die Grundseite ist 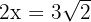
Wir berechnen die Höhe
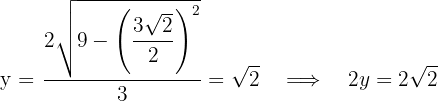
7 Wir berechnen die 2. Ableitung, um das Ergebnis zu überprüfen
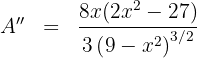
Wir substituieren 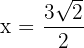
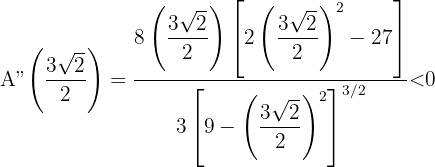
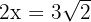 maximiert die Fläche. Das Rechteck mit der größten Fläche ist also dasjenige, dessen Grundfläche und Höhe gleich
maximiert die Fläche. Das Rechteck mit der größten Fläche ist also dasjenige, dessen Grundfläche und Höhe gleich 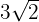 und
und 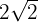 sind
sind
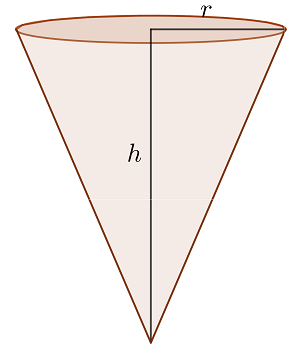
Minimale Seitenfläche eines Kegels
Es ist vorgesehen, einen Kegel (ohne Abdeckung) mit dem Volumen 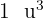 herzustellen. Welche Abmessungen sollte er haben, damit möglichst wenig Material verbraucht wird?
herzustellen. Welche Abmessungen sollte er haben, damit möglichst wenig Material verbraucht wird?
1  ist der Radius der Grundseite des Kegels und
ist der Radius der Grundseite des Kegels und  seine Höhe
seine Höhe
2 Zu optimierende Funktion
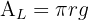
3Wir setzen die Variablen in Relation. Hierfür nehmen wir das Volumen und die Mantellinie
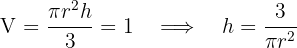
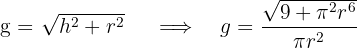
4 Wir setzen in die zu optimierende Funktion ein
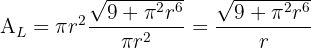
5 Wir leiten die zu optimierende Funktion ab
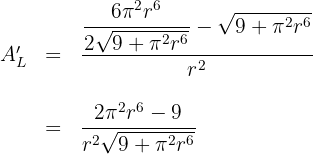
6 Wir setzen die Ableitung gleich 0 und berechnen die Nullstellen
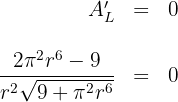
somit ist 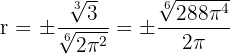 , allerdings nehmen wir nur das positive Ergebnis.
, allerdings nehmen wir nur das positive Ergebnis.
Wir berechnen die Höhe
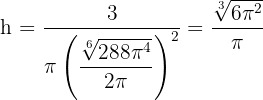
7 Wir berechnen die 2. Ableitung, um das erhaltene Ergebnis zu überprüfen
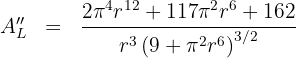
Wir substituieren 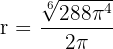
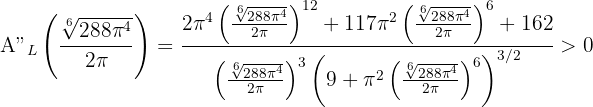
Somit minimiert 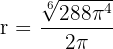 die Seitenfläche. Die Abmessungen des Kegels, die die Seitenfläche minimieren, sind also diejenigen, deren Radius und Höhe
die Seitenfläche. Die Abmessungen des Kegels, die die Seitenfläche minimieren, sind also diejenigen, deren Radius und Höhe 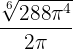 und
und 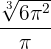 n sind
n sind
Maximales Produkt zweier Zahlen
Finde zwei positive Zahlen, deren Summe gleich  ist und bei denen das Produkt der einen mit dem Quadrat der anderen maximal ist.
ist und bei denen das Produkt der einen mit dem Quadrat der anderen maximal ist.
1 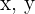 sind zwei positive Zahlen, deren Summe
sind zwei positive Zahlen, deren Summe  ist.
ist.
2 Zu optimierende Funktion:
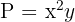
3Wir setzen die Variablen in Relation. Hierfür nehmen wir die Summe der beiden Zahlen

4Wir setzen in die zu optimierende Funktion ein
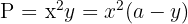
5Wir leiten die zu optimierende Funktion ab
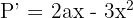
6 Wir setzen die Ableitung gleich 0 und berechnen die Nullstellen
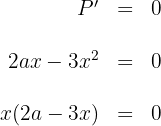
Somit ist 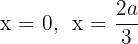 , allerdings nehmen wir nur das positive Ergebnis
, allerdings nehmen wir nur das positive Ergebnis
Wir berechnen den Wert der anderen Zahl
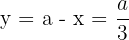
7 Wir berechnen die 2. Ableitung, um das erhaltene Ergebnis zu überprüfen
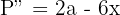
Wir substituieren 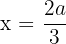
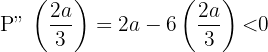
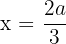 maximiert also das Produkt. Die Zahlen, die das Produkt maximieren, sind also
maximiert also das Produkt. Die Zahlen, die das Produkt maximieren, sind also 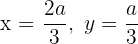
Minimale Fläche zweier Figuren
Man hat einen 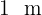 langen Draht und möchte ihn in zwei Teile teilen, um mit einem einen Kreis und mit dem anderen ein gleichseitiges Dreieck zu bilden. Ermittle die Länge der einzelnen Teile, so dass die Summe der Flächen des Kreises und des Dreiecks minimal ist.
langen Draht und möchte ihn in zwei Teile teilen, um mit einem einen Kreis und mit dem anderen ein gleichseitiges Dreieck zu bilden. Ermittle die Länge der einzelnen Teile, so dass die Summe der Flächen des Kreises und des Dreiecks minimal ist.
1  ist der Radius des Kreises und
ist der Radius des Kreises und 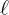 die Seite des gleichseitigen Dreiecks.
die Seite des gleichseitigen Dreiecks.
2 Zu optimierende Funktion:
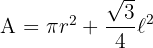
3Wir setzen die Variablen in Relation. Hierfür nehmen wir die Summe der beiden Umfänge
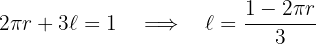
4Wir setzen in die zu optimierende Funktion ein
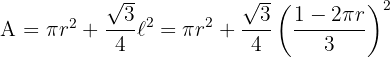
5Wir leiten die zu optimierende Funktion ab
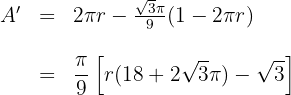
6 Wir setzen die Ableitung gleich 0 und berechnen die Nullstellen
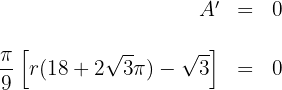
Somit ist 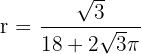
Wir ermitteln den Wert der Seite des Dreiecks
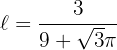
7 Wir berechnen die 2. Ableitung, um das erhaltene Ergebnis zu überprüfen
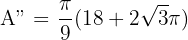
Wir substituieren 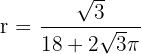
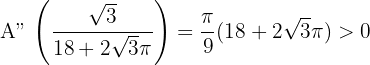
Somit minimiert 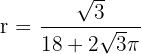 die Fläche. Der Draht wird also in Stücke von
die Fläche. Der Draht wird also in Stücke von 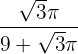 für den Kreis und
für den Kreis und 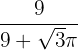 für das gleichseitige Dreieck geteilt.
für das gleichseitige Dreieck geteilt.
Maximale Fläche eines in ein spitzwinkliges Dreieck eingeschriebenen Rechtecks
Ermittle die Abmessungen des größten in ein spitzwinkliges Dreieck eingeschriebenen Rechtecks, wenn eine der Seiten des Rechtecks in der Grundseite des Dreiecks enthalten ist.
1 Wir haben den spitzen Winkel  zur Basis
zur Basis  und die Höhe
und die Höhe  . Außerdem das Dreieck mit den Seiten
. Außerdem das Dreieck mit den Seiten  , wobei die Seite
, wobei die Seite  in der Grundseite des Dreiecks enthalten ist, und die gegenüberliegende Seite mit den Enden
in der Grundseite des Dreiecks enthalten ist, und die gegenüberliegende Seite mit den Enden  auf den beiden anderen Seiten des Dreiecks.
auf den beiden anderen Seiten des Dreiecks.
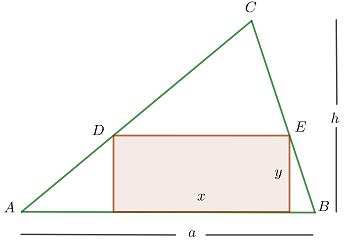
2 Zu optimierende Funktion
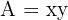
3Wir setzen die Variablen in Relation. Hierfür nehmen wir die ähnlichen Dreiecke  und
und 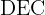

4 Wir setzen in die zu optimierende Funktion ein
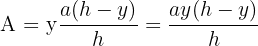
5 Wir leiten die zu optimierende Funktion ab
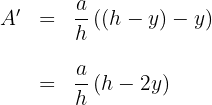
6 Wir setzen die Ableitung gleich 0 und berechnen die Nullstellen
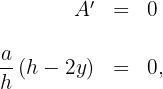
Somit ist 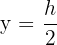
Wir berechnen die Grundseite
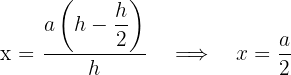
7 Wir berechnen die 2. Ableitung, um das erhaltene Ergebnis zu überprüfen
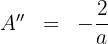
Wir substituieren 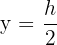
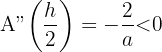
Somit maximiert 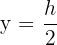 die Fläche des Rechtecks. Das gesuchte Rechteck mit der größten Fläche ist also dasjenige, dessen Grundfläche und Höhe
die Fläche des Rechtecks. Das gesuchte Rechteck mit der größten Fläche ist also dasjenige, dessen Grundfläche und Höhe  und
und  sind.
sind.
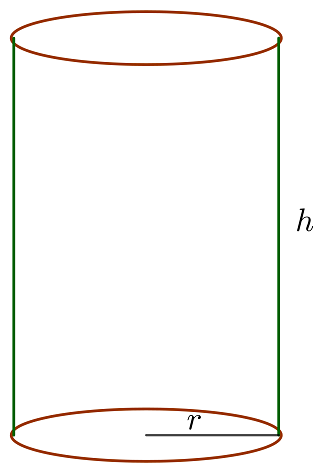
Minimale Kosten für einen zylindrischen Behälter
Ermittle die Abmessungen, die die Kosten eines zylindrischen Behälters auf ein Minimum reduzieren, wenn man weiß, dass sein Volumen 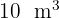 betragen muss und die Herstellungskosten pro
betragen muss und die Herstellungskosten pro 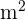
 € für den Boden betragen; außerdem
€ für den Boden betragen; außerdem 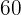 für den Deckel und
für den Deckel und  für jede Seitenfläche.
für jede Seitenfläche.
1 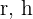 sind der Radius und die Höhe des Zylinders
sind der Radius und die Höhe des Zylinders
2 Zu optimierende Funktion
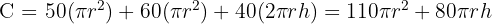
3Wir setzen die Variablen in Relation. Hierfür nehmen wir das Volumen 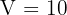 des Behälters
des Behälters
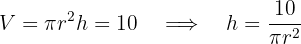
4 Wir setzen in die zu optimierende Funktion ein
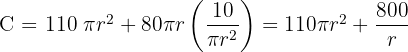
5 Wir leiten die zu optimierende Funktion ab
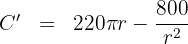
6 Wir setzen die Ableitung gleich 0 und berechnen die Nullstellen
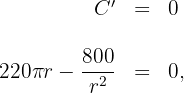
Somit ist 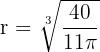
Wir berechnen die Höhe
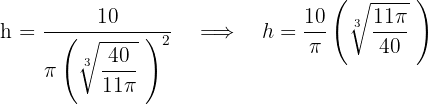
7 Wir berechnen die 2. Ableitung, um das erhaltene Ergebnis zu überprüfen
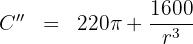
Wir substituieren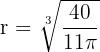
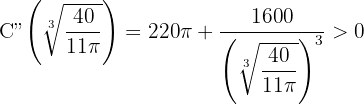
Somit minimieren 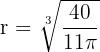 und
und 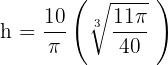 die Kosten des Behälters.
die Kosten des Behälters.
Minimaler Umfang
Ein Landwirt möchte ein rechteckiges Grundstück von 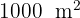 eingrenzen. Das Grundstück soll eingezäunt und durch einen parallelen Zaun an zwei Seiten in zwei gleiche Teile geteilt werden. Wie groß ist das Grundstück, für das ein Mindestmaß an Zaun benötigt wird?
eingrenzen. Das Grundstück soll eingezäunt und durch einen parallelen Zaun an zwei Seiten in zwei gleiche Teile geteilt werden. Wie groß ist das Grundstück, für das ein Mindestmaß an Zaun benötigt wird?
1 Das Grundstück hat die Grundseite  und die Höhe
und die Höhe 

2 Zu optimierende Funktion
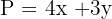
3Wir setzen die Variablen in Relation. Hierfür nehmen wir die Fläche des Grundstücks 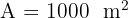
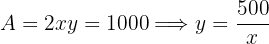
4 Wir setzen in die zu optimierende Funktion ein
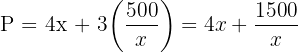
5 Wir leiten die zu optimierende Funktion ab
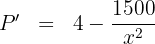
6 Wir setzen die Ableitung gleich 0 und berechnen die Nullstellen
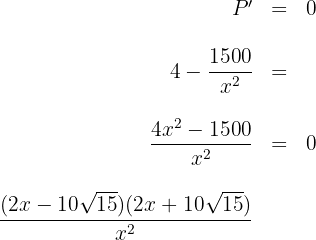
Wir erhalten 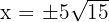 und wählen das positive Ergebnis.
und wählen das positive Ergebnis.
Wir ermitteln die Höhe
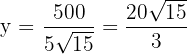
7 Wir berechnen die 2. Ableitung, um das erhaltene Ergebnis zu überprüfen
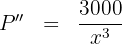
Wir substituieren 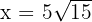
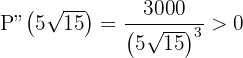
Somit minimieren 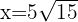 und
und 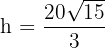 die Kosten für den Zaun.
die Kosten für den Zaun.
Minimale Zeit
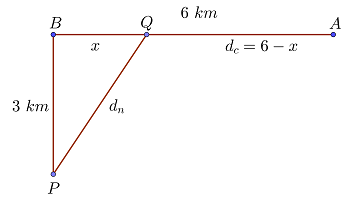
Eine Person auf einer Insel möchte einen Punkt  an einem geradlinigen Strand auf dem Festland erreichen. Die Person ist
an einem geradlinigen Strand auf dem Festland erreichen. Die Person ist 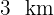 vom nächsten Punkt
vom nächsten Punkt  am Strand entfernt und der Punkt
am Strand entfernt und der Punkt  ist
ist 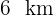 von
von  entfernt. Wenn die Person mit
entfernt. Wenn die Person mit 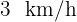 schwimmt und mit
schwimmt und mit 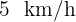 geht, ermittle, an welchen Punkt am Strand sie ankommen sollte (nach dem sie geschwommen ist) um ihre Zeit zu minimieren.
geht, ermittle, an welchen Punkt am Strand sie ankommen sollte (nach dem sie geschwommen ist) um ihre Zeit zu minimieren.
1  ist die Distanz von
ist die Distanz von  zum Punkt am Strand, an dem die Person ankommt,
zum Punkt am Strand, an dem die Person ankommt, 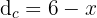 ist die zu Fuß zurückgelegte Distanz
ist die zu Fuß zurückgelegte Distanz
2 Zu optimierende Funktion
Zunächst berechnen wir die durch Schwimmen zurückgelegte Distanz mit dem Satz des Pythagoras
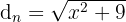
Die Zeiten sind
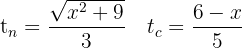
Die zu optimierende Funktion ist gleich der Summe der Zeiten
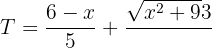
3 Wir leiten die zu optimierende Funktion ab
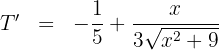
4 Wir setzen die Ableitung gleich 0 und berechnen die Nullstellen
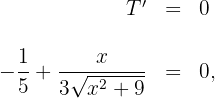
Somit ist 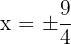 und wir nehmen das positive Ergebnis.
und wir nehmen das positive Ergebnis.
5 Wir berechnen die 2. Ableitung, um das erhaltene Ergebnis zu überprüfen
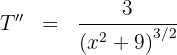
Wir substituieren 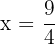
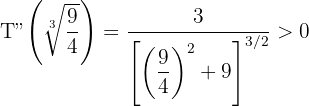
Die minimale Zeit liegt vor, wenn 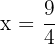 . Die Person muss also
. Die Person muss also 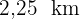 vom Punkt
vom Punkt  aus schwimmen und
aus schwimmen und 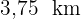 bis zum Ziel gehen.
bis zum Ziel gehen.
Maximale Fläche eines gleichschenkligen Dreiecks
Wie lang müssen die Seiten eines gleichschenkligen Dreiecks mit dem Umfang  sein, damit die Fläche maximal ist?
sein, damit die Fläche maximal ist?
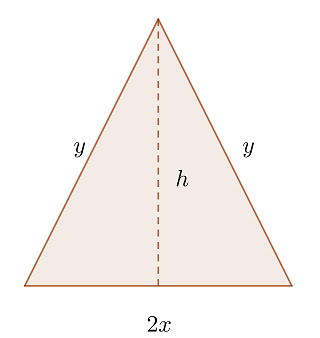
1  sind die gleich langen Seiten des gleichschenkligen Dreiecks,
sind die gleich langen Seiten des gleichschenkligen Dreiecks,  ist die Grundseite und
ist die Grundseite und  die Höhe
die Höhe
2 Zu optimierende Funktion
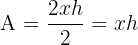
3Wir setzen die Variablen in Relation. Hierfür nehmen wir den Umfang und die Höhe
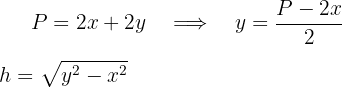
Wir setzen den Ausdruck von  in die Höhe ein
in die Höhe ein
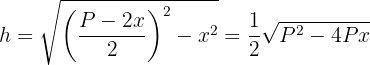
4 Wir setzen den Ausdruck der Höhe in die zu optimierende Funktion ein
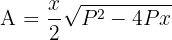
5 Wir leiten die zu optimierende Funktion ab
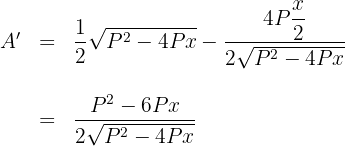
6 Wir setzen die Ableitung gleich 0 und berechnen die Nullstellen
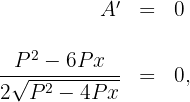
Somit ist 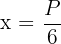 . Wir stellen fest, dass die Ableitung bei
. Wir stellen fest, dass die Ableitung bei 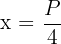 nicht definiert ist
nicht definiert ist
Wir berechnen den Wert der Seite 
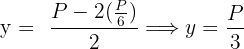
7 Wir berechnen die 2. Ableitung, um das erhaltene Ergebnis zu überprüfen
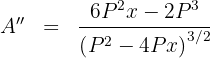
Wir substituieren 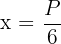
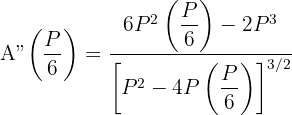 und das Dreieck ist gleichseitig.
und das Dreieck ist gleichseitig.
Mit KI zusammenfassen:


