Beispiele für Optimierungsprobleme und deren Lösung.
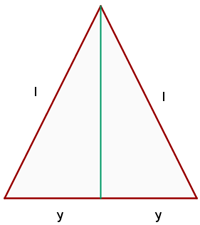
Finde von allen gleichschenkligen Dreiecken mit 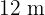 Umfang die Seiten des Dreiecks mit dem größten Flächeninhalt.
Umfang die Seiten des Dreiecks mit dem größten Flächeninhalt. 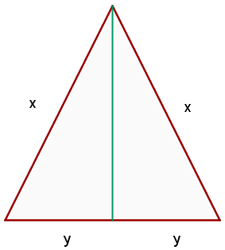
Wir müssen den Flächeninhalt des Dreiecks optimieren (maximieren), d. h. die durch den Flächeninhalt definierte Funktion. Da das Dreieck gleichschenklig ist, ist seine Grundseite die Seite 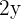 , die gleichen Seiten sind
, die gleichen Seiten sind  , und seine Höhe können wir mithilfe des Satzes des Pythagoras berechnen,
, und seine Höhe können wir mithilfe des Satzes des Pythagoras berechnen, 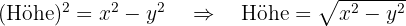 wir erhalten also
wir erhalten also
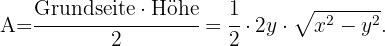
Unter der Voraussetzung, dass der Umfang des Dreiecks 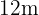 beträgt, können wir die Variablen in Beziehung setzen:
beträgt, können wir die Variablen in Beziehung setzen:
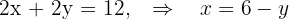
Dieses Ergebnis können wir in die Funktion einsetzen:
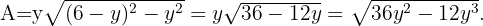
Um die lokalen Extrema zu finden, leiten wir ab, setzen sie gleich 0 und berechnen die Nullstellen:
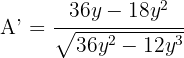
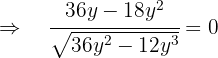
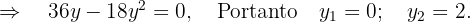
Wir denken daran, dass wir ein lokales Maximum erhalten, wenn die 2. Ableitung ein negatives Vorzeichen hat. Wir führen also die 2. Ableitung durch und werten nach  aus, da die Lösung
aus, da die Lösung  nicht möglich ist.
nicht möglich ist.
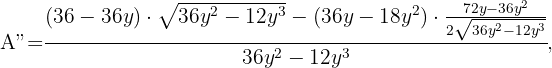
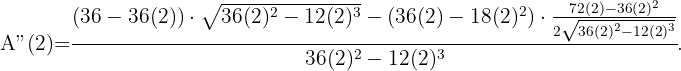
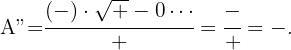
Es ist also bewiesen, dass es bei  ein Maximum gibt. Die Grundseite
ein Maximum gibt. Die Grundseite 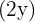 misst
misst 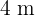 und die schiefen Seiten
und die schiefen Seiten 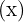 messen ebenfalls
messen ebenfalls 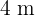 , so dass das Dreieck mit dem größten Flächeninhalt ein gleichseitiges Dreieck wäre.
, so dass das Dreieck mit dem größten Flächeninhalt ein gleichseitiges Dreieck wäre.
Der Wert eines Diamanten ist proportional zum Quadrat seines Gewichts. Teilen Sie einen 2 g schweren Diamanten in zwei Teile, sodass die Summe der Werte der beiden entstandenen Diamanten minimal ist.
Angenommen,  ist das Gewicht eines Diamanten. Da der Wert des Diamanten proportional zum Quadrat des Gewichts ist, muss der Wert unseres Diamanten durch
ist das Gewicht eines Diamanten. Da der Wert des Diamanten proportional zum Quadrat des Gewichts ist, muss der Wert unseres Diamanten durch  gegeben sein, wobei
gegeben sein, wobei  eine positive Proportionalitätskonstante ist. Wenn man einen Diamanten von
eine positive Proportionalitätskonstante ist. Wenn man einen Diamanten von 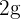 in zwei Teile mit den Gewichten
in zwei Teile mit den Gewichten  und
und  teilt, erhält man eine Gleichung, die die Werte von
teilt, erhält man eine Gleichung, die die Werte von  und
und  miteinander in Beziehung setzt,
miteinander in Beziehung setzt,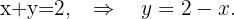
Die Werte der einzelnen Teile sind also: 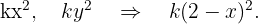
Und die Funktion, die wir optimieren wollen, ist diejenige, die sich aus der Summe dieser Werte ergibt: 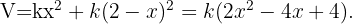
Um die Extremwerte dieser Funktion zu finden, müssen wir ableiten und gleich 0 setzen:
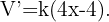

Wie wir sehen können, haben wir eine Lösung  für unser Problem. Um zu prüfen, ob diese Lösung einen Minimalwert ergibt, berechnen wir die 2. Ableitung und prüfen, ob sie tatsächlich positiv ist,
für unser Problem. Um zu prüfen, ob diese Lösung einen Minimalwert ergibt, berechnen wir die 2. Ableitung und prüfen, ob sie tatsächlich positiv ist,

Auf diese Weise muss der Diamant in zwei gleiche Teile von je 1 g geteilt werden.
Finde unter allen Geraden, die entlang des Punkts  verlaufen, diejenige, die mit den positiven Teilen der Koordinatenachsen ein Dreieck mit minimalem Flächeninhalt bildet.
verlaufen, diejenige, die mit den positiven Teilen der Koordinatenachsen ein Dreieck mit minimalem Flächeninhalt bildet.
Aus der Punkt-Steigungsform der Geraden erhalten wir, dass die Gleichung der Geraden, die durch den Punkt  verläuft, wie folgt lautet:
verläuft, wie folgt lautet:
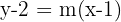
Da die Eckpunkte auf den positiven Teilen der Koordinatenachsen liegen sollen, benötigen wir den Wert, den  annimmt, wenn
annimmt, wenn  und den Wert, den
und den Wert, den  annimmt, wenn
annimmt, wenn  .
.
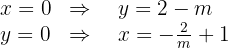
Somit sind 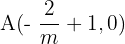 und
und 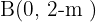 Scheitelpunkte des Dreiecks.
Scheitelpunkte des Dreiecks. 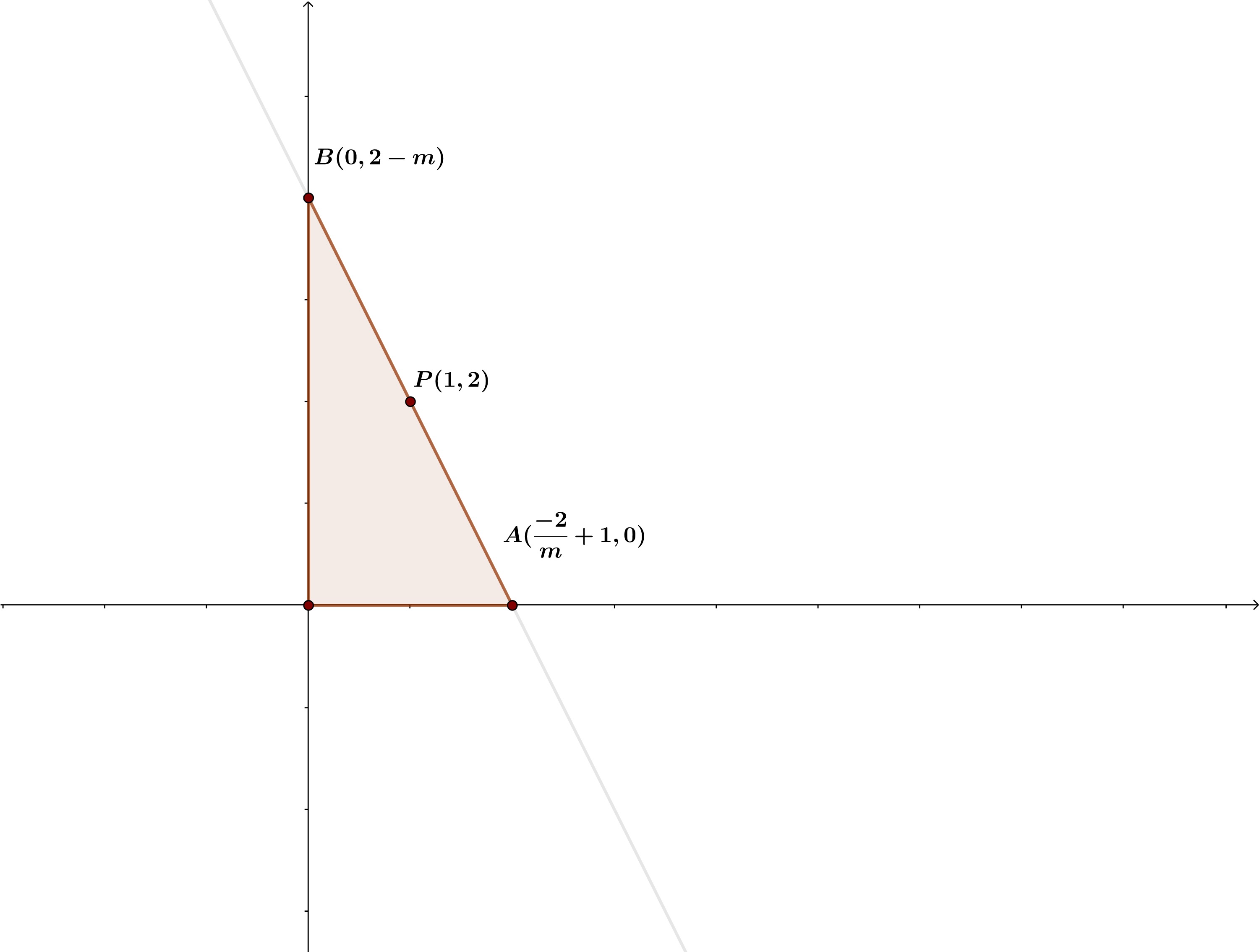
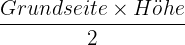
In diesem Fall ist 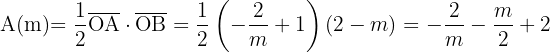
Wir berechnen die Ableitung und setzen sie gleich 0, um die kritischen Werte zu ermitteln: 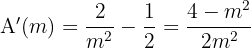
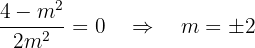
Wir stellen fest, dass mit  kein Dreieck gebildet würde, weil die Koordinaten von A und B mit dem Koordinatenursprung zusammenfallen, also nehmen wir
kein Dreieck gebildet würde, weil die Koordinaten von A und B mit dem Koordinatenursprung zusammenfallen, also nehmen wir 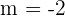
Wir berechnen die 2. Ableitung und setzen ein: 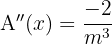
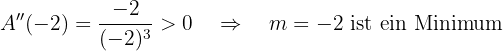
Somit ist die Gerade die Gerade, die die Steigung 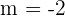 hat
hat
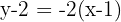
Eine Boje, die aus zwei geraden, an der Basis verbundenen Eisenkegeln besteht, soll mithilfe von zwei kreisförmigen Platten mit einem Radius von  gebaut werden. Berechne die Maße der Boje, sodass ihr Volumen maximal ist.
gebaut werden. Berechne die Maße der Boje, sodass ihr Volumen maximal ist. 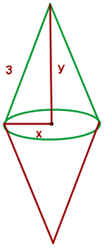
Die Formel für das Volumen eines Kegels ist 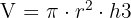
In diesem Fall würde die zu optimierende Funktion laut Abbildung wie folgt lauten: 
Wir setzen die Variablen in Beziehung: 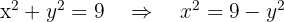
Wir setzen in die Funktion ein: 
Wir leiten ab, setzen gleich 0 und berechnen die Nullstellen.
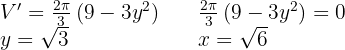
Wir ermitteln die 2. Ableitung, um das Ergebnis zu überprüfen
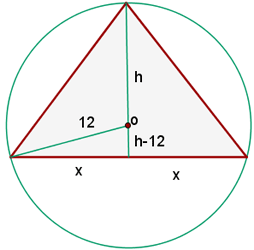
Ermittle das gleichschenklige Dreieck mit der größten Fläche, das in einen Kreis mit dem Radius 12 cm eingeschrieben ist.
Die Fläche der Dreiecke ist durch 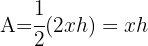 gegeben.
gegeben.
Die Abbildung zeigt ein rechtwinkliges Dreieck, das mit dem Radius des Kreises, einer Seite des Dreiecks und seiner Höhe gebildet wird. Wir wenden den Satz des Pythagoras an und erhalten 
Wir setzen in  ein und erhalten
ein und erhalten 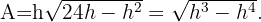
Nun leiten wir ab 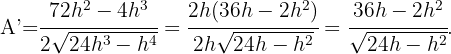 Wir setzen gleich 0 und erhalten
Wir setzen gleich 0 und erhalten 
Mit diesen Werten können wir das Folgende über die Werte des Dreiecks sagen:
Grundseite: ,
,
Seite: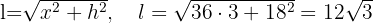
Um zu prüfen, ob diese Werte ein Maximum für die Fläche ergeben, müssen wir die 2. Ableitung für 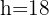 auswerten und erhalten einen negativen Wert:
auswerten und erhalten einen negativen Wert:
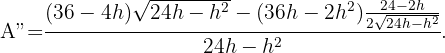
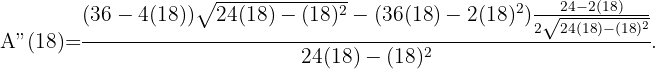
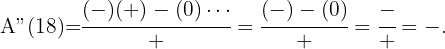
Ein gleichschenkliges Dreieck mit dem Umfang  dreht sich um seine Höhe und bildet einen Kegel. Welchen Wert muss die Grundseite haben, damit das Volumen des Kegels maximal ist?
dreht sich um seine Höhe und bildet einen Kegel. Welchen Wert muss die Grundseite haben, damit das Volumen des Kegels maximal ist?
Die zu optimierende Funktion wird durch das Volumen des Kegels definiert, der durch die Drehung des Dreiecks gebildet wird, 
Da der Umfang  beträgt und das Dreieck sich um seine Höhe dreht, erhalten wir aus der Figur Folgendes:
beträgt und das Dreieck sich um seine Höhe dreht, erhalten wir aus der Figur Folgendes: 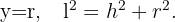
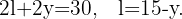
Wenn wir diese Gleichungen kombinieren, erhalten wir 
Da wir nun alle Variablen in Form von  haben, können wir in die Volumenfunktion einsetzen,
haben, können wir in die Volumenfunktion einsetzen,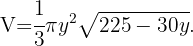
Nun leiten wir ab: 
Wir setzen gleich 0 und erhalten die folgenden Werte für 

und für die Grundseite des Dreiecks; Grundseite: 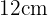 ,
,
Um zu überprüfen, ob wir bei 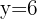 ein Maximum erhalten, müssen wir die 2. Ableitung von
ein Maximum erhalten, müssen wir die 2. Ableitung von  zu diesem Wert berechnen und erhalten einen negativen Wert:
zu diesem Wert berechnen und erhalten einen negativen Wert:
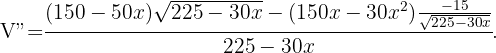
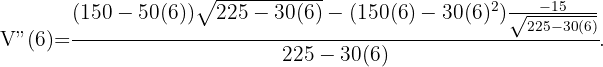

Es soll eine zylindrische Blechdose (mit Deckel) mit einem Fassungsvermögen von 1 Liter hergestellt werden. Welche Abmessungen sollte sie haben, damit möglichst wenig Metall verwendet wird?
Die Aufgabe besteht darin, die Funktion zu minimieren, die die Fläche der zylindrischen Dose definiert. Diese ist gegeben durch 
Da die Dose 1 Liter fassen muss, ist ihr Volumen gleich  , das heißt,
, das heißt, 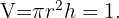
Wir bestimmen  und erhalten
und erhalten 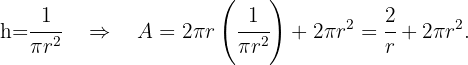
Wir leiten die Funktion ab: 
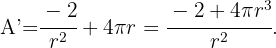
Um die Extremwerte zu finden, setzen wir die obige Gleichung gleich 0 und ermitteln den Wert von 

Wir erhalten den Wert von  mithilfe des Werts von
mithilfe des Werts von  ,
,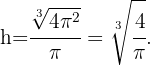
Durch Überprüfung mit der 2. Ableitung ergibt sich, dass 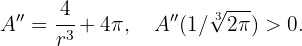
Daher sind die Abmessungen der Dose minimal mit 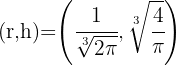 .
.
Zerlege die Zahl 44 in zwei Summanden, sodass das Fünffache des Quadrats der ersten Zahl plus das Sechsfache des Quadrats der zweiten Zahl ein Minimum ergibt.
Wir wollen die Zahl  in zwei Summanden zerlegen, also
in zwei Summanden zerlegen, also 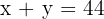 ,
,
und wir möchten, dass das Fünffache des Quadrats des ersten plus das Sechsfache des Quadrats des zweiten ein Minimum ist, sodass 
Da 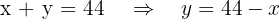 ,
,
setzen wir " "
"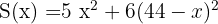 ein
ein
Wir leiten ab und setzen gleich 0: 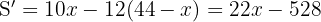

Wir berechnen die 2. Ableitung 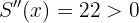
Daher sind das Minimum und die Zahlen 
Man hat einen 1 m langen Draht und möchte ihn in zwei Teile teilen, um mit einem einen Kreis und mit dem anderen ein Quadrat zu bilden. Bestimme die Länge der einzelnen Teile, sodass die Summe der Flächen des Kreises und des Quadrats minimal ist.
Wenn das Quadrat die Seitenlänge  und der Kreis den Radius
und der Kreis den Radius  hat, dann lautet die zu optimierende Funktion:
hat, dann lautet die zu optimierende Funktion: 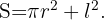
Da der Draht eine Länge von  hat, ergibt die Summe der Umfänge des Kreises und des Quadrats die Gleichung für die Variablen,
hat, ergibt die Summe der Umfänge des Kreises und des Quadrats die Gleichung für die Variablen, 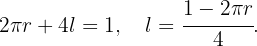
Wir setzen in  ein und erhalten
ein und erhalten 
Nun leiten wir die Funktion  ab und setzen sie gleich 0, um die Extremwerte zu berechnen,
ab und setzen sie gleich 0, um die Extremwerte zu berechnen, 
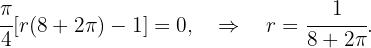
Mit diesem Wert für  gilt: Stück des Kreises:
gilt: Stück des Kreises: 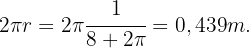 Stück des Quadrats:
Stück des Quadrats:
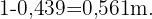
Wie immer bei dieser Art von Problemen besteht der letzte Teil der Minimierung darin, die 2. Ableitung zu finden und zu prüfen, ob sie für die gefundenen Werte positiv ist.
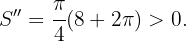
Ermittle die Maße des größten Rechtecks, das in ein gleichschenkliges Dreieck mit der Grundseite  und der Höhe
und der Höhe 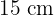 eingeschrieben ist.
eingeschrieben ist.
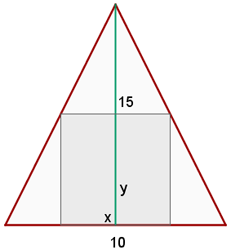
Die zu optimierende Funktion ist Wir setzen die Variablen in Beziehung: Da wir zwei ähnliche Dreiecke haben, erhalten wir
Wir setzen die Variablen in Beziehung: Da wir zwei ähnliche Dreiecke haben, erhalten wir 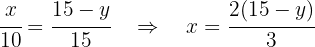
Wir setzen in die Funktion ein: 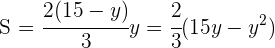
Wir leiten ab, setzen gleich 0 und berechnen die Nullstellen 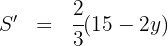 Wir setzen gleich 0 und berechnen die Nullstellen
Wir setzen gleich 0 und berechnen die Nullstellen 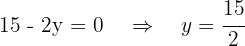
Die Grundseite ist also 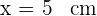 . Wir führen die 2. Ableitung durch, um das Ergebnis zu überprüfen
. Wir führen die 2. Ableitung durch, um das Ergebnis zu überprüfen 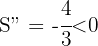
Für 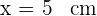 und
und  existiert somit ein relatives Maximum.
existiert somit ein relatives Maximum.
Aus einem Stück Karton mit den Maßen 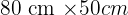 schneidet man aus jeder Ecke ein Quadrat mit der Seite
schneidet man aus jeder Ecke ein Quadrat mit der Seite  aus und faltet es (siehe Abbildung), sodass eine Schachtel entsteht. Berechne
aus und faltet es (siehe Abbildung), sodass eine Schachtel entsteht. Berechne  so, dass das Volumen dieser Schachtel maximal ist.
so, dass das Volumen dieser Schachtel maximal ist.
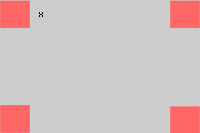
Zunächst müssen wir die zu optimierende Funktion finden. Diese Funktion wird durch das Volumen der Schachtel definiert, die als Seiten  ,
,  und als Höhe
und als Höhe  hat, so dass unsere Funktion wie folgt lautet:
hat, so dass unsere Funktion wie folgt lautet: 
Beachte, dass bei diesem Problem nur eine Variable betroffen ist, so dass wir direkt zur Ermittlung der lokalen Extrema übergehen können. Wir denken daran, dass wir dazu unsere Funktion ableiten und die resultierende Gleichung gleich 0 setzen müssen. 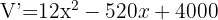
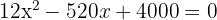
Diese Gleichung lässt sich mit der allgemeinen Formel lösen: 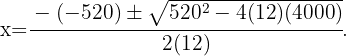
Daraus erhalten wir die beiden folgenden Lösungen: 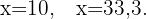
Wir stellen fest, dass die Lösung 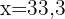 nicht gültig ist, da die Seite
nicht gültig ist, da die Seite  negativ wäre. Unser einziges lokales Extremum ist also
negativ wäre. Unser einziges lokales Extremum ist also 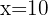 . Wir berechnen die 2. Ableitung der Funktion
. Wir berechnen die 2. Ableitung der Funktion 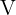 und werten für
und werten für 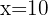 aus. Wir erhalten
aus. Wir erhalten 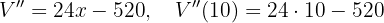 haben.
haben.
Ein Blatt Papier muss 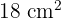 bedruckten Text, einen oberen und unteren Rand von
bedruckten Text, einen oberen und unteren Rand von 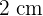 Höhe und seitliche Ränder von
Höhe und seitliche Ränder von 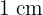 Breite aufweisen. Ermittle die Maße, die die Papierfläche minimieren.
Breite aufweisen. Ermittle die Maße, die die Papierfläche minimieren.

Die zu minimierende Funktion ist durch die Fläche der Papieroberfläche gegeben, nämlich 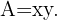
Aus den Bedingungen des Problems müssen wir Gleichungen ableiten, die die Variablen in Beziehung setzen. Da wir 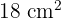 an gedrucktem Text haben müssen, können wir sagen, dass
an gedrucktem Text haben müssen, können wir sagen, dass 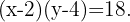
Wenn wir nach  auflösen, erhalten wir
auflösen, erhalten wir 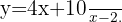 Wir setzen in die Funktion
Wir setzen in die Funktion  ein und erhalten
ein und erhalten 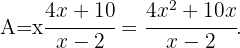
Wir können nun die Funktion ableiten, um die lokalen Extrema zu ermitteln: 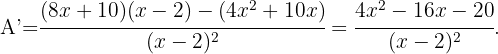
Wir setzen die Ableitung gleich 0: 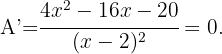
Dies bedeutet, dass wir die Gleichung 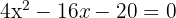 lösen müssen. Wir stellen fest, dass
lösen müssen. Wir stellen fest, dass 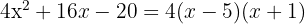
Somit sind unsere Lösungen  und
und  . Die Lösung
. Die Lösung  müssen wir verwerfen, da sie negativ ist. Wir haben also eine einzige Lösung für unser Problem.
müssen wir verwerfen, da sie negativ ist. Wir haben also eine einzige Lösung für unser Problem.
Da wir die 2. Ableitung nicht zu berechnen brauchen, können wir daraus schließen, dass  und
und 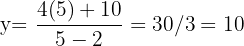 die Papierfläche minimieren.
die Papierfläche minimieren.
Der monatliche Nettogewinn eines Unternehmens, das Busse herstellt, in Millionen Euro, wird durch folgende Funktion angegeben: 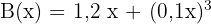 , wobei
, wobei  die Anzahl der produzierten Busse pro Monat ist. Berechne die monatliche Produktion, die den Gewinn maximiert.
die Anzahl der produzierten Busse pro Monat ist. Berechne die monatliche Produktion, die den Gewinn maximiert.
Wir leiten die monatliche Gewinnfunktion ab und setzen sie gleich 0 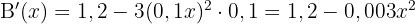
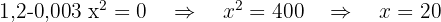
Wir berechnen die 2. Ableitung und setzen ein: 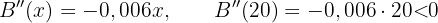
Also maximal.
Eine Obstplantage besteht derzeit aus 25 Bäumen, die jeweils 600 Früchte tragen. Es wird geschätzt, dass für jeden zusätzlich gepflanzten Baum die Produktion jedes Baumes um 15 Früchte abnimmt. Berechne:
1 Aktuellen Ertrag der Plantage.
2 Den Ertrag, der von jedem Baum erzielt werden würde, wenn x weitere Bäume gepflanzt würden.
3 Der Ertrag, den die gesamte Obstanlage liefern würde, wenn x weitere Bäume gepflanzt würden.
4 Wie hoch sollte die Gesamtzahl der Bäume in der Obstplantage sein, um einen maximalen Ertrag zu erzielen?
1 Aktueller Ertrag der Plantage:Aktueller Ertrag: 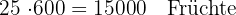
2 Der Ertrag, der sich aus jedem Baum ergibt, wenn  mehr Bäume gepflanzt werden: Wenn
mehr Bäume gepflanzt werden: Wenn  mehr Bäume gepflanzt werden, beträgt der Ertrag jedes Baumes:
mehr Bäume gepflanzt werden, beträgt der Ertrag jedes Baumes: 
3 Der Ertrag der gesamten Obstanlage, wenn  mehr Bäume gepflanzt werden:
mehr Bäume gepflanzt werden: 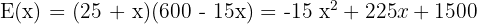
4 Wie hoch sollte die Gesamtzahl der Bäume in der Obstplantage sein, um einen maximalen Ertrag zu erzielen? Wir leiten ab und setzen gleich 0: 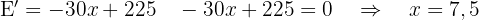 Da die 2. Ableitung negativ ist, gilt:
Da die 2. Ableitung negativ ist, gilt: 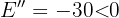 Der maximale Ertrag würde also mit
Der maximale Ertrag würde also mit 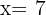 erreicht werden. Der Ertrag wäre maximal, wenn:
erreicht werden. Der Ertrag wäre maximal, wenn:
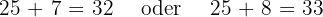
Ein Kreissektor hat einen Umfang von 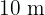 . Berechne den Radius und die Weite des Sektors mit der größten Fläche.
. Berechne den Radius und die Weite des Sektors mit der größten Fläche. 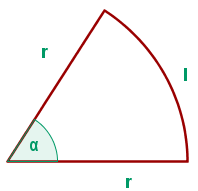
Unsere zu optimierende Funktion ist diejenige, die durch die Fläche des Kreissektors definiert ist, wie in der Abbildung zu sehen: 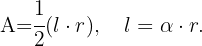
Da der Umfang 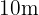 ist, gilt
ist, gilt 
Wenn wir in die Funktion  einsetzen, haben wir
einsetzen, haben wir 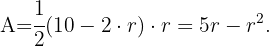
Nun leiten wir die Funktion  ab und setzen sie gleich 0, um einen Extremwert zu erhalten:
ab und setzen sie gleich 0, um einen Extremwert zu erhalten: 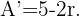
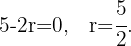
Nachdem wir einen Wert für de obtener un valor para  erhalten haben, können wir Werte für
erhalten haben, können wir Werte für  und
und 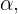 bestimmen:
bestimmen: 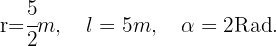
In diesem Fall ist die 2. Ableitung von  konstant und negativ:
konstant und negativ: 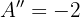 ergeben.
ergeben.
Mit KI zusammenfassen:


