Bestimme die Gleichung einer Hyperbel mit dem Brennpunkt  , dem Scheitelpunkt
, dem Scheitelpunkt  und dem Mittelpunkt
und dem Mittelpunkt  .
.
1 Da der Mittelpunkt und der Scheitelpunkt auf der x-Achse liegen, hat die Gleichung folgende Form

Wir berechnen den Wert für  , der dem Abstand vom Mittelpunkt bis zu einem der Scheitelpunkte entspricht
, der dem Abstand vom Mittelpunkt bis zu einem der Scheitelpunkte entspricht

2 Wir berechnen den Wert für  , der dem Abstand vom Mittelpunkt bis zu einem der Brennpunkte entspricht
, der dem Abstand vom Mittelpunkt bis zu einem der Brennpunkte entspricht

3 Wir berechnen den Wert für 

4 Die Gleichung der Hyperbel lautet

Bestimme die Gleichung und die Exzentrizität der Hyperbel mit den Brennpunkten 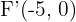 und
und  , und
, und  als Differenz der Ortsvektoren.
als Differenz der Ortsvektoren.
1 Da sie auf der x-Achse liegen und symmetrisch zum Ursprung sind, liegt der Mittelpunkt bei  und die Gleichung lautet wie folgt
und die Gleichung lautet wie folgt

Wir berechnen den Wert für  , der dem Abstand zwischen dem Mittelpunkt und einem der Brennpunkte entspricht
, der dem Abstand zwischen dem Mittelpunkt und einem der Brennpunkte entspricht
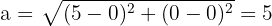
2 Da die Differenz der Ortsvektoren  ist, gilt
ist, gilt  und somit
und somit 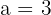
3 Wir berechnen den Wert für 

4 4 Die Gleichung der Hyperbel lauet
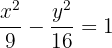
5 Die Exzentrizität ist

Bestimme die Koordinaten der Scheitelpunkte und der Brennpunkte, die Gleichungen der Asymptoten und die Exzentrizität der Hyperbel 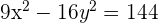 .
.
1 Als Erstes vereinfachen wir die Gleichung. Dazu dividieren wir beide Seiten durch 
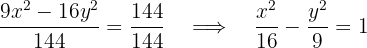
Somit gilt  und
und 
2 Wir berechnen den Wert für 
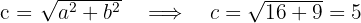
3 Die Koordinaten der Scheitelpunkte lauten
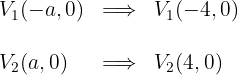
4 Die Koordinaten der Brennpunkte lauten

5 Die Gleichungen der Asymptoten lauten
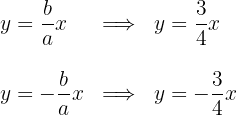
6 Die Exzentrizität ist
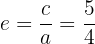
Bestimme die Gleichung der Hyperbel mit dem Brennpunkt  , dem Scheitelpunkt
, dem Scheitelpunkt  und dem Mittelpunkt
und dem Mittelpunkt  .
.
1 Da der Mittelpunkt und der Scheitelpunkt auf der y-Achse liegen, hat die Gleichung folgende Form

Wir berechnen den Wert für  , der dem Abstand zwischen dem Mittelpunkt und einem der Brennpunkte entspricht
, der dem Abstand zwischen dem Mittelpunkt und einem der Brennpunkte entspricht

2 Wir berechnen den Wert für  , der dem Abstand zwischen dem Mittelpunkt und einem der Brennpunkte entspricht
, der dem Abstand zwischen dem Mittelpunkt und einem der Brennpunkte entspricht

3 Wir berechnen den Wert für 

4 Die Gleichung der Hyperbel lauet

Bestimme die Gleichung der Hyperbel mit dem Brennpunkt  , dem Scheitelpunkt
, dem Scheitelpunkt  und dem Mittelpunkt
und dem Mittelpunkt  .
.
1 Da der Mittelpunkt und der Scheitelpunkt die gleiche  -Koordinate haben, hat die Gleichung folgende Form
-Koordinate haben, hat die Gleichung folgende Form
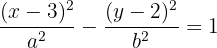
Wir berechnen den Wert für  , der dem Abstand zwischen dem Mittelpunkt und einem der Scheitelpunkte entspricht
, der dem Abstand zwischen dem Mittelpunkt und einem der Scheitelpunkte entspricht
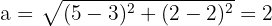
2 Wir berechnen den Wert für  , der dem Abstand zwischen dem Mittelpunkt und einem der Brennpunkte entspricht
, der dem Abstand zwischen dem Mittelpunkt und einem der Brennpunkte entspricht
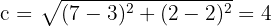
3 Wir berechnen den Wert für 

4 Die Gleichung der Hyperbel lauet
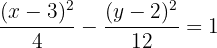
Bestimme die Gleichung der Hyperbel mit dem Brennpunkt  , dem Scheitelpunkt
, dem Scheitelpunkt  und dem Mittelpunkt
und dem Mittelpunkt  .
.
1 Da der Mittelpunkt und der Scheitelpunkt die gleiche  -Koordinate haben, hat die Gleichung folgende Form
-Koordinate haben, hat die Gleichung folgende Form
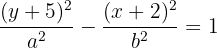
Wir berechnen den Wert für  , der dem Abstand zwischen dem Mittelpunkt und einem der Scheitelpunkte entspricht
, der dem Abstand zwischen dem Mittelpunkt und einem der Scheitelpunkte entspricht
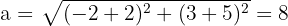
2 Wir berechnen den Wert für  , der dem Abstand zwischen dem Mittelpunkt und einem der Brennpunkte entspricht
, der dem Abstand zwischen dem Mittelpunkt und einem der Brennpunkte entspricht
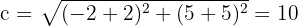
3 Wir berechnen den Wert für 

4 Die Gleichung der Hyperbel lauet
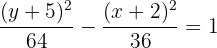
Stelle grafisch dar und bestimme die Koordinaten der Brennpunkte, der Scheitelpunkte und die Exzentrizität der folgenden Hyperbeln:

1 Für die erste Hyperbel der Gleichung haben wir die Werte für 
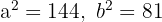 y
y 
2 Wir berechnen den Wert für 

3 Die Hauptachse verläuft horizontal und die Hyperbel hat ihren Mittelpunkt im Ursprung. Daher lauten die Koordinaten der Scheitelpunkte wie folgt
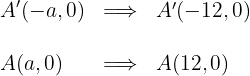
4 Die Koordinaten der Brennpunkte sind
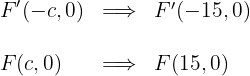
5 Die Exzentrizität ist

6 Grafische Darstellung
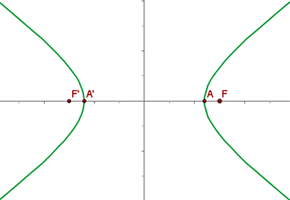
Stelle grafisch dar und bestimme die Koordinaten der Brennpunkte, der Scheitelpunkte und die Exzentrizität der folgenden Hyperbeln:
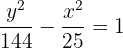
1 Für die zweite Hyperbel der Gleichung haben wir die Werte für 
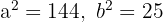 y
y 
2 Wir berechnen den Wert für 

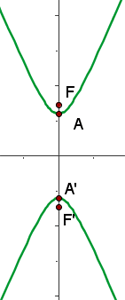
3 Die Hauptachse verläuft vertikal und der Mittelpunkt der Hyperbel liegt im Ursprung. Die Koordinaten der Scheitelpunkte sind also
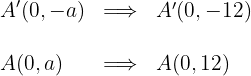
4 Die Koordinaten der Brennpunkte sind
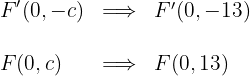
5 Die Exzentrizität ist

6 Grafische Darstellung
Stelle grafisch dar und bestimme die Brennpunkte, die Scheitelpunkte und die Exzentrizität der folgenden Hyperbeln:
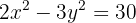
1 Wir vereinfachen die Gleichung für die erste Hyperbel, indem wir beide Seiten durch  dividieren
dividieren
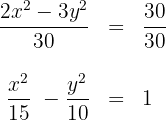
Wir erhalten aus der Gleichung die Werte für  und den Mittelpunkt
und den Mittelpunkt
 und
und 
2 Wir berechnen den Wert für 
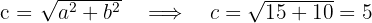
3 Die Hauptachse verläuft horizontal und der Mittelpunkt der Hyperbel liegt im Ursprung. Die Koordinaten der Scheitelpunkte sind also
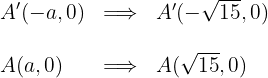
4 Die Koordinaten der Brennpunkte sind
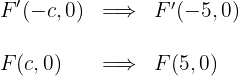
5 Die Exzentrizität ist
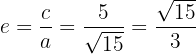
6 Grafische Darstellung
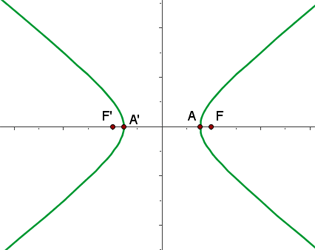
Stelle grafisch dar und bestimme die Brennpunkte, die Scheitelpunkte und die Exzentrizität der folgenden Hyperbeln:
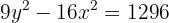
1 Für die zweite Gleichung vereinfachen wir die Gleichung, indem wir beide Seiten durch 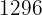 dividieren
dividieren
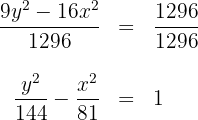
Aus der Gleichung erhalten wir die Werte für  und den Mittelpunkt
und den Mittelpunkt
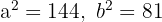 y
y 
2 Wir berechnen den Wert für 

3 Die Hauptachse verläuft vertikal und der Mittelpunkt der Hyperbel liegt im Ursprung. Die Koordinaten der Scheitelpunkte sind also
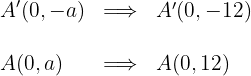
4 Die Koordinaten der Brennpunkte sind
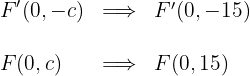
5 Die Exzentrizität ist

6 Grafische Darstellung
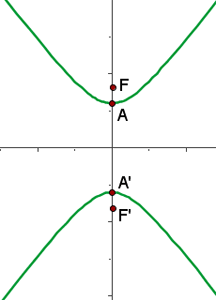
Stelle grafisch dar und bestimme die Koordinaten der Brennpunkte, der Scheitelpunkte und die Exzentrizität der folgenden Hyperbeln:
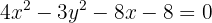
1 Für die erste Hyperbel vereinfachen wir ihre Gleichung
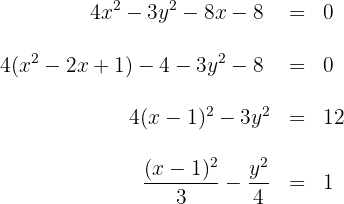
Aus der Gleichung erhalten wir die Werte für  und den Mittelpunkt
und den Mittelpunkt
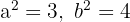 und
und 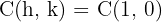
2 Wir berechnen den Wert für 
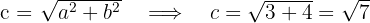
3 Die Hauptachse verläuft horizontal und der Mittelpunkt der Hyperbel liegt bei 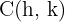 . Die Koordinaten der Scheitelpunkte lauten also
. Die Koordinaten der Scheitelpunkte lauten also
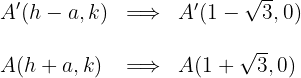
4 Die Koordinaten der Brennpunkte sind

5 Die Exzentrizität ist
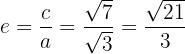
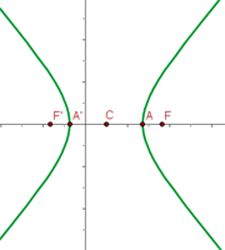
6 Grafische Darstellung
Stelle grafisch dar und bestimme die Koordinaten der Brennpunkte, der Scheitelpunkte und die Exzentrizität der folgenden Hyperbeln:

1 Für die zweite Hyperbel vereinfachen wir ihre Gleichung

Aus der Gleichung erhalten wir die Werte für  und den Mittelpunkt
und den Mittelpunkt
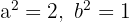 und
und 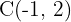
2 Wir berechnen den Wert für 
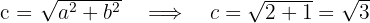
3 Die Hauptachse verläuft horizontal und der Mittelpunkt der Hyperbel liegt bei 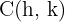 . Die Koordinaten der Scheitelpunkte sind also
. Die Koordinaten der Scheitelpunkte sind also

4 Die Koordinaten der Brennpunkte sind

5 Die Exzentrizität ist
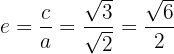
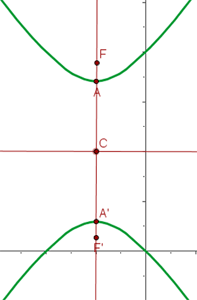
6 Grafische Darstellung
Bestimme die Gleichung einer Hyperbel mit horizontaler Achse von  und der Brennstrecke
und der Brennstrecke  .
.
1 Da die Hauptachse 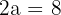 entspricht, gilt
entspricht, gilt 
2 Für die Brennstrecke gilt  , somit
, somit 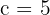
3 Wir berechnen den Wert für 
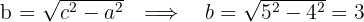
4 Da sich der Mittelpunkt im Ursprung befindet, lautet die Gleichung der Hyperbel

Die Hauptachse einer Hyperbel ist  und verläuft horizontal, der Mittelpunkt liegt im Ursprung und sie verläuft durch den Punkt
und verläuft horizontal, der Mittelpunkt liegt im Ursprung und sie verläuft durch den Punkt  . Bestimme ihre Gleichung.
. Bestimme ihre Gleichung.
1 Für die Hauptachse gilt  , somit
, somit 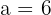
2 Die Gleichung der Hyperbel lauet

3 Da die Hyperbel durch den Punkt  verläuft, setzen wir ein und berechnen den Wert für
verläuft, setzen wir ein und berechnen den Wert für 

4 Da sich der Mittelpunkt im Ursprung befindet, lautet die Gleichung der Hyperbel
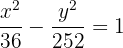
Berechne die Gleichung der Hyperbel, deren Mittelpunkt im Ursprung liegt und deren Hauptachse horizontal verläuft. Die Brennstrecke beträgt 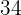 und der Abstand von einem Brennpunkt zum nächstgelegenen Scheitelpunkt
und der Abstand von einem Brennpunkt zum nächstgelegenen Scheitelpunkt  .
.
1 Da die Brennstrecke  entspricht, gilt
entspricht, gilt 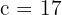
2 Da der Abstand von einem Brennpunkt zum nächstgelegenen Scheitelpunkt 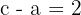 beträgt, gilt
beträgt, gilt 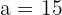
3 Wir berechnen 
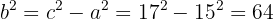
4 Da sich der Mittelpunkt im Ursprung befindet, lautet die Gleichung der Hyperbel
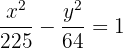
Die Hauptachse einer Hyperbel ist horizontal und misst  , die Exzentrizität ist
, die Exzentrizität ist  . Berechne die Gleichung der Hyperbel.
. Berechne die Gleichung der Hyperbel.
1 Da die Hauptachse  ist, gilt
ist, gilt 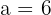
2 Da die Exzentrizität 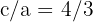 ist, gilt
ist, gilt 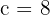
3 Wir berechnen 
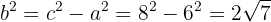
4 Da sich der Mittelpunkt im Ursprung befindet, lautet die Gleichung der Hyperbel
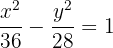
Berechne die Gleichung der gleichseitigen Hyperbel mit der Brennstrecke  .
.
1 Da die Brennstrecke  ist, gilt
ist, gilt 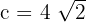
2 Da die Hyperbel gleichseitig ist, gilt  und somit
und somit

3 Da sich der Mittelpunkt im Ursprung befindet, lautet die Gleichung der Hyperbel

Die Nebenachse einer Hyperbel verläuft vertikal und misst  . Die Gleichungen der Aymptoten sind
. Die Gleichungen der Aymptoten sind 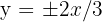 . Berechne die Gleichung der Hyperbel, ihre Achsen, Brennpunkte und Scheitelpunkte.
. Berechne die Gleichung der Hyperbel, ihre Achsen, Brennpunkte und Scheitelpunkte.
1 Für die Nebenachse gilt  . Somit
. Somit 
2 Die Steigung der Asymptoten beträgt 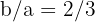 . Somit
. Somit 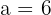
3 Wir berechnen 

4 Da sich der Mittelpunkt im Ursprung befindet, lautet die Gleichung der Hyperbel
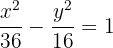
5 Die Koordinaten der Scheitelpunkte sind
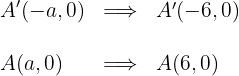
6 Die Koordinaten der Brennpunkte lauten
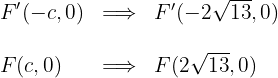
Bestimme die Gleichung der Hyperbel mit horizontaler Hauptachse, deren Mittelpunkt im Ursprung liegt und die durch die Punkte 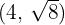 und
und 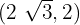 verläuft.
verläuft.
1 Die Gleichung der Hyperbel hat die Form

2 Da die Hyperbel durch die Punkte 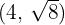 und
und 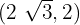 verläuft, erhalten wir durch Substitution ein Gleichungssystem in Form von
verläuft, erhalten wir durch Substitution ein Gleichungssystem in Form von 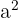 und
und 
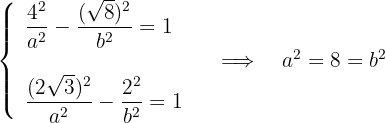
3 Die Gleichung der Hyperbel lauet
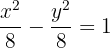
Bestimme die Gleichung der Hyperbel mit horizontaler Hauptachse, deren Mittelpunkt im Ursprung liegt, die durch den Punkt  verläuft und deren Exzentrizität
verläuft und deren Exzentrizität 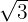 ist.
ist.
1 Die Gleichung der Hyperbel hat die Form

2 Da die Hyperbel durch den Punkt  verläuft, setzen wir ein und erhalten
verläuft, setzen wir ein und erhalten
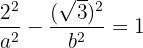
3 Für die Exzentrizität gilt 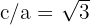 und
und 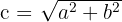 . Wir setzen wir ein und erhalten
. Wir setzen wir ein und erhalten

4 Wir haben ein Gleichungssystem, aus dem sich Folgendes ergibt
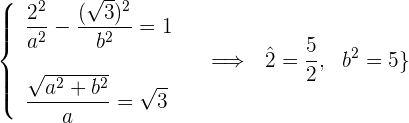
5 Die Gleichung der Hyperbel lautet

Bestimme die Gleichung der Hyperbel, deren Mittelpunkt im Ursprung liegt und deren Hauptachse horizontal verläuft. Außerdem beträgt der Abstand zwischen einem Brennpunkt und den Scheitelpunkten der Hyperbel  und
und  .
.
1 Aus den angegegeben Werten ergibt sich für die Hauptachse 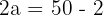 . Somit gilt
. Somit gilt 
2 Die Brennstrecke entspricht 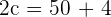 . Somit gilt
. Somit gilt 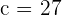
3 Wir berechnen den Wert für 
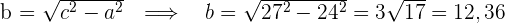
4 Da sich der Mittelpunkt im Ursprung befindet, lautet die Gleichung der Hyperbel
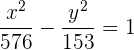
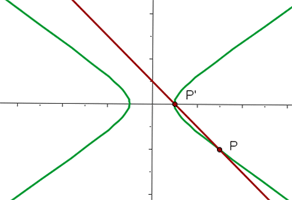
Bestimme die relative Lage der Geraden 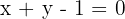 in Bezug auf die Hyperbel
in Bezug auf die Hyperbel 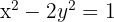 .
.
1 Wir bestimmen die Schnittpunkte der beiden Kurven. Hierzu bestimmen wir die Variable  der Geraden
der Geraden 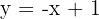 und setzen in die Hyperbel ein
und setzen in die Hyperbel ein

Wir erhalten  und
und 
2 Wir setzen die Werte für  in die Gleichung der Geraden ein und erhalten die Schnittpunkte
in die Gleichung der Geraden ein und erhalten die Schnittpunkte 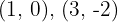
3 Grafische Darstellung
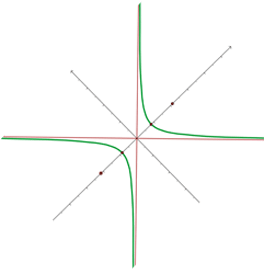
Eine gleichseitige Hyperbel verläuft durch den Punkt 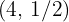 . Bestimme ihre Gleichung mit den Asymptoten als Achsen und die Koordinaten der Scheitelpunkte.
. Bestimme ihre Gleichung mit den Asymptoten als Achsen und die Koordinaten der Scheitelpunkte.
1 Wir bestimmen die Gleichung der Hyperbel. Hierzu multiplizieren wir 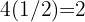 . Somit lautet die Gleichung der gleichseitigen Hyperbel
. Somit lautet die Gleichung der gleichseitigen Hyperbel 
2Da die Hyperbel gleichseitig ist, ist 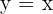 die Gerade, die auf der Hauptachse liegt. Die Scheitelpunkte erhalten wir durch das Lösen der Gleichungssysteme
die Gerade, die auf der Hauptachse liegt. Die Scheitelpunkte erhalten wir durch das Lösen der Gleichungssysteme

3 Grafische Darstellung
Mit KI zusammenfassen:



