Kapitel
Quadratische Funktion
Polynomfunktionen sind Funktionen, die aus einem Polynom bestehen. Ein Beispiel hierfür ist die quadratische Funktion, die durch eine Parabel und die folgende Gleichung dargestellt wird:
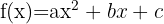
Grafische Darstellung der Parabel
Um ein Parabeldiagramm zu erstellen, musst Du die folgenden Elemente kennen:
Scheitelpunkt
Die Symmetrieachse der Parabel verläuft durch den Scheitelpunkt, d. h. wenn der Koeffizient des Terms 
positiv ist, ist der Scheitelpunkt der tiefste Punkt des Graphen. Die Formeln, um ihn zu finden, sind die folgenden:
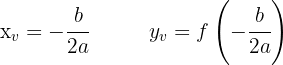
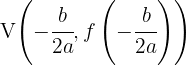
Die Gleichung der Symmetrieachse lautet ebenfalls:
Schnittpunkte auf der X-Achse
Um den Wert von 
zu finden, wenn 
ist, muss die zweite Koordinate gleich Null sein. Also musst Du die folgende Gleichung lösen:
Die Lösung der obigen Gleichung führt zu folgenden Ergebnissen:
- Zwei Schnittpunkte:
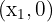und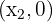 
dies geschieht, wenn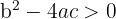 
- Ein Schnittpunkt: 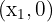dies geschieht, wenn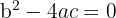
- Kein Schnittpunkt, wenn
Schnittpunkt mit der Y-Achse
Um den Schnittpunkt mit der 
-Achse zu finden, muss die erste Koordinate gleich Null sein, 
, also hast Du:
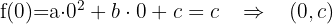
Beispiel
Um die Funktion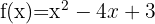 
darzustellen, musst Du die folgenden Elemente finden, aus denen die Parabel besteht:
Scheitelpunkt
Wende die im vorigen Abschnitt beschriebenen Formeln an, um die Koordinaten des Scheitelpunkts zu ermitteln, die wie folgt lauten
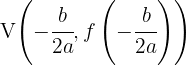
Die Koordinaten des Scheitelpunkts sind dann: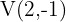 
Schnittpunkte auf der X-Achse
Um den oder die Schnittpunkte mit der x-Achse zu finden, setzt Du die Funktion, wie oben angegeben, mit 0 gleich:
Um die Gleichung zu lösen, wird die abc-Formel für quadratische Gleichungen verwendet:
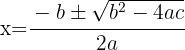
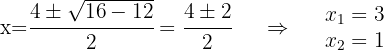
In diesem Fall hast Du zwei Schnittpunkte gefunden, die lauten: 
y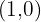 
Schnittpunkt mit der Y-Achse
Um den Schnittpunkt mit zu finden, genügt es, den Wert der Konstante 
zu kennen, der in diesem Fall 
ist, und die Koordinaten sind: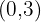 
.
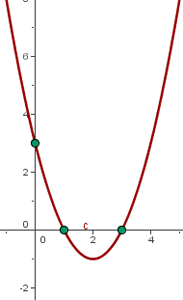
Graph der quadratischen Funktion
Du gehst von 
aus
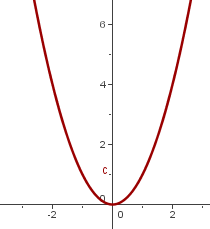
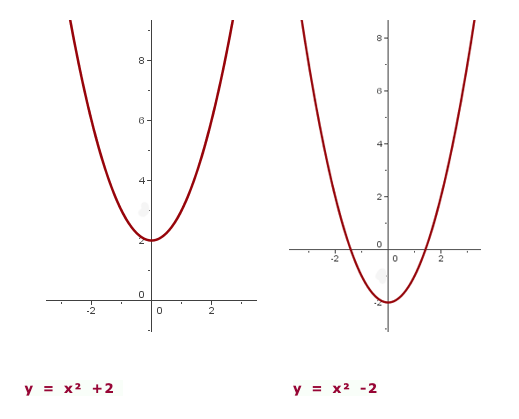
Vertikale Verschiebung
Wenn Deine Funktion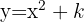 
ist
Wobei:
, dann verschiebt sich um 
Einheiten nach oben.
, dann verschiebt sich um Einheiten nach unten.
In diesem Fall ist der Scheitelpunkt der Parabel: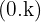 
.
Und die Symmetrieachse .
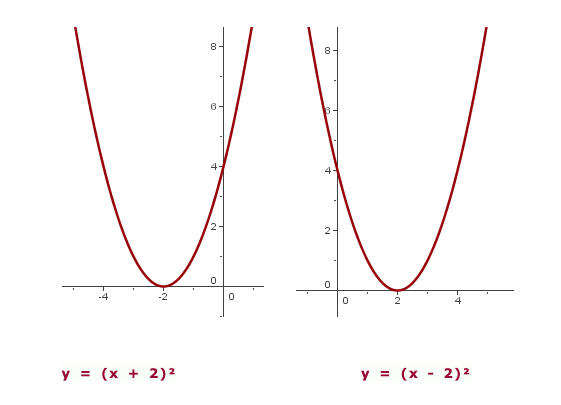
Horizontale Verschiebung
Für die Gleichung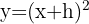 
Wobei:
- Wenn
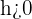, dann ist um 
Einheiten nach links verschoben. - Wenn
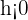, dann ist um Einheiten nach rechts verschoben.
In dieser Übung ist der Scheitelpunkt der Parabel: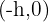 
.
Und die Symmetrieachse ist 
.
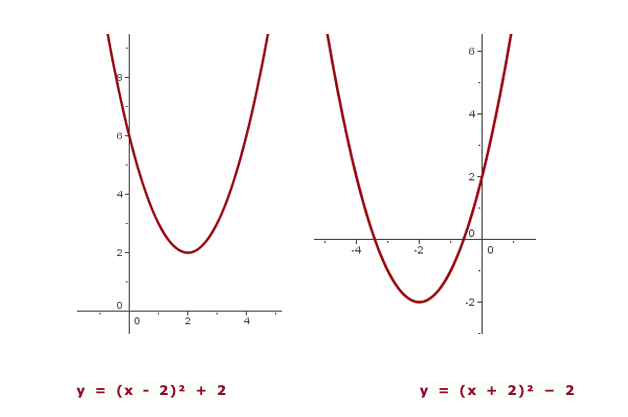
Schräge Verschiebung
Schließlich ist in der folgenden Gleichung 
, der Scheitelpunkt der Parabel: 
.
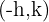Und die Symmetrieachse ist .
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
