Kapitel
Eine rationale Funktion ist durch einen Quotienten von Polynomen gegeben:
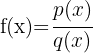
mit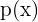 
und 
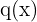Polynomen, die keinen gemeinsamen Faktor haben.
Es ist praktisch festzustellen, dass jede Polynomfunktion eine rationale Funktion ist, man denke nur an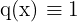 
; eine rationale Funktion ist jedoch nicht immer polynomial.
Beispiel: die umgekehrten Proportionalitätsfunktionen der Gleichung:
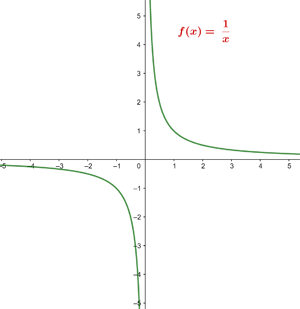
Die Graphen sind Hyperbeln. Die Graphen der folgenden Funktionen sind ebenfalls Hyperbeln:
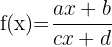
mit 
Definitionsbereich rationaler Funktionen
Im Gegensatz zu Polynomfunktionen, deren Definitionsbereich alle reellen Zahlen 
sind, sind rationale Funktionen auf allen 
-Werten definiert, bei denen der Nenner 
ist. Das heißt:
Beispiel: Für die rationale Funktion
,
haben wir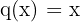 
, weshalb der Definitionsbereich
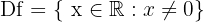ist.
In Intervallen ausgedrückt:
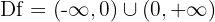
Asymptoten
Die Werte , für die der Nenner der rationalen Funktion 0 ist, ergeben die vertikalen Asymptoten. Die vertikalen Asymptoten sind also die Geraden 
, für die gilt, dass
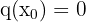
Zur Berechnung der schiefen Asymptoten 
nutzen wir
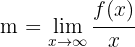
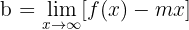
Beispiel: Gegeben ist die rationale Funktion
Wir berechnen die vertikalen Asymptoten, für die wir die Werte suchen, durch die der Nenner 0 wird.
Wir berechnen die schiefen Asymptoten, für die wir Folgendes suchen
Es handelt sich also um eine horizontale Asymptote, die wie folgt ist
Schnittpunkte mit den Koordinatenachsen
Um die Schnittpunkte mit der x-Achse zu ermitteln, müssen wir die Funktion gleich 0 setzen und die Werte von berechnen. Also 
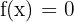
Um den Schnittpunkt mit der y-Achse zu berechnen, werten wir die Funktion für aus. Also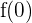 
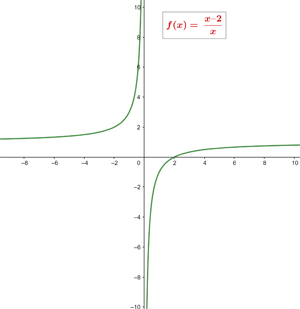
Beispiel: Gegeben ist die rationale Funktion
Sie hat keine Schnittpunkte mit den Koordinatenachsen, da diese Asymptoten der Funktion sind
Grenzwerte – Unendlichkeitsbereich
Um das Verhalten im Unendlichen zu bestimmen, genügt es, die folgenden Grenzwerte zu berechnen
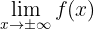
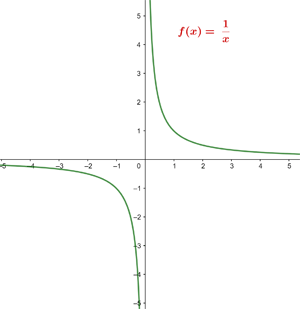
Beispiel: Die Funktion
gegen Unendlich ist
so dass die Funktion im Unendlichen gegen 0 konvergiert, d. h. die Höhe des Graphen geht gegen 0, was aus dem Graphen der Funktion ersichtlich ist
Stetigkeit
Wenn der Nenner 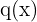für einen beliebigen Wert nicht 0 wird, ist die Funktion in all ihren Punkten stetig.
Die Werte für die 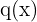0 wird, sind die Punkte, in denen die rationale Funktion nicht stetig ist. Das heißt, die rationale Funktion ist an den vertikalen Asymptoten nicht stetig..
Beispiel: Die rationale Funktion
ist nicht stetig in
Kritische Punkte
Diese Punkte erhält man durch Ableitung der rationalen Funktion und Gleichsetzung mit 0. Die Werte, bei denen sich die Ableitung aufhebt, werden als kritische Punkte bezeichnet. An diesen Punkten kann die Funktion ihr relatives Maximum oder Minimum erreichen.
Nicht alle rationalen Funktionen haben Maxima und Minima in ihrem Definitionsbereich.
Beispiel: Die Funktion
hat keine Maxima oder Minima in ihrem Definitionsbereich
Hierfür berechnen wir die Ableitung
Sie wird nicht 0 im Definitionsbereich der Funktion, weshalb die Funktion keine Maxima und keine Minima in ihrem Definitionsbereich hat.
Aufgaben zu rationalen Funktionen
Ermittlung des Graphen, des Definitionsbereichs, der Asymptoten, der Schnittpunkte mit den Koordinatenachsen, des Verhaltens im Unendlichen, der Stetigkeit und der kritischen Punkte von rationalen Funktionen
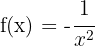
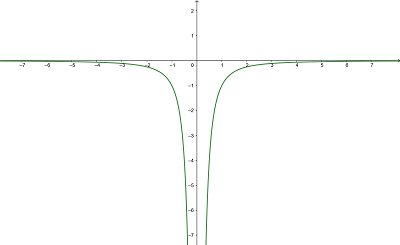
1 Der Graph der Funktion ist
2 Definitionsbereich der Funktion
Wir haben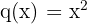 
. Der Definitionsbereich lautet also
,
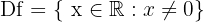que expresado en intervalos es
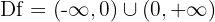
3 Asymptoten
Wir berechnen die vertikalen Asymptoten, für die wir die Werte suchen, durch die der Zähler 0 wird. Die vertikale Asymptote ist also
Wir berechnen die schiefen Asymptoten, für die wir Folgendes suchen
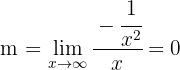
Es handelt sich also um eine horizontale Asymptote:
4 Schnittpunkte mit den Koordinatenachsen
es gibt keine Schnittpunkte mit den Koordinatenachsen, da diese Asymptoten der Funktion sind
5 Verhalten im Bereich der Unendlichkeit
Wir berechnen
Die Funktion konvergiert also im Unendlichkeitsbereich gegen 0; die Höhe des Graphen geht gegen 0, was aus dem Graphen der Funktion ersichtlich ist
6 Stetigkeit
Die Funktion hat eine vertikale Asymptote in
somit ist die Funktion nicht stetig in
7 Kritische Punkte
Die Funktion hat keine Maxima und Minima in ihrem Definitionsbereich
Hierfür benötigen wir die Ableitung
Diese wird im Definitionsbereich der Funktion nicht 0. Die Funktion hat somit keine Minima und keine Maxima in ihrem Definitionsbereich.
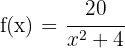
1 Der Graph der Funktion ist
2 Definitionsbereich der Funktion
Wir haben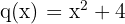 
la cual nunca se anula en los números reales por lo que su dominio es
,
In Intervallen ausgedrückt
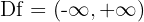
3 Asymptoten
Wir berechnen die vertikalen Asymptoten, für die wir die Werte suchen, durch die der Zähler 0 wird. Da der Zähler niemals 0 ist, gibt es keine vertikalen Asymptoten.
Wir berechnen die schiefen Asymptoten, für die wir Folgendes suchen
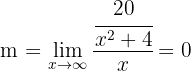
Es handelt sich somit um eine horizontale Asymptote:
4 Schnittpunkte mit den Koordinatenachsen
Es gibt keine Schnittpunkte mit der x-Achse, da diese eine Asymptote der Funktion ist
Der Schnittpunkt mit der y-Achse ist
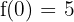
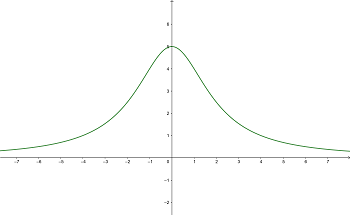
5 Verhalten im Unendlichkeitsbereich
Wir berechnen
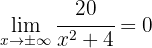
so dass die Funktion im Unendlichen gegen 0 konvergiert, d. h. die Höhe des Graphen geht gegen 0, was aus dem Graphen der Funktion ersichtlich ist
6 Stetigkeit
Die Funktion hat keine vertikale Asymptote und ist daher im gesamten Definitionsbereich stetig
7 Kritische Punkte
Wir berechnen die Ableitung
Wir setzen die Ableitung gleich 0 und erhalten so den kritischen Punkt
Wir berechnen die 2. Ableitung
Wir werten den kritischen Punkt in der 2. Ableitung aus
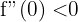
Die Funktion hat also ein Maximum bei
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
