Kapitel

 

Regel von L'Hôpital

Wenn und zwei stetige Funktionen sind, für die gilt

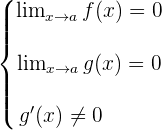
Die Regel von L'Hôpital besagt, dass

 .

Um die Regel von L'Hôpital anwenden zu können, muss man einen Grenzwert der Form haben, und eine der folgenden Unbestimmtheiten aufweisen

  • ,

Hier findest Du einige gelöste Übungen, die Dir helfen, die Zusammenhänge besser zu verstehen

Gelöste Aufgaben der L'Hôpital-Regel

1

Lösung

1 Identifizierung der Unbestimmtheit

2 Anwendung der L'Hôpital-Regel

Leite den Zähler und den Nenner des Quotienten ab. Setze Grenzwerte.

3 Ermittle den Grenzwert

2

Lösung

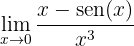
1 Identifizierung der Unbestimmtheit

2 Anwendung der L'Hôpital-Regel

Leite den Zähler und den Nenner des Quotienten ab. Setze Grenzwerte.

Auch hier ergibt sich eine Unbestimmtheit, so dass wir erneut die L'Hôpital-Regel anwenden

Noch einmal

3 Ermittle den Grenzwert

3

Lösung

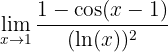
1 Identifizierung der Unbestimmtheit

2 Anwendung der L'Hôpital-Regel

Leite den Zähler und den Nenner des Quotienten ab. Setze Grenzwerte.

Wende die Regel erneut an

3 Ermittle den Grenzwert

4

Lösung

1 Identifizierung der Unbestimmtheit

2 Anwendung der L'Hôpital-Regel

Leite den Zähler und den Nenner des Quotienten ab. Setze Grenzwerte.

Verwende die folgende Eigenschaft der trigonometrischen Funktionen und wende erneut die Regel von L'Hôpital an

3 Ermittle den Grenzwert

Unbestimmte Formen von Potenzen

Die unbestimmten Formen , und  erhält man, wenn man folgende Ausdrücke der Form hat:

Diese Unbestimmtheiten werden zunächst durch Anwendung der Eigenschaften des Logarithmus gelöst:

Du hast Deine Funktion

Wende den Logarithmus an

Verwende eine exponentielle Funktion

Dann

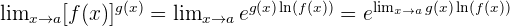
Um den Anfangsgrenzwert zu bestimmen, genügt es also, den Grenzwert des Logarithmus zu ermitteln

Der ursprüngliche Grenzwert wird also sein

Lösungsaufgaben mit Unbestimmtheiten

1

Lösung

1 Identifizierung der Unbestimmtheit

2 Nimm den Grenzwert des Logarithmus

Du hast eine unvollständige Form

3 Anwendung der L'Hôpital-Regel

Unvollständige Form

Wende erneut die Regel von L'Hôpital an

4 Erhalte den Grenzwert

Deshalb

Und dann

2

Lösung

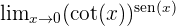
1 Identifizierung der Unbestimmtheit

2 Nimm den Grenzwert des Logarithmus

Du hast eine unbestimmte Form

3 Anwendung der L'Hôpital-Regel

Durch Ableitung erhältst Du

Dann

4 Du erhältst den ursprünglichen Grenzwert

Deshalb

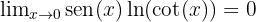
Und dann

3

Lösung

1 Identifizierung der Unbestimmtheit

2 Nimm den Grenzwert des Logarithmus

Du hast eine unbestimmte Form

3 Anwendung der L'Hôpital-Regel

Durch Ableitung erhältst Du

Dann

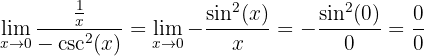
Wende die Regel von L'Hôpital erneut an

4 Du erhältst den ursprünglichen Grenzwert

Deshalb

Und dann

4

Lösung

1 Identifizierung der Unbestimmtheit

2 Berechne den Grenzwert des Logarithmus

Du hast eine unvollständige Form

3 Anwendung der L'Hôpital-Regel

Durch Ableitung erhältst Du

4 Du erhältst den ursprünglichen Grenzwert

Deshalb:

Und dann

Lösungsaufgaben zur Unbestimmtheit unendlich minus unendlich

In diesen Fällen musst Du beachten, wie "schnell" die Funktionen ins Unendliche gehen. Wenn es sich um Brüche handelt, werden sie außerdem auf einen gemeinsamen Nenner gebracht.

1

Lösung

1 Identifizierung der Unbestimmtheit

2 Schreibe den Ausdruck um

3 Anwendung der L'Hôpital-Regel

Durch Ableitung erhältst Du

Du erhältst eine weitere Unbestimmtheit, also wendest Du die Regel erneut an

4 Erhalte den Grenzwert

Deshalb

2

Lösung

1 Identifizierung der Unbestimmtheit

2 Schreibe den Ausdruck um

3 Anwendung der L'Hôpital-Regel

Durch Ableitung erhältst Du

Du erhältst eine weitere Unbestimmtheit, also wendest Du die Regel erneut an

4 Erhalte den Grenzwert

Deshalb

Unbestimmte Null durch Unendlichkeit

Diese Formen der Unbestimmtheit können in bereits bekannte Fälle wie ó .

Wie unten dargestellt, musst Du

wobei und

Dann kannst Du es so umschreiben, dass es einfacher ist, die Ableitung herauszunehmen

oder

Damit kannst Du nun die L'Hôpital-Regel anwenden

 

Lösungsaufgaben zur unbestimmten Null durch Unendlichkeit

1

Lösung

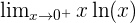
1 Identifizierung der Unbestimmtheit

2 Schreibe den Ausdruck um

Unbestimmtheit vom Typ

3 Anwendung der L'Hôpital-Regel

Durch Ableitung erhältst Du

4 Erhalte den Grenzwert

Deshalb:

2

Lösung

1 Identifizierung der Unbestimmtheit

2 Schreibe den Ausdruck um

Um die L'Hôpital-Regel anwenden zu können, drückst Du das Gleiche auf eine bequeme Weise aus

3 Anwendung der L'Hôpital-Regel

Durch Ableitung erhältst Du

4 Erhalte den Grenzwert

Deshalb:

Verschiedene Übungen zu Unbestimmtheiten und der Regel L'Hôpital

1

Lösung

1 Identifizierung der Unbestimmtheit

2 Anwendung der L'Hôpital-Regel

Leite den Zähler und den Nenner des Quotienten ab. Setze Grenzwerte.

3 Ermittle den Grenzwert

2

Lösung

1 Identifizierung der Unbestimmtheit

2 Anwendung der L'Hôpital-Regel

Leite den Zähler und den Nenner des Quotienten ab. Setze Grenzwerte.

3 Ermittle den Grenzwert

3

Lösung

1 Identifizierung der Unbestimmtheit

2 Das Problem neu formulieren

Nur wenn Du die Gleichung umstellst, kannst Du die Bedingungen für die Anwendung der Regel von L'Hôpital finden

3 Anwendung der L'Hôpital-Regel

Leite den Zähler und den Nenner des Quotienten ab. Setze Grenzwerte.

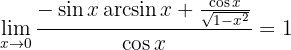
4 Ermittle den Grenzwert

4

Lösung

1 Identifizierung der Unbestimmtheit

2 Berechne den Grenzwert des Logarithmus

Du hast eine unvollständige Form

3 Anwendung der L'Hôpital-Regel

Leite den Zähler und den Nenner des Quotienten ab. Setze Grenzwerte.

4 Ermittle den Grenzwert

5

Lösung

1 Identifizierung der Unbestimmtheit

2 Berechne den Grenzwert des Logarithmus

Du hast eine unvollständige Form

3 Anwendung der L'Hôpital-Regel

Leite den Zähler und den Nenner des Quotienten ab. Setze Grenzwerte.

Erneute Anwendung der L'Hôpital-Regel

4 Ermittle den Grenzwert

6

Lösung

1 Identifizierung der Unbestimmtheit

2 Anwendung der L'Hôpital-Regel

Leite den Zähler und den Nenner des Quotienten ab. Setze Grenzwerte.

Wende erneut die Regel von L'Hôpital an

3 Ermittle den Grenzwert

7

Lösung

1 Identifizierung der Unbestimmtheit

2 Schreibe den Ausdruck um

Unbestimmtheit

3 Anwendung der L'Hôpital-Regel

Wende erneut die Regel von L'Hôpital an

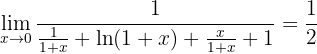
4 Ermittle den Grenzwert

8

Lösung

1 Identifizierung der Unbestimmtheit

2 Nimm den Grenzwert des Logarithmus

Du hast eine unvollständige Form

3 Anwendung der L'Hôpital-Regel

4 Erhalte den ursprünglichen Grenzwert

9

Lösung

1 Identifizierung der Unbestimmtheit

2 Nimm den Grenzwert des Logarithmus

Stelle die Gleichung um

Du hast eine unbestimmte Form

3 Anwendung der L'Hôpital-Regel

Wende erneut die Regel von L'Hôpital an

4 Erhalte den ursprünglichen Grenzwert

Du findest diesen Artikel toll? Vergib eine Note!

4,00 (2 Note(n))
Loading...

Chantal

Sprachen, Literatur, Theater und Musik sind meine große Leidenschaft und waren schon immer ein wichtiger Teil meines schulischen, beruflichen und privaten Werdeganges.