Kapitel

Stetigkeit von Funktionen
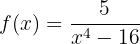
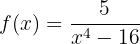
Die Funktion ist an allen Punkten ihres Definitionsbereichs stetig, außer bei den Werten, für die der Nenner null wird.
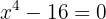

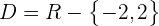
Die Funktion ist an zwei Punkten unstetig:  und
und  .
.
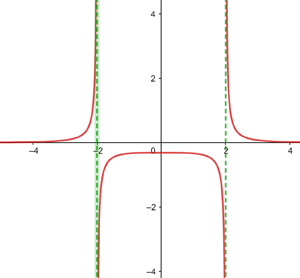
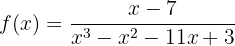
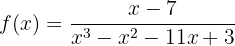
Die Funktion ist im gesamten Definitionsbereich ℛ stetig, außer für die Werte, für die der Nenner null wird. Wenn wir sie gleich null setzen und lösen, erhalten wir die Punkte der Unstetigkeit.

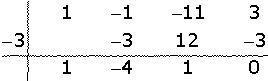
 ; und wenn wir die Gleichung 2. Grades lösen, erhalten wir:
; und wenn wir die Gleichung 2. Grades lösen, erhalten wir:
 und
und 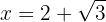
Die Funktion hat drei Punkte der Unstetigkeit bei
 ,
,  y
y 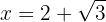
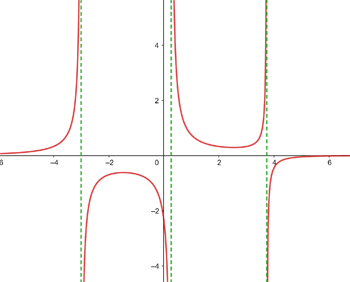
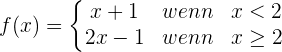
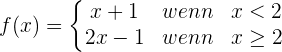
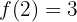
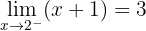
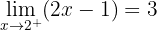
Die Funktion ist im gesamten Definitionsbereich ℛ stetig
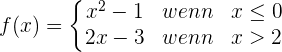
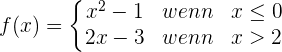

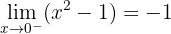

Sprung = 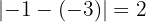
Die Funktion ist unstetig und macht einen Sprung von 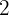 bei
bei  .
.
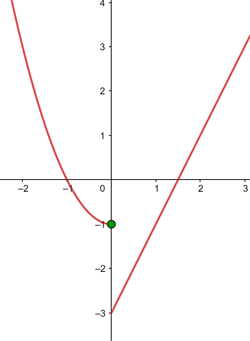
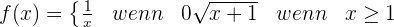
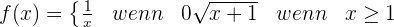
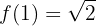
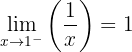
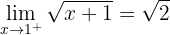
Bei  gibt es eine Unstetigkeitsstelle, eine endliche Sprungstelle
gibt es eine Unstetigkeitsstelle, eine endliche Sprungstelle
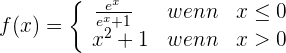
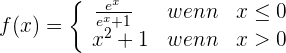
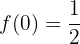


Sprung = 
Die Funktion ist unstetig und macht einen Sprung von  bei
bei  .
.
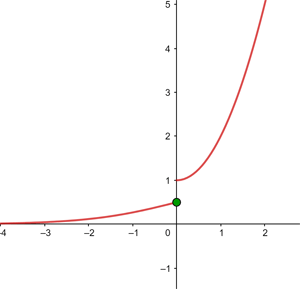
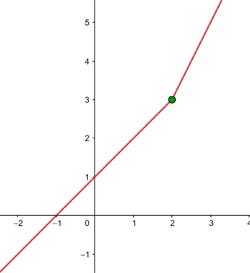
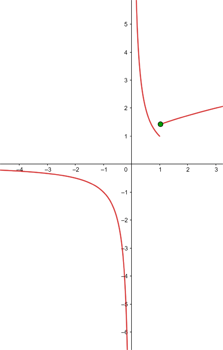
Untersuche die Stetigkeit von f(x) bei x = 0.
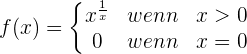
Untersuche die Stetigkeit von f(x) bei x = 0.
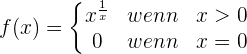
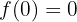
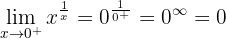
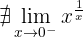
Bei  gibt es eine wesentliche Unstetigkeit.
gibt es eine wesentliche Unstetigkeit.
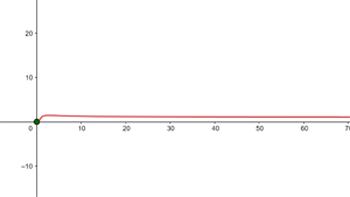
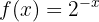
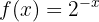

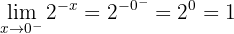

Die Funktion ist bei  stetig
stetig
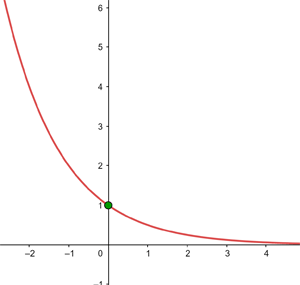
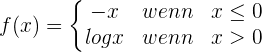
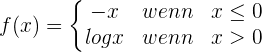
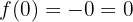
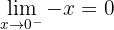
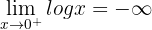
Bei  ist die Funktion unstetig und hat eine unendliche Sprungstelle.
ist die Funktion unstetig und hat eine unendliche Sprungstelle.
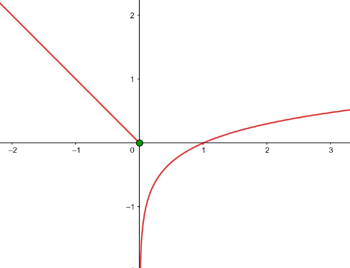
Untersuche die Stetigkeit der Funktion bei x = 0:
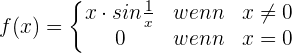
Untersuche die Stetigkeit der Funktion bei x = 0:
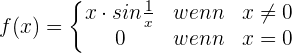
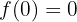
Die Funktion 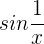 ist beschränkt
ist beschränkt 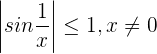 . Wir untersuchen also:
. Wir untersuchen also:
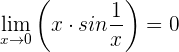
Der Grenzwert ist 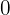 , da jede mit der Zahl Null multiplizierte Zahl null ergibt.
, da jede mit der Zahl Null multiplizierte Zahl null ergibt.
Die Funktion ist im gesamten Definitionsbereich ℛ stetig.
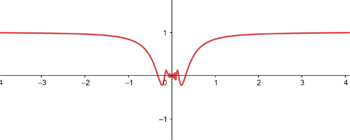
Gegeben ist die Funktion:
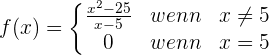
1 Zeige, dass f(x) bei x = 5 unstetig ist.
2 Gibt es eine stetige Funktion, die für alle Werte x ≠ 5 mit f(x) übereinstimmt?
Wenn ja, gib ihren Ausdruck an.
Gegeben ist die Funktion:
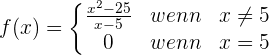
1 Zeige, dass  bei
bei  unstetig ist.
unstetig ist.
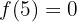
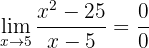
Wir lösen, indem wir den Zähler faktorisieren und vereinfachen: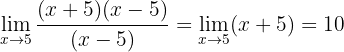
 ist unstetig bei
ist unstetig bei  , da:
, da:

2 Gibt es eine stetige Funktion, die für alle Werte  mit
mit  übereinstimmt?
übereinstimmt?
Wenn ja, gib ihren Ausdruck an.
Wenn 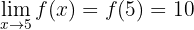 , ist die Funktion stetig. Die neu definierte Funktion lautet:
, ist die Funktion stetig. Die neu definierte Funktion lautet:
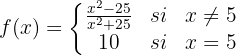
Untersuche die Stetigkeit der Funktion:
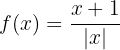
Untersuche die Stetigkeit der Funktion:
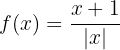
Die Funktion  ist stetig für
ist stetig für 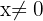 . Wir untersuchen nun die Stetigkeit bei
. Wir untersuchen nun die Stetigkeit bei  .
.

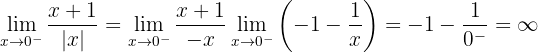
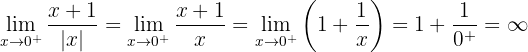
Die Funktion ist bei  unstetig, da sie bei
unstetig, da sie bei  nicht definiert ist, weil der Nenner null wird.
nicht definiert ist, weil der Nenner null wird.
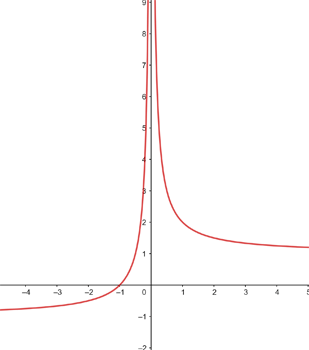
Untersuche die Stetigkeit der Funktion f(x) = x · sgn x
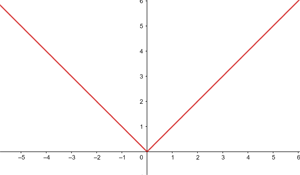
Untersuche die Stetigkeit der Funktion f(x) = x · sgn x.
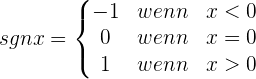
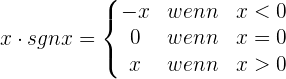
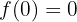
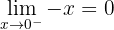
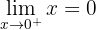
Die Funktion ist im gesamten Definitionsbereich ℛ stetig.
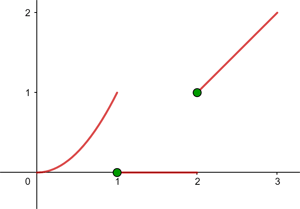
Untersuche die Stetigkeit der Funktion im Intervall (0,3):
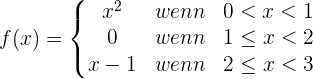
Untersuche die Stetigkeit der Funktion im Intervall (0,3):
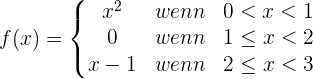
Zweifel an der Stetigkeit der Funktion gibt es nur an den Punkten  und
und  , an denen sich die Form der Funktion ändert.
, an denen sich die Form der Funktion ändert.

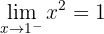

Sprung = 
Bei  ist die Funktion unstetig und macht einen Sprung von
ist die Funktion unstetig und macht einen Sprung von  .
.
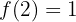
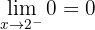
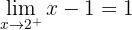
Sprung = 
Bei  ist die Funktion unstetig und macht einen Sprung von
ist die Funktion unstetig und macht einen Sprung von  .
.
Berechne den Wert von a, damit folgende Funktion stetig ist:
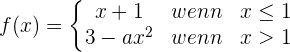
Berechne den Wert von a, damit folgende Funktion stetig ist:
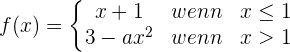
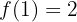
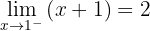
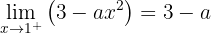
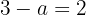
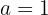
Die folgende Funktion ist definiert durch:
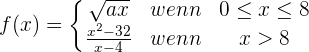
ist stetig bei 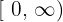 .
.
Ermittle den Wert von a, der diese Aussage wahr macht.
Die folgende Funktion ist definiert durch:
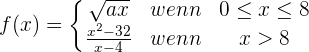
ist stetig bei 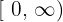 .
.
Ermittle den Wert von a, der diese Aussage wahr macht.
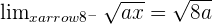
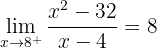

Mit KI zusammenfassen:













