Kapitel

Bestimme die Punkte
Gegeben ist die Parabel . Bestimme die Punkte, in denen die Tangente parallel zur Winkelhalbierenden des 1. Quadranten ist. Bestimme außerdem die Gleichung der Tangente und der Normalen an diesen Punkten.
. Bestimme die Punkte, in denen die Tangente parallel zur Winkelhalbierenden des 1. Quadranten ist. Bestimme außerdem die Gleichung der Tangente und der Normalen an diesen Punkten.
1 Punkte bestimmen
Die Winkelhalbierende des 1. Quadranten hat die Gleichung  und somit ist
und somit ist 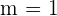 .
.
Wir leiten die Gleichung der Parabel ab, da uns die Ableitung die Steigung angibt
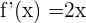
wir setzen gleich  und lösen nach x auf
und lösen nach x auf

Wir werten an diesem Punkt  die ursprüngliche Funktion aus
die ursprüngliche Funktion aus
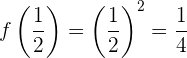
Somit
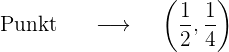
2 Tangente
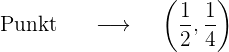
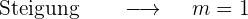
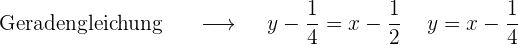
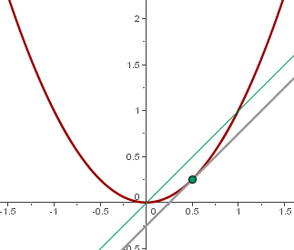
3 Normale
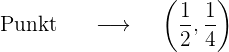
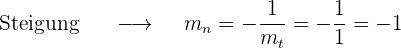
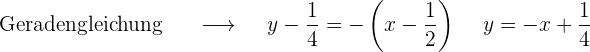
Gegeben ist die Kurve mit der Gleichung  . Bestimme die Koordinaten der Punkte auf dieser Kurve, an denen die Tangente mit der
. Bestimme die Koordinaten der Punkte auf dieser Kurve, an denen die Tangente mit der  -Achse einen Winkel von
-Achse einen Winkel von 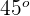 bildet.
bildet.
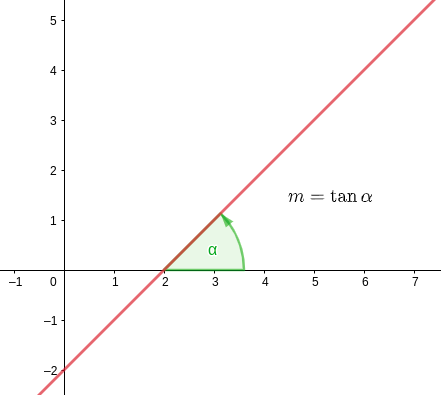
Zunächst muss man wissen, dass die Steigung einer Geraden gleich dem Tangens des Winkels ist, den sie mit der  -Achse bildet.
-Achse bildet.
Das heißt 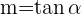
Die Ableitung von  gibt die Steigung der Tangente an
gibt die Steigung der Tangente an
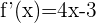
Da die Tangente einen Winkel von 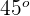 mit der
mit der  -Achse bilden soll, muss die Steigung einen Wert von
-Achse bilden soll, muss die Steigung einen Wert von  haben
haben
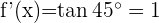
Somit
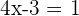
Wir bestimmen
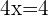
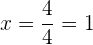
Durch die Ermittlung des Wertes von x haben wir die x-Achse erhalten.Um den Wert der Ordinate zu bestimmen, werten wir den Punkt  in der ursprünglichen Funktion aus
in der ursprünglichen Funktion aus

Zum Schluss
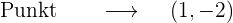
Berechne die Punkte, an denen die Tangente der Kurve 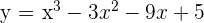 parallel zur
parallel zur  -Achse verläuft.
-Achse verläuft.
Parallele Geraden haben dieselbe Steigung. Die Steigung der  -Achse ist null. Die Tangente an der Kurve soll also dann die Steigung null haben. Es muss gelten
-Achse ist null. Die Tangente an der Kurve soll also dann die Steigung null haben. Es muss gelten
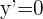
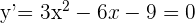
Wir vereinfachen und erhalten die Gleichung

Wir lösen und prüfen die Lösungen in der Funktion 


Schließlich lauten die Punkte, an denen die Tangente der Kurve parallel zur  -Achse ist:
-Achse ist:


Es wurde eine Tangente an die Kurve 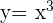 gezeichnet, deren Steigung
gezeichnet, deren Steigung  ist und die durch den Punkt
ist und die durch den Punkt  verläuft. Bestimme den Berührungspunkt.
verläuft. Bestimme den Berührungspunkt.
Die Ableitung gibt die Steigung der Tangente der Kurve an
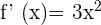
Wir sehen, dass die Steigung  ist und somit
ist und somit
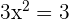
Wir lösen

Wir erhalten die Gleichung der Tangente an diesen Punkten
1 Abszisse x=1
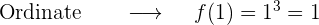
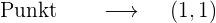
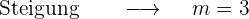
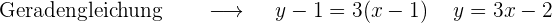
2 Abszisse x=-1
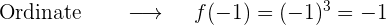
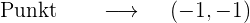
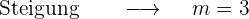
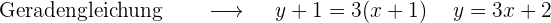
Der Punkt  gehört jedoch nur zu der Geraden
gehört jedoch nur zu der Geraden  .
.
Der Berührungspunkt ist somit 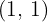
Ermittele die Punkte der Kurve  an denen die Tangente einen Winkel von
an denen die Tangente einen Winkel von 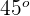 mit der
mit der  -Achse bildet.
-Achse bildet.
1 Abszissen ermitteln
Wir denken daran, dass die Steigung einer Geraden gleich dem Tangens des Winkels ist, den sie mit der  -Achse bildet.
-Achse bildet.
Das heißt 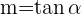
Die Ableitung von  gibt uns die Steigung der Tangente an
gibt uns die Steigung der Tangente an

Da die Tangente einen Winkel von 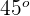 mit der
mit der  -Achse bilden soll, muss die Steigung
-Achse bilden soll, muss die Steigung  betragen.
betragen.
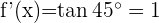
Somit
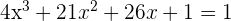
Wir bestimmen
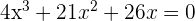
Wir klammern ein x aus

Eine Lösung ist

Die anderen Lösungen erhalten wir durch

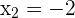

2 Ordinaten ermitteln
Wir überprüfen die Punkte in der usprünglichen Funktion 
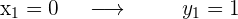
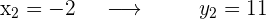
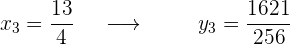
Zum Schluss
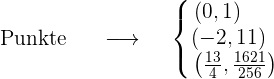
An welchem Punkt der Kurve  ist die Tangente parallel zur Sehne, die die Punkte (1, 0) und (e, 1) verbindet?
ist die Tangente parallel zur Sehne, die die Punkte (1, 0) und (e, 1) verbindet?
Die Steigung der Sehne muss gleich der Ableitung der Funktion sein.
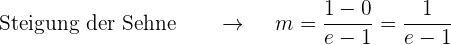
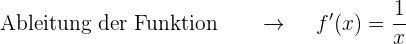
Somit

Wir setzen diesen Punkt in  ein, um die Ordinate zu ermitteln zu können
ein, um die Ordinate zu ermitteln zu können
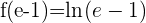
Zum Schluss
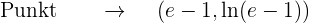
Berechne die Gleichung der Geraden
Berechne die Gleichung der Tangente und der Normalen der Kurve 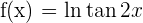 im Punkt auf der x-Achse:
im Punkt auf der x-Achse: 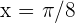 .
.
1
Die Steigung ermitteln
Wir leiten die Funktion ab, da uns die Ableitung die Steigung der Tangente angibt
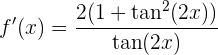
Wir rechnen mit 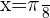
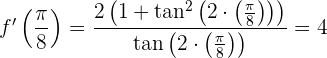
Die Koordinaten des Berührungspunktes ermitteln
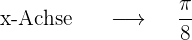
Wie werten die ursprüngliche Funktion an diesem Punkt 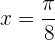 aus, um die y-Achse zu erhalten
aus, um die y-Achse zu erhalten
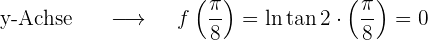
Die Gleichung der Tangente ermitteln
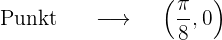
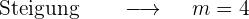
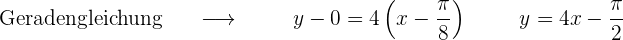
2 Normale
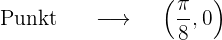
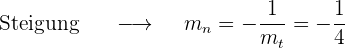
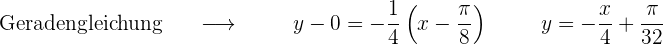
Gegeben ist die Gleichung  . Bestimme die Gleichung der Tangente, die parallel zur Geraden mit der Gleichung
. Bestimme die Gleichung der Tangente, die parallel zur Geraden mit der Gleichung  ist.
ist.
Die Gleichung  , wenn wir nach
, wenn wir nach  auflösen, kann auch wie folgt geschrieben werden
auflösen, kann auch wie folgt geschrieben werden

Durch implizite Ableitung der Gleichung erhalten wir:
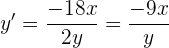
Und da uns die Ableitung die Steigung der Tangente angibt, setzen wir gleich 3

Wir erhalten ein Gleichungssystem mit 2x2
Wir lösen, indem wir die zweite Gleichung in die erste Gleichung einsetzen
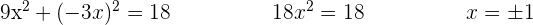
Um die Ordinate der Punkte zu erhalten, setzt man einfach den Wert von  in die einfachste Gleichung des Systems ein
in die einfachste Gleichung des Systems ein


Wir erhalten die Gleichung der Geraden an diesen Punkten
1 x=1
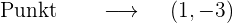
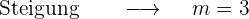
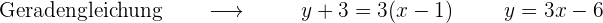
2 x=-1
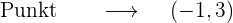
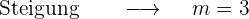
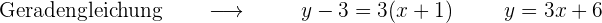
Bestimme die Parameter
Bestimme die Werte des Parameters b, sodass die Tangenten an der Funktionskurve  an den Punkten auf der x-Achse
an den Punkten auf der x-Achse  ,
,  parallel sind.
parallel sind.
Die Ableitung von  ist
ist

Damit sie parallel sind, müssen die Ableitungen bei  und
und  gleich sein. Das heißt
gleich sein. Das heißt

Also
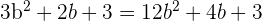

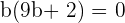
Eine Lösung ist

Die andere Lösung ist

Ermittle die Koeffizienten der Gleichung  , wobei du weißt, dass ihr Graph durch
, wobei du weißt, dass ihr Graph durch  und
und  verläuft und die Steigung der Tangente an diesem letzten Punkt
verläuft und die Steigung der Tangente an diesem letzten Punkt  ist.
ist.
Wir erhalten  Gleichungen, wenn wir den Wert der Abszisse in
Gleichungen, wenn wir den Wert der Abszisse in  einsetzen und gleich dem Wert der Ordinate der Punkte, die durch den Graphen gehen, setzen
einsetzen und gleich dem Wert der Ordinate der Punkte, die durch den Graphen gehen, setzen
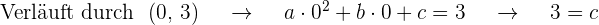
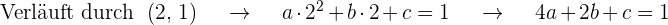
Außerdem ist die Steigung der Tangente gegeben durch

Wenn die Steigung im Punkt  3 ist, bedeutet das
3 ist, bedeutet das

Wir lösen das Gleichungssystem (3x3) und erhalten:
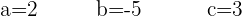
Die Gleichung lautet wie folgt
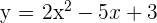
Der Graph der Funktion  verläuft durch die Punkte
verläuft durch die Punkte  und
und 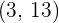 , wobei die Tangente am Punkt
, wobei die Tangente am Punkt  auf der x-Achse parallel zur Winkelhalbierenden des 1. Quadranten ist. Bestimme den numerischen Wert von
auf der x-Achse parallel zur Winkelhalbierenden des 1. Quadranten ist. Bestimme den numerischen Wert von  und
und  .
.
Wir erhalten  Gleichungen, wenn wir die Werte der x-Achse
Gleichungen, wenn wir die Werte der x-Achse  einsetzen und gleich dem Wert der Ordinate der Punkte, die durch den Graphen gehen, gleichsetzen
einsetzen und gleich dem Wert der Ordinate der Punkte, die durch den Graphen gehen, gleichsetzen
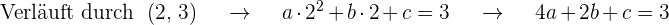
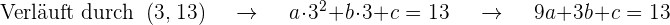
Außerdem ist die Steigung der Tangente gegeben durch

Wenn die Steigung im Punkt  parallel zur Winkelhalbierenden ist, bedeutet das für die Steigung
parallel zur Winkelhalbierenden ist, bedeutet das für die Steigung 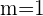
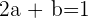
Wir lösen das Gleichungssystem und erhalten:
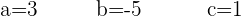
Die Gleichung lautet wie folgt
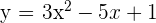
Gegeben ist die Funktion 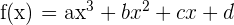 . Bestimme
. Bestimme  und
und  ; die Kurve verläuft dabei durch die Punkte
; die Kurve verläuft dabei durch die Punkte  . Außerdem sind die Tangenten an den Punkten der x-Achse
. Außerdem sind die Tangenten an den Punkten der x-Achse  und
und  parallel zur
parallel zur  -Achse.
-Achse.
Wir erhalten  Gleichungen, wenn wir den Wert der Abszisse in
Gleichungen, wenn wir den Wert der Abszisse in  einsetzen und ihn mit dem Wert der Ordinate der durch den Graphen verlaufenden Punkte gleichsetzen.
einsetzen und ihn mit dem Wert der Ordinate der durch den Graphen verlaufenden Punkte gleichsetzen.
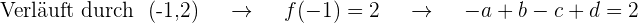
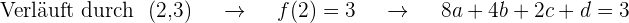
Außerdem ist die Steigung der Tangente gegeben durch

Wenn die Steigung am Punkt  parallel zur Winkelhalbierenden des Quadranten ist, bedeutet das für die Steigung
parallel zur Winkelhalbierenden des Quadranten ist, bedeutet das für die Steigung 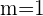


Wir lösen das System (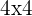 ) und erhalten:
) und erhalten:
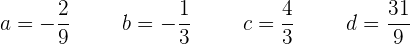
Wir erhalten folgende Gleichung
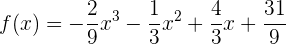
Bestimme den Winkel oder die Fläche
Gegeben ist die Funktion 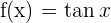 . Bestimme den Winkel, den die Tangente am Graphen der Funktion
. Bestimme den Winkel, den die Tangente am Graphen der Funktion  im Ursprung mit der x-Achse bildet.
im Ursprung mit der x-Achse bildet.
Die Tangente hat die Steigung

Im Ursprung ist diese Steigung

Wir denken daran, dass die Steigung einer Geraden gleich dem Tangens des Winkels ist, den sie mit der Achse  bildet.
bildet.
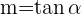
Somit
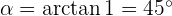
Bestimme die Fläche des Dreiecks, das durch die Koordinatenachsen und die Tangente an der Kurve 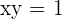 am Punkt
am Punkt  bestimmt wird.
bestimmt wird.
Wenn 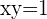 , ist
, ist 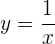
Die Steigung der Tangente ist gegeben durch die Ableitung
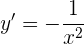
Wir ermitteln die Steigung bei 
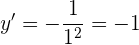
Die Ordinate erhalten wir anhand der usprünglichen Funktion
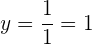
Zum Schluss
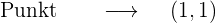
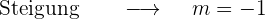
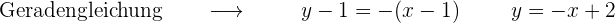
Schnittpunkt mit der Achse OX

Ein Schnittpunkt ist 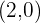
Schnittpunkt OY
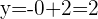
Der andere Schnittpunkt ist 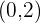
Und so sieht die Abbildung aus
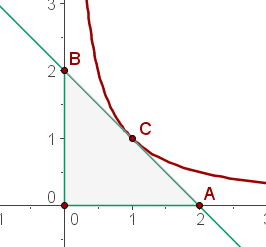
Da das Dreieck rechtwinklig ist, sind seine Basis und Höhe durch die Katheten gegeben. Diese messen in diesem Fall jeweils  . Die Fläche ist
. Die Fläche ist

Mit KI zusammenfassen:












