In diesem Artikel geht es um bestimmte Merkmale trigonometrischer Funktionen, wie ihre Graphen, ihre Definitionsbereiche, Kontinuität usw.

Sinus
Begonnen wird mit der Sinusfunktion

diese Funktion hat den folgenden Graphen:

Beachte, dass diese Funktion für alle reellen Zahlen wohldefiniert ist, ihr Bereich ist also die reellen Zahlen  . Dies bedeutet, dass
. Dies bedeutet, dass

Die Bildmenge (oder einfach Bild oder Pfad) einer Funktion ist die Menge der Werte, die die Funktion annimmt, nachdem sie auf alle Elemente des Bereichs angewendet wurde. In diesem Fall ist es klar, dass die Bildmenge das geschlossene Intervall  ist, also
ist, also

Eine weitere wichtige Eigenschaft der Sinusfunktion ist, dass sie periodisch ist, d. h. es gibt eine reelle Zahl  , für die gilt
, für die gilt

in diesem Fall ist die Periode  im Bogenmaß.
im Bogenmaß.
Aus dem Graphen ist auch ersichtlich, dass die Funktion für alle  stetig ist, denn egal, von wo aus man sich einem Punkt des Graphen nähert, ob von links oder von rechts, man kommt immer an denselben Punkt
stetig ist, denn egal, von wo aus man sich einem Punkt des Graphen nähert, ob von links oder von rechts, man kommt immer an denselben Punkt
Schließlich ist zu beachten, dass die Funktion ungerade ist, d. h. für alle  gilt
gilt

Zusammenfassend lässt sich also Folgendes feststellen:
1 Bereich:  .
.
2 Bildmenge:  .
.
3 Periode:  .
.
4 Stetig: In seinem gesamten Bereich  .
.
5 Ungerade Funktion
Kosinus
Jetzt geht es weiter mit der Kosinusfunktion

diese Funktion hat den folgenden Graphen:

Beachte, dass diese Funktion für alle reellen Zahlen wohldefiniert ist, ihr Bereich ist also die reellen Zahlen  . Dies bedeutet, dass
. Dies bedeutet, dass

Die Bildmenge (oder einfach Bild oder Pfad) einer Funktion ist die Menge der Werte, die die Funktion annimmt, nachdem sie auf alle Elemente des Bereichs angewendet wurde. In diesem Fall ist es klar, dass das Bild das geschlossene Intervall  ist, also
ist, also

Eine weitere wichtige Eigenschaft der Kosinusfunktion ist, dass sie periodisch ist, d. h. es gibt eine reelle Zahl  , für die gilt
, für die gilt

in diesem Fall ist die Periode  im Bogenmaß.
im Bogenmaß.
Aus dem Graphen ist auch ersichtlich, dass die Funktion für alle  stetig ist, denn egal, von wo aus man sich einem Punkt des Graphen nähert, ob von links oder von rechts, man kommt immer an denselben Punkt.
stetig ist, denn egal, von wo aus man sich einem Punkt des Graphen nähert, ob von links oder von rechts, man kommt immer an denselben Punkt.
Schließlich ist zu beachten, dass die Funktion geradzahlig ist, d. h. für alle  ist erfüllt, dass
ist erfüllt, dass

Zusammenfassend lässt sich also Folgendes feststellen:
1 Bereich:  .
.
2 Bildmenge:  .
.
3 Periode:  .
.
4 Stetig: In seinem gesamten Bereich  .
.
5 Gerade Funktion
Tangens
Zuletzt gibt es die Tangensfunktion

diese Funktion hat den folgenden Graphen:

Beachte, dass diese Funktion für fast jede reelle Zahl gut definiert ist. Hier erfährst Du, warum sie nicht für jede reelle Zahl definiert ist. Die Tangensfunktion ist wie folgt definiert.

Da die Division durch Null undefiniert ist, ist die Tangensfunktion undefiniert, sobald  ist, und das geschieht für alle
ist, und das geschieht für alle  der Form
der Form
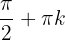 wobei
wobei  ganz ist. Der Tangensbereich ist also
ganz ist. Der Tangensbereich ist also
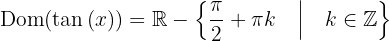
Die Bildmenge (oder einfach Bild oder Pfad) einer Funktion ist die Menge der Werte, die die Funktion annimmt, nachdem sie auf alle Elemente des Bereichs angewendet wurde. In diesem Fall, wenn wir das Bild betrachten, ist es klar, dass die Bildmenge die ganze Menge der Realen ist, d.h.  , also
, also

Eine weitere wichtige Eigenschaft der Tangensfunktion ist, dass sie periodisch ist, d. h. es gibt eine reelle Zahl  , für die gilt
, für die gilt

in diesem Fall ist die Periode  Bogenmaß.
Bogenmaß.
Aus dem Graphen ist auch ersichtlich, dass die Funktion für alle  stetig ist, denn egal, wo Du Dich einem Punkt auf dem Graphen näherst, ob von links oder von rechts, Du kommst immer an denselben Punkt.
stetig ist, denn egal, wo Du Dich einem Punkt auf dem Graphen näherst, ob von links oder von rechts, Du kommst immer an denselben Punkt.
Schließlich ist zu beachten, dass die Funktion ungerade ist, d. h. für alle  ist erfüllt, dass
ist erfüllt, dass

Zusammenfassend lässt sich also Folgendes feststellen:
1 Bereich: 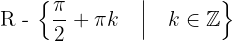 .
.
2 Bildmenge:  .
.
3 Periode:  .
.
4 Stetig: In seinem gesamten Bereich, aber nicht in allen  .
.
5 Ungerade Funktion
Kosekans
Betrachte nun die Funktion des Kosekans

diese Funktion hat den folgenden Graphen:
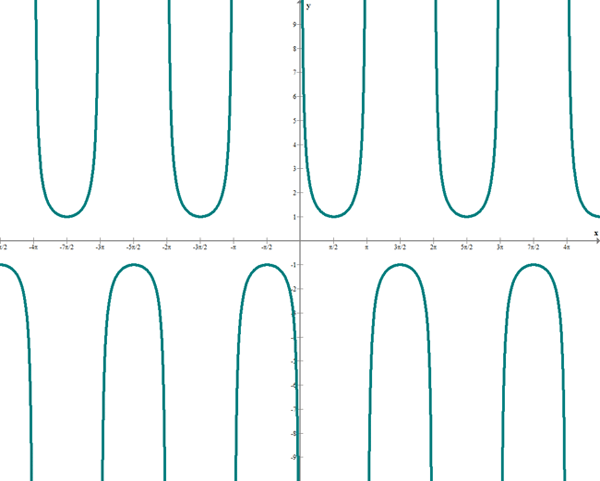
Beachte, dass diese Funktion für alle reellen Zahlen wohldefiniert ist. Um zu verstehen, warum sie nicht für alle  definiert ist, sei daran erinnert, dass die Kosekansfunktion der Kehrwert der Sinusfunktion ist, d. h.
definiert ist, sei daran erinnert, dass die Kosekansfunktion der Kehrwert der Sinusfunktion ist, d. h.

Da die Division durch Null nicht wohldefiniert ist, ist die Kosekans für Werte von  , bei denen der Sinus gleich Null ist, nicht definiert; diese Werte sind
, bei denen der Sinus gleich Null ist, nicht definiert; diese Werte sind  , wobei
, wobei  eine ganze Zahl ist. Daher ist der Bereich der Kosekans
eine ganze Zahl ist. Daher ist der Bereich der Kosekans

Die Bildmenge (oder einfach Bild oder Pfad) einer Funktion ist die Menge der Werte, die die Funktion annimmt, nachdem sie auf alle Elemente des Bereichs angewendet wurde. In diesem Fall erinnern wir uns zunächst daran, dass das Bild des Sinus  . ist. Du betrachtest im Folgenden zwei Fälle: zum einen, wenn sich das Sinusbild in
. ist. Du betrachtest im Folgenden zwei Fälle: zum einen, wenn sich das Sinusbild in  befindet, und zum anderen, wenn sich das Sinusbild in
befindet, und zum anderen, wenn sich das Sinusbild in  befindet.
befindet.
Beginnst Du mit  , so ist klar, dass
, so ist klar, dass

Mit  ist es nun klar, dass
ist es nun klar, dass

Das Bild der Kosekans ist also die Vereinigung der Bilder dieser beiden Fälle

Eine weitere wichtige Eigenschaft der Kosekansfunktion ist, dass sie periodisch ist, d. h. es gibt eine reelle Zahl  , für die gilt
, für die gilt

in diesem Fall ist die Periode  Bogenmaß.
Bogenmaß.
Aus dem Graphen ist auch ersichtlich, dass die Funktion für alle  stetig ist, denn egal, wo Du Dich einem Punkt auf dem Graphen näherst, ob von links oder von rechts, Du kommst immer an denselben Punkt.
stetig ist, denn egal, wo Du Dich einem Punkt auf dem Graphen näherst, ob von links oder von rechts, Du kommst immer an denselben Punkt.
Schließlich ist zu beachten, dass die Funktion ungerade ist, d. h. für alle  ist erfüllt, dass
ist erfüllt, dass

Zusammenfassend lässt sich also Folgendes feststellen:
1 Bereich:  .
.
2 Bildmenge:  .
.
3 Periode:  .
.
4 Stetig: In seinem gesamten Bereich, aber nicht in  .
.
5 Ungerade Funktion
Sekans
Betrachte nun die Sekansfunktion

diese Funktion hat den folgenden Graphen:
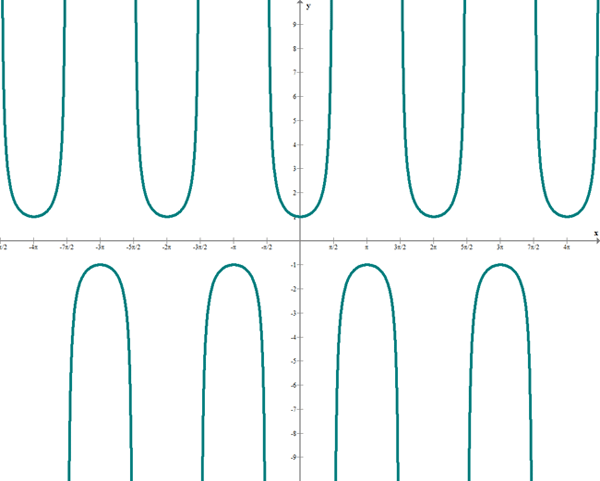
Du stellst fest, dass diese Funktion für alle reellen Zahlen wohldefiniert ist. Um zu verstehen, warum sie nicht für alle  definiert ist, sei daran erinnert, dass die Sekansfunktion der Kehrwert der Kosinusfunktion ist, d. h.
definiert ist, sei daran erinnert, dass die Sekansfunktion der Kehrwert der Kosinusfunktion ist, d. h.

Da die Division durch Null nicht wohldefiniert ist, ist die Sekans für Werte von  , bei denen der Kosinus Null ist, nicht definiert; diese Werte sind
, bei denen der Kosinus Null ist, nicht definiert; diese Werte sind 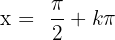 , wobei
, wobei  eine ganze Zahl ist. Daher ist der Bereich des Sekans
eine ganze Zahl ist. Daher ist der Bereich des Sekans
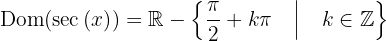
Die Bildmenge (oder einfach Bild oder Pfad) einer Funktion ist die Menge der Werte, die die Funktion annimmt, nachdem sie auf alle Elemente des Bereichs angewendet wurde. In diesem Fall solltest Du Dich zunächst daran erinnern, dass das Kosinusbild  ist. Du wirst nun zwei Fälle betrachten: zum einen, wenn das Kosinusbild bei
ist. Du wirst nun zwei Fälle betrachten: zum einen, wenn das Kosinusbild bei  liegt, und zum anderen, wenn das Kosinusbild bei
liegt, und zum anderen, wenn das Kosinusbild bei  liegt.
liegt.
Beginnst Du mit  , so ist klar, dass
, so ist klar, dass

Mit  ist es nun klar, dass
ist es nun klar, dass

Daher ist das Bild des Sekans die Vereinigung der Bilder dieser beiden Fälle

Eine weitere wichtige Eigenschaft der Sekansfunktion ist, dass sie periodisch ist, d. h. es gibt eine reelle Zahl  , für die gilt
, für die gilt

in diesem Fall ist die Periode  im Bogenmaß.
im Bogenmaß.
Aus dem Graphen ist auch ersichtlich, dass die Funktion für alle  stetig ist, denn egal, wo Du Dich einem Punkt auf dem Graphen näherst, ob von links oder von rechts, Du kommst immer an denselben Punkt.
stetig ist, denn egal, wo Du Dich einem Punkt auf dem Graphen näherst, ob von links oder von rechts, Du kommst immer an denselben Punkt.
Schließlich ist zu beachten, dass die Funktion gerade ist, d. h. für alle  ist erfüllt, dass
ist erfüllt, dass

Zusammenfassend lässt sich also Folgendes feststellen:
1 Bereich: 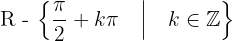 .
.
2 Bildmenge:  .
.
3 Periode:  .
.
4 Stetig: In seinem gesamten Bereich, aber nicht in  .
.
5 Gerade Funktion
Kotangens
Betrachte nun die Kotangensfunktion

diese Funktion hat den folgenden Graphen:
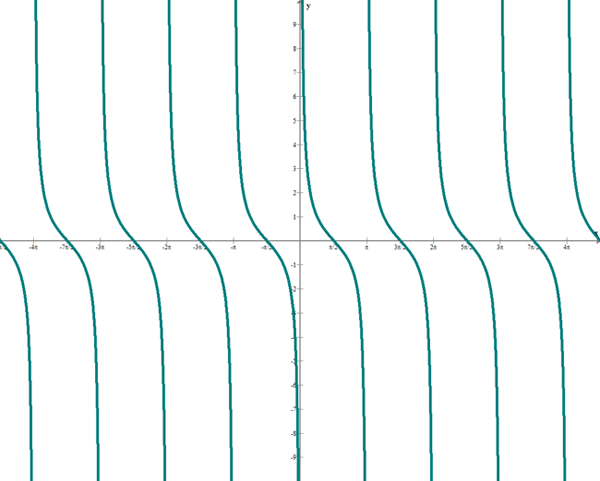
Beachte, dass diese Funktion für alle reellen Zahlen wohldefiniert ist. Um zu verstehen, warum sie nicht über alle  definiert ist, sei daran erinnert, dass die Kotangensfunktion definiert ist als
definiert ist, sei daran erinnert, dass die Kotangensfunktion definiert ist als

Da die Division durch Null nicht gut definiert ist, ist der Kotangens für Werte von  bei denen der Sinus gleich Null ist, nicht definiert; diese Werte sind
bei denen der Sinus gleich Null ist, nicht definiert; diese Werte sind  , wobei
, wobei  eine ganze Zahl ist. Daher ist der Kotangensbereich
eine ganze Zahl ist. Daher ist der Kotangensbereich

Die Bildmenge (oder einfach Bild oder Pfad) einer Funktion ist die Menge der Werte, die die Funktion annimmt, nachdem sie auf alle Elemente des Bereichs angewendet wurde. In diesem Fall ist es klar, dass das Bild wie bei der Tangente alle reellen Zahlen sind, d. h.

Ein weiteres wichtiges Merkmal der Kotangensfunktion ist, dass sie periodisch ist, d. h. es gibt eine reelle Zahl  , für die gilt
, für die gilt

in diesem Fall ist die Periode  Bogenmaß.
Bogenmaß.
Aus dem Graphen ist auch ersichtlich, dass die Funktion für alle  stetig ist, denn egal, wo Du Dich einem Punkt auf dem Graphen näherst, ob von links oder von rechts, Du kommst immer an denselben Punkt.
stetig ist, denn egal, wo Du Dich einem Punkt auf dem Graphen näherst, ob von links oder von rechts, Du kommst immer an denselben Punkt.
Schließlich ist zu beachten, dass die Funktion ungerade ist, d. h. für alle  ist erfüllt, dass
ist erfüllt, dass

Zusammenfassend lässt sich also Folgendes feststellen:
1 Bereich:  .
.
2 Bildmenge:  .
.
3 Periode:  .
.
4 Stetig: In seinem gesamten Bereich, aber nicht in  .
.
5 Ungerade Funktion
Mit KI zusammenfassen:













