Bestimme die Koordinaten des Mittelpunkts sowie den Radius der folgenden Kreise

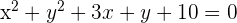
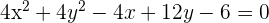

Wir denken daran, dass, wenn die Gleichung eines Kreises gegeben ist durch
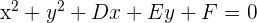 ,
,
der Mittelpunkt  des Kreises die Koordinaten
des Kreises die Koordinaten
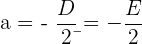
hat und der Radius  folgende Gleichung erfüllt
folgende Gleichung erfüllt
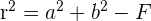
Mit diesem Wissen können wir folgende Aufgaben lösen:

Zunächst bestimmen wir den Mittelpunkt  des Kreises
des Kreises
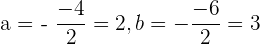
Der Mittelpunkt ist somit 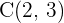 .
.
Außerdem muss der Radius  folgende Bedingung erfüllen
folgende Bedingung erfüllen
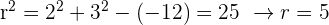
Somit ist der Radius 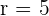 .
.
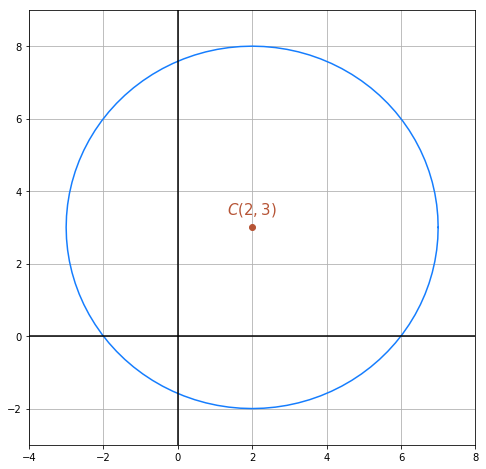
Die folgende Abbildung zeigt den Kreis graphisch dargestellt:
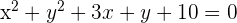
Zunächst bestimmen wir den Mittelpunkt 
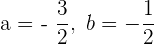
Somit befindet sich der Mittelpunkt im Punkt 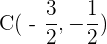 .
.
Außerdem muss der Radius  folgende Bedingung erfüllen
folgende Bedingung erfüllen
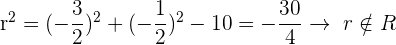
Daher haben wir keinen wirklichen Kreis.
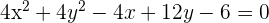
Bevor wir den Mittelpunkt und den Radius berechnen, müssen wir durch 4 dividieren. Die Gleichung hat somit die Form, mit der wir bereits umgehen können.
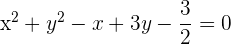
Nun bestimmen wir den Mittelpunkt  des Kreises:
des Kreises:
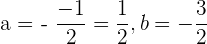
Der Mittelpunkt befindet sich also im Punkt 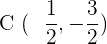 .
.
Andererseits muss der Radius  folgende Bedingung erfüllen
folgende Bedingung erfüllen
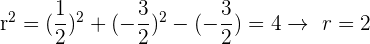
Somit ist der Radius  . Die folgende Abbildung zeigt den Kreis graphisch dargestellt:
. Die folgende Abbildung zeigt den Kreis graphisch dargestellt:
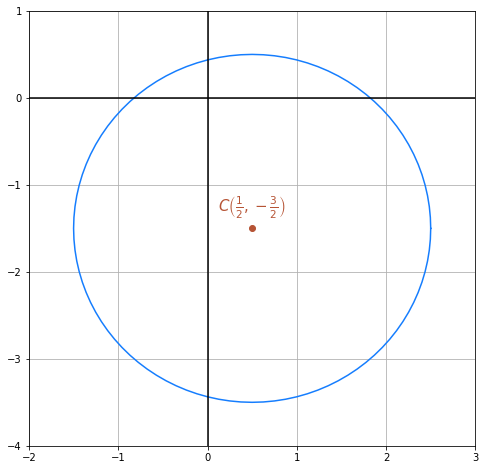

Wie in der vorherigen Aufgabe müssen wir vor der Berechnung des Mittelpunkts und des Radius durch 4 dividieren
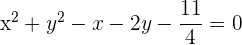
Nun bestimmen wir den Mittelpunkt des Kreises:
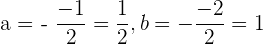
Somit befindet sich der Mittelpunkt bei 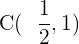 .
.
Andererseits muss der Radius  folgende Bedingung erfüllen
folgende Bedingung erfüllen
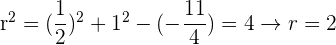
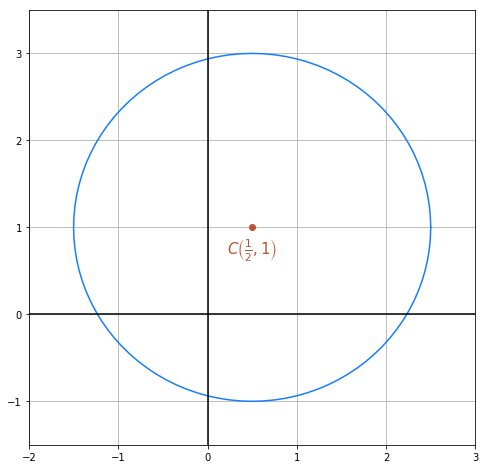
Somit ist der Radius  . Graphisch dargestellt sieht der Kreis wie folgt aus:
. Graphisch dargestellt sieht der Kreis wie folgt aus:
Bestimme die Gleichung des Kreises, der seinen Mittelpunkt bei hat und der die x-Achse tangiert.
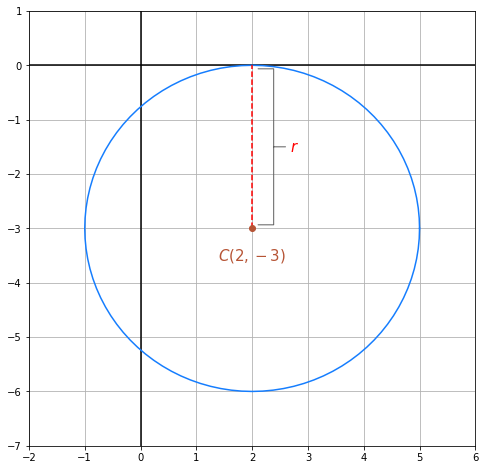
Bestimme die Gleichung des Kreises, der seinen Mittelpunkt bei (2, -3) hat und der die x-Achse tangiert.
Graphisch dargestellt muss der Kreis wie folgt aussehen:
Wir wissen bereits, dass der Mittelpunkt bei 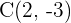 liegt. Außerdem ist die x-Achse die Gerade
liegt. Außerdem ist die x-Achse die Gerade 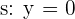 . Somit ist die Entfernung zwischen dem Punkt
. Somit ist die Entfernung zwischen dem Punkt  und der Geraden
und der Geraden  gegeben durch
gegeben durch
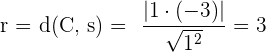
Daher muss der Radius des Kreises 3 sein. Die Kreisgleichung lautet also:
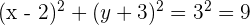
Bestimme die Gleichung des Kreises, dessen Mittelpunkt bei liegt und der die x-Achse tangiert.
Bestimme die Gleichung des Kreises, dessen Mittelpunkt bei (-1, 4) liegt und der die y-Achse tangiert.
Die graphische Darstellung sieht wie folgt aus:
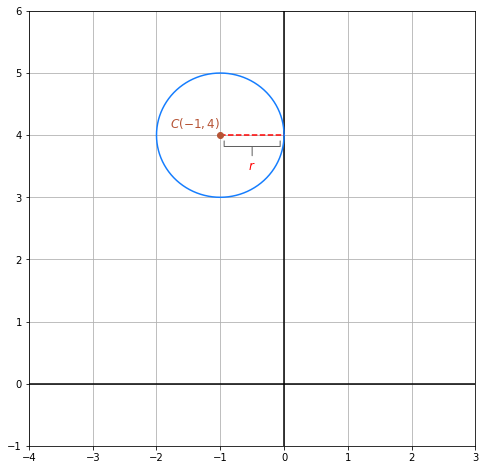
Dieses Problem wird auf ganz ähnliche Weise wie in der vorherigen Aufgabe gelöst. Wir wissen, dass der Mittelpunkt bei  liegt. Außerdem ist die y-Achse die Gerade
liegt. Außerdem ist die y-Achse die Gerade 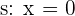 . Somit ist die Entfernung zwischen Punkt
. Somit ist die Entfernung zwischen Punkt  und der Geraden
und der Geraden  gegeben durch
gegeben durch
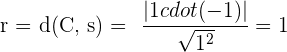
Deshalb muss der Radius des Kreises 1 sein. Somit lautet die Gleichung des Kreises wie folgt:
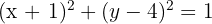
Bestimme die Gleichung des Kreises, dessen Mittelpunkt im Schnittpunkt der Geraden 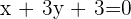 und
und 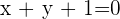 liegt und dessen Radius
liegt und dessen Radius  ist.
ist.
Wir haben folgende Geraden, deren Schnittpunkt der Punkt  ist. Wir möchten die Gleichung des folgenden Kreises (blau) bestimmen:
ist. Wir möchten die Gleichung des folgenden Kreises (blau) bestimmen:
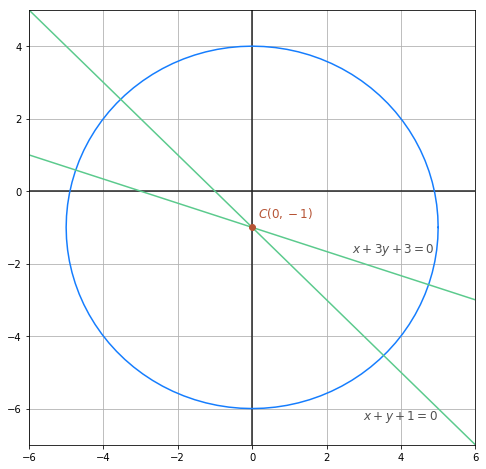
Wir müssen den Schnittpunkt der beiden Geraden finden. Das bedeutet, dass wir das folgende Gleichungssystem lösen müssen:
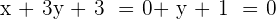
Die Lösungen des Systems aus den Gleichungen sind  und
und  . Deshalb muss der Mittelpunkt des Kreises bei
. Deshalb muss der Mittelpunkt des Kreises bei  liegen. Somit lautet die Gleichung des Kreises wie folgt
liegen. Somit lautet die Gleichung des Kreises wie folgt
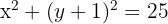
Bestimme die Gleichung des Kreises, der konzentrisch zum Kreis mit der Gleichung  ist und durch den Punkt (-3, 4) verläuft.
ist und durch den Punkt (-3, 4) verläuft.
Wir sehen uns folgende Abbildung an:
https://www.superprof.es/apuntes/wp-content/uploads/2019/06/ejercicio-circunferencia2-5.png
Wir suchen die Gleichung des blauen Kreises (er hat denselben Mittelpunkt wie der grüne Kreis und verläuft durch den roten Punkt).
Da die Kreise konzentrisch sind, haben sie denselben Mittelpunkt. Deshalb müssen wir den Mittelpunkt des anderen Kreises bestimmen:
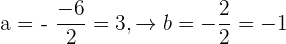
Somit ist der Mittelpunkt der Punkt  . Außerdem muss der Kreis durch den Punkt
. Außerdem muss der Kreis durch den Punkt  verlaufen. Das heißt, dass der Radius
verlaufen. Das heißt, dass der Radius  des Kreises die Distanz zwischen diesen beiden Punkten ist:
des Kreises die Distanz zwischen diesen beiden Punkten ist:

Somit lautet die Gleichung des Kreises wie folgt

Bestimme die Gleichung des Umkreises des Dreiecks mit den Scheitelpunkten: A (0,0), B(3, 1), C (5, 7)
Der Umkreis muss durch jeden der Punkte verlaufen. Dies bedeutet: Wenn die Werte für  und
und  in die Gleichung des Kreises
in die Gleichung des Kreises 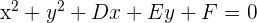 eingesetzt werden, muss dies null ergeben. Deshalb ergibt sich folgendes System:
eingesetzt werden, muss dies null ergeben. Deshalb ergibt sich folgendes System:
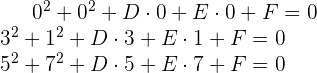
Das vorhergehende System ist äquivalent zu folgendem Gleichungssystem, nachdem die Konstanten, die nicht mit  ,
,  oder
oder  multipliziert werden, auf der rechten Seite jeder Gleichung bestimmt wurden:
multipliziert werden, auf der rechten Seite jeder Gleichung bestimmt wurden:
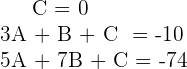
Dieses System hat folgende Lösung:
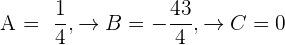
Deshalb ist die Gleichung des Umkreises
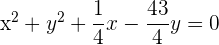
Wir sehen uns die graphische Darstellung des Kreises an:
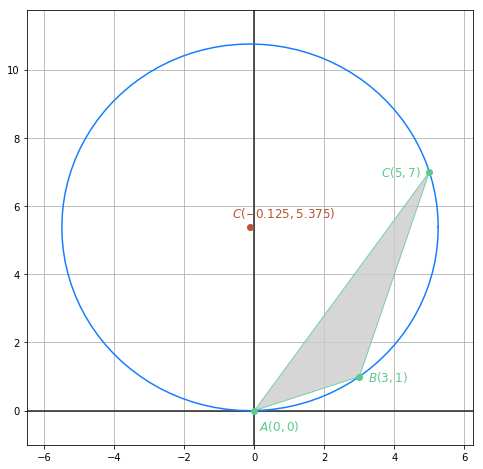
Die äußersten Punkte des Durchmessers eines Kreises sind die Punkte A (-5, 3) und B (3, 1). Wie lautet die Gleichung dieses Kreises?
Wir sehen uns die folgende graphische Darstellung an:
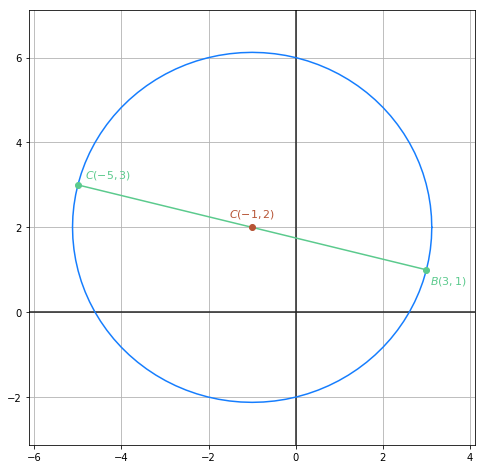
Die äußersten Punkte des Durchmessers des Kreises sind die Punkte  und
und  . Deshalb muss der Radius
. Deshalb muss der Radius  die Hälfte des Abstands zwischen
die Hälfte des Abstands zwischen  und
und  sein. Das heisst,
sein. Das heisst,
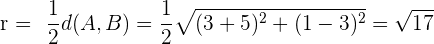
Außerdem befindet sich der Mittelpunkt in der Mitte von  und
und  . Dies ist gegeben durch
. Dies ist gegeben durch
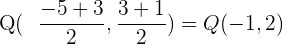
Somit ist die Gleichung des Kreises gegeben durch:
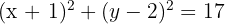
Bestimme die Gleichung des konzentrischen Kreises zum Kreis  , der die Gerade
, der die Gerade  tangiert.
tangiert.
Um diese Aufgabe zu lösen, müssen wir zunächst den Mittelpunkt des Kreises bestimmen (der mit dem des anderen gegebenen Kreises identisch ist). Danach müssen wir die Distanz zur gegebenen Geraden bestimmen: Diese Distanz ist dann der Radius unseres Kreises.
Somit ist der Mittelpunkt des Kreises
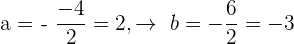
Der Mittelpunkt befindet sich also im Punkt 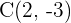 . Der Radius ist
. Der Radius ist
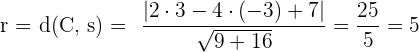
Folglich ist die Kreisgleichung gegeben durch
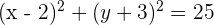
Die graphische Darstellung sieht wie folgt aus:
Bestimme die relative Lage des Kreises 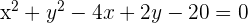 in Bezug auf folgende Geraden:
in Bezug auf folgende Geraden:
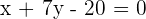

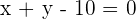
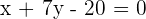
Um die relative Lage zwischen der Geraden und des Kreises zu bestimmen, müssen wir die Punkte finden, in denen sie sich schneiden. Das heißt, wir müssen das folgende nichtlineare Gleichungssystem lösen:
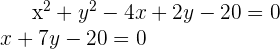
Aus der zweiten Gleichung erhalten wir  . Indem wir in die erste Gleichung einsetzen, erhalten wir (nachdem wir vereinfacht haben):
. Indem wir in die erste Gleichung einsetzen, erhalten wir (nachdem wir vereinfacht haben):
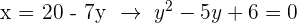
Die Lösungen der quadratischen Gleichung sind  und
und 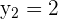 , die wir mithilfe der quadratischen Formel ermittelt haben. Indem wir in das zweite nichtlineare Gleichungssystem einsetzen, erhalten wir:
, die wir mithilfe der quadratischen Formel ermittelt haben. Indem wir in das zweite nichtlineare Gleichungssystem einsetzen, erhalten wir:
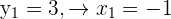
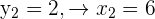
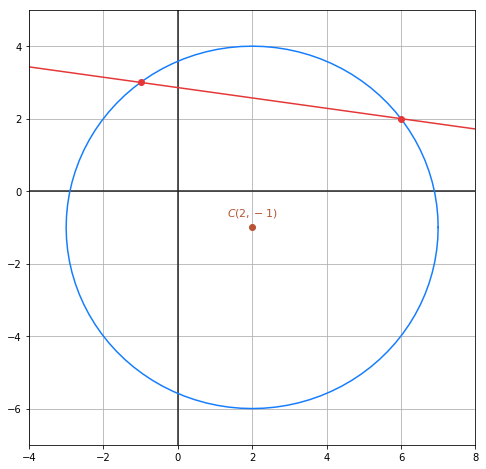
Q (6, 2) und P (-1, 3) sind somit die Schnittpunkte zwischen Gerade und Kreis. Die Gerade ist also eine Sekante des Kreises, wie in der folgenden Grafik zu sehen ist.

Auf die gleiche Weise wie im vorhergehenden Abschnitt müssen wir das folgende nichtlineare Gleichungssystem lösen:
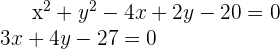
Indem wir  aus der zweiten Gleichung erhalten und es in die erste Gleichung einsetzen, erhalten wir
aus der zweiten Gleichung erhalten und es in die erste Gleichung einsetzen, erhalten wir
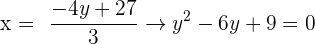
Wir stellen fest, dass die quadratische Gleichung nur eine einzige Lösung hat, nämlich  . Indem wir in die zweite Gleichung einsetzen, erhalten wir
. Indem wir in die zweite Gleichung einsetzen, erhalten wir  .
.
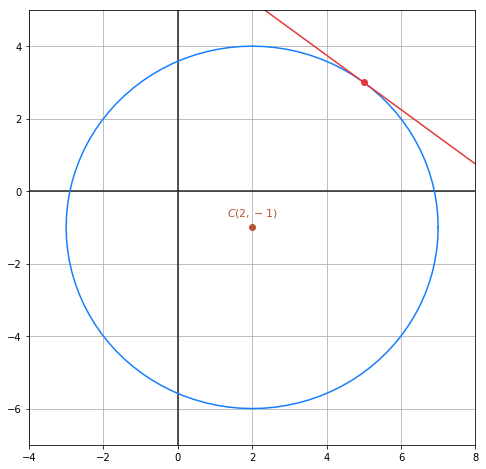
Daher schneidet die Gerade den Kreis nur im Punkt  . Das heißt, die Gerade tangiert den Kreis, wie in der folgenden Abbildung zu sehen ist:
. Das heißt, die Gerade tangiert den Kreis, wie in der folgenden Abbildung zu sehen ist:
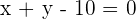
Schließlich wird auch dieses Problem auf die gleiche Weise wie bisher gelöst. Wir sehen uns also das folgende nichtlineare Gleichungssystem an
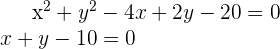
Indem wir  aus der zweiten Gleichung erhalten und in die erste Gleichung einsetzen, erhalten wir
aus der zweiten Gleichung erhalten und in die erste Gleichung einsetzen, erhalten wir
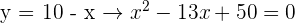
Wir stellen fest, dass die Diskriminante der Gleichung wie folgt lautet:

Daher hat die quadratische Gleichung keine reellen Lösungen. Das heißt, dass das Gleichungssystem keine reellen Lösungen hat.
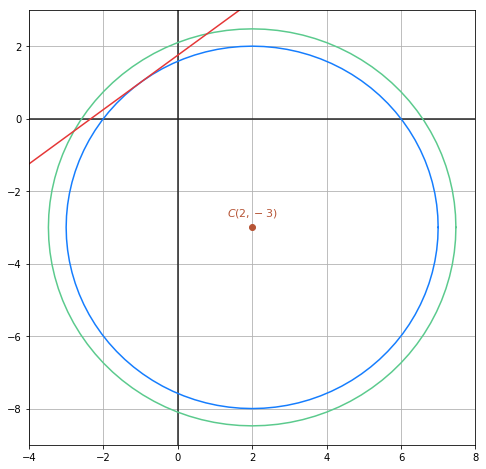
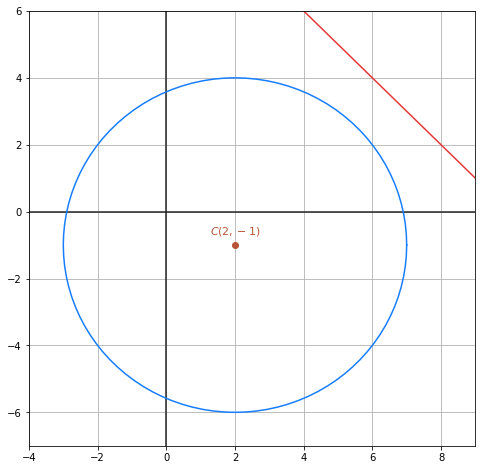
Somit schneidet die Gerade den Kreis an keinem Punkt. Das heißt, die Gerade ist eine Passante, wie in der folgenden Abbildung zu sehen ist:
Mit KI zusammenfassen:



