
Die Elemente der Ellipse bestimmen
Stelle grafisch dar und bestimme die Koordinaten der Brennpunkte, der Schnittpunkte und die Exzentrizität der folgenden Ellipsen.

1 Hauptachse
Die Ellipsengleichung liegt bereits in Normalform vor, sodass wir den Wert der großen Halbachse ermitteln können.

Somit können wir die Scheitelpunkte bestimmen, die die Hauptachse bilden

2 Nebenachse
Somit ist der Wert der kleinen Halbachse

Die Scheitelpunkte, die auf der Nebenachse liegen, sind also

3 Brennpunkte
Zuletzt berechnen wir den Wert der linearen Exzentrizität

Damit können wir die Brennpunkte bestimmen

4 Exzentrizität
Die Exzentrizität ist gleich dem Quotienten der linearen Exzentrizität und der großen Halbachse

5 Grafik
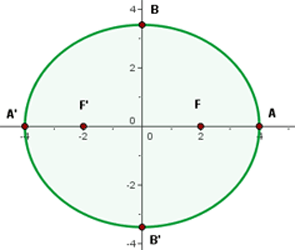

1 Die Normalform erhalten

2 Hauptachse
Wir erhalten den Wert der großen Halbachse

Damit ermitteln wir die Scheitelpunkte, die die Hauptachse bilden

3 Nebenachse
Somit ist der Wert der kleinen Halbachse

Die Scheitelpunkte, die auf der Nebenachse liegen, sind also

4 Brennpunkte
Zuletzt berechnen wir den Wert der linearen Exzentrizität

Damit können wir die Brennpunkte bestimmen

5 Exzentrizität
Die Exzentrizität ist gleich dem Quotienten der linearen Exzentrizität und der großen Halbachse
6 Grafik
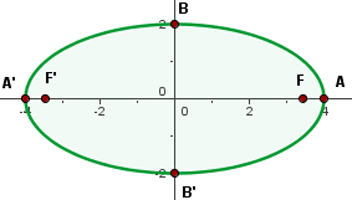
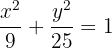
1 Hauptachse
Die Ellipsengleichung liegt bereits in kanonischer Form vor, sodass wir den Wert der großen Halbachse bestimmen können

Damit ermitteln wir die Scheitelpunkte, die die Hauptachse bilden

2 Nebenachse
Somit ist der Wert der kleinen Halbachse

Die Scheitelpunkte, die auf der Nebenachse liegen, sind also

3 Brennpunkte
Zuletzt berechnen wir den Wert der linearen Exzentrizität

Damit können wir die Brennpunkte bestimmen

4 Exzentrizität
Die Exzentrizität ist gleich dem Quotienten der linearen Exzentrizität und der großen Halbachse

5 Grafik
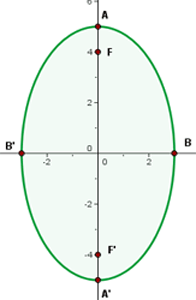
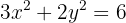
1 Die Normalform erhalten

2 Hauptachse
Die Ellipsengleichung liegt bereits in der Normalform vor, sodass wir den Wert der großen Halbachse bestimmen können

Damit ermitteln wir die Scheitelpunkte, die die Hauptachse bilden

3 Nebenachse
Somit ist der Wert der kleinen Halbachse

Die Scheitelpunkte, die auf der Nebenachse liegen, sind also

4 Brennpunkte
Zuletzt berechnen wir den Wert der linearen Exzentrizität

Damit können wir die Brennpunkte bestimmen

5 Exzentrizität
Die Exzentrizität ist gleich dem Quotienten der linearen Exzentrizität und der großen Halbachse

6 Grafik
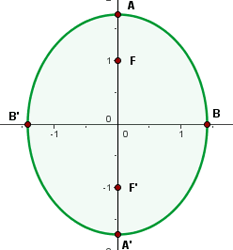
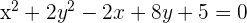
1 Die Normalform erhalten
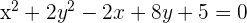
Wir ergänzen das Trinom zum vollständigen Quadrat
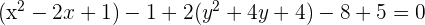
Wir ersetzen die Trinome durch Binome zum Quadrat
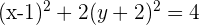
Wir dividieren durch 4
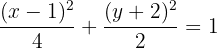
2 Mittelpunkt
Aus der Normalform der Ellipsengleichung ergibt sich der Mittelpunkt
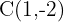
3 Hauptachse
Die Ellipsengleichung liegt bereits in der Normalform vor, sodass wir den Wert der großen Halbachse bestimmen können

Damit ermitteln wir die Scheitelpunkte, die die Hauptachse bilden

4 Nebenachse
Der Wert der kleinen Halbachse ist

Die Scheitelpunkte, die auf der Nebenachse liegen, sind also

5 Brennpunkte
Zuletzt berechnen wir den Wert der linearen Exzentrizität

Damit können wir die Brennpunkte bestimmen

6 Grafik
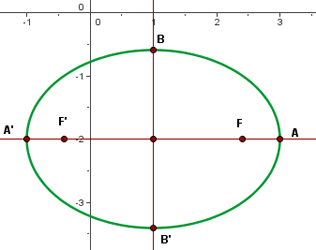
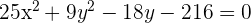
1 Die Normalform erhalten
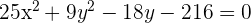
Wir ergänzen das Trinom zum vollständigen Quadrat
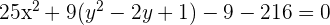
Wir ersetzen die Trinome durch Binome zum Quadrat
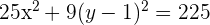
Wir dividieren durch 225
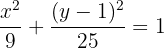
2 Mittelpunkt
Aus der Normalform der Ellipsengleichung ergibt sich der Mittelpunkt
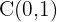
3 Hauptachse
Die Ellipsengleichung liegt bereits in der Normalform vor, sodass wir den Wert der großen Halbachse bestimmen können

Damit ermitteln wir die Scheitelpunkte, die die Hauptachse bilden

4 Nebenachse
Der Wert der kleinen Halbachse ist

Die Scheitelpunkte, die auf der Nebenachse liegen, sind also

5 Brennpunkte
Zuletzt berechnen wir den Wert der linearen Exzentrizität

Damit können wir die Brennpunkte bestimmen

6 Grafik
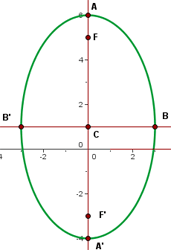
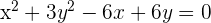
1 Die Normalform erhalten
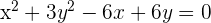
Wir ergänzen das Trinom zum vollständigen Quadrat
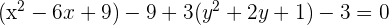
Wir ersetzen die Trinome durch Binome zum Quadrat
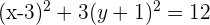
Wir dividieren durch 12
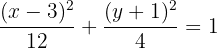
2 Mittelpunkt
Aus der Normalform der Ellipsengleichung ergibt sich der Mittelpunkt
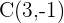
3 Hauptachse
Die Ellipsengleichung liegt bereits in der Normalform vor, sodass wir den Wert der großen Halbachse bestimmen können

Somit bestimmen wir die Scheitelpunkte, die die Hauptachse bilden

4 Nebenachse
Der Wert der kleinen Hauptachse ist

Die Scheitelpunkte, die auf der Nebenachse liegen, sind also

5 Brennpunkte
Zuletzt berechnen wir den Wert der linearen Exzentrizität

Damit können wir die Brennpunkte bestimmen

6 Grafik
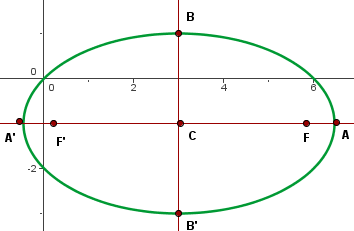
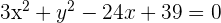
1 Die Normalform erhalten
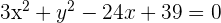
Wir ergänzen das Trinom zu einem vollständigen Quadrat
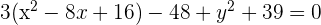
Wir ersetzen die Trinome durch Binome zum Quadrat
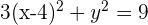
Wir dividieren durch 9
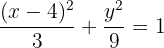
1 Mittelpunkt
Aus der Normalform der Ellipsengleichung ergibt sich der Mittelpunkt

3 Hauptachse
Die Ellipsengleichung liegt bereits in der Normalform vor, sodass wir den Wert der großen Halbachse bestimmen können

Somit können wir die Scheitelpunkte bestimmen, die die Hauptachse bilden

4 Nebenachse
Der Wert der kleinen Halbachse ist

Die Scheitelpunkte, die auf der Nebenachse liegen, sind also

5 Brennpunkte
Zuletzt berechnen wir den Wert der linearen Exzentrizität

Damit können wir die Brennpunkte bestimmen

6 Grafik
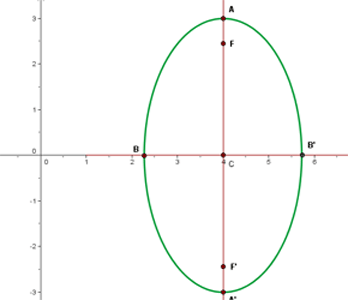
Bestimme die Ellipsengleichung
Bestimme die Ellipsengleichung. Folgende Punkte sind bekannt:
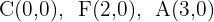

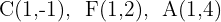
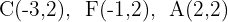
1 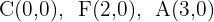
Der Wert für  ist die Distanz vom Mittelpunkt bis zum Scheitelpunkt A. Der Wert für
ist die Distanz vom Mittelpunkt bis zum Scheitelpunkt A. Der Wert für  ist die Distanz zwischen dem Mittelpunkt und dem Brennpunkt. Somit gilt:
ist die Distanz zwischen dem Mittelpunkt und dem Brennpunkt. Somit gilt:

Die Werte  ,
,  und
und  stehen in einem pythagoreischen Verhältnis, das heißt
stehen in einem pythagoreischen Verhältnis, das heißt
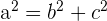
Wir formen entsprechend um, um den Wert für  zu berechnen
zu berechnen


Wir stellen fest, dass
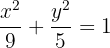
2 
Der Wert für  ist die Distanz zwischen dem Mittelpunkt und dem Scheitelpunkt A. Der Wert für
ist die Distanz zwischen dem Mittelpunkt und dem Scheitelpunkt A. Der Wert für  ist die Distanz zwischen dem Mittelpunkt und dem Brennpunkt. Somit gilt:
ist die Distanz zwischen dem Mittelpunkt und dem Brennpunkt. Somit gilt:

Die Werte  ,
,  und
und  stehen in einem pythagoreischen Verhältnis, das heißt
stehen in einem pythagoreischen Verhältnis, das heißt
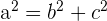
Wir formen entsprechend um, um den Wert für  zu berechnen
zu berechnen

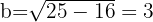
Wir stellen fest, dass
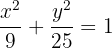
3 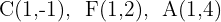
Der Wert für  ist die Distanz zwischen dem Mittelpunkt und dem Scheitelpunkt A. Der Wert für
ist die Distanz zwischen dem Mittelpunkt und dem Scheitelpunkt A. Der Wert für  ist die Distanz zwischen dem Mittelpunkt und dem Brennpunkt. Somit gilt:
ist die Distanz zwischen dem Mittelpunkt und dem Brennpunkt. Somit gilt:

Die Werte  ,
,  und
und  stehen in einem pythagoreischen Verhältnis, das heißt
stehen in einem pythagoreischen Verhältnis, das heißt
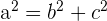
Wir formen entsprechend um, um den Wert für  zu berechnen
zu berechnen

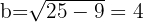
Wir stellen fest, dass
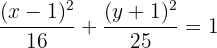
4 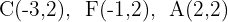
Der Wert für  ist die Distanz zwischen dem Mittelpunkt und dem Scheitelpunkt A. Der Wert für
ist die Distanz zwischen dem Mittelpunkt und dem Scheitelpunkt A. Der Wert für  ist die Distanz zwischen dem Mittelpunkt und dem Brennpunkt. Somit gilt:
ist die Distanz zwischen dem Mittelpunkt und dem Brennpunkt. Somit gilt:

Die Werte  ,
,  und
und  stehen in einem pythagoreischen Verhältnis, das heißt
stehen in einem pythagoreischen Verhältnis, das heißt
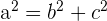
Wir formen entsprechend um, um den Wert für  zu berechnen
zu berechnen

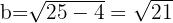
Wir stellen fest, dass
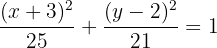
Schreibe die Normalform der Ellipsengleichung mit dem Mittelpunkt im Ursprungspunkt, die durch den Punkt  verläuft und deren Nebenachse die Länge
verläuft und deren Nebenachse die Länge  hat und sich auf der
hat und sich auf der  -Achse befindet.
-Achse befindet.
Die Länge der Nebenachse beträgt 

Der Mittelpunkt liegt im Ursprungspunkt und die Nebenachse auf der y-Achse. Deshalb hat die Normalgleichung folgende Form
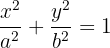
Da der Punkt (2,1) auf der Ellipse liegt, erfüllen die Koordinaten die Gleichung in der Normalform

Wir formen entsprechend um, um den Wert für  zu bestimmen
zu bestimmen
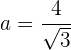
Da die Werte  und
und  bekannt sind, kommen wir zu dem Schluss, dass
bekannt sind, kommen wir zu dem Schluss, dass
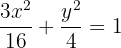
Die Brennstrecke einer Ellipse mit dem Mittelpunkt im Ursprungspunkt beträgt  . Ein Punkt der Ellipse ist von ihren Brennpunkten
. Ein Punkt der Ellipse ist von ihren Brennpunkten  bzw.
bzw.  entfernt. Berechne die Normalform dieser Ellipse, wenn die Hauptachse auf der
entfernt. Berechne die Normalform dieser Ellipse, wenn die Hauptachse auf der  -Achse liegt.
-Achse liegt.
Die Brennstrecke entspricht dem Wert für 

Wir erinnern uns daran, dass die Summe der Abstände zwischen einem Punkt auf der Ellipse und den Brennpunkten gleich  ist
ist

Die Werte  ,
,  und
und  stehen in einem pythagoreischen Verhältnis, das heißt
stehen in einem pythagoreischen Verhältnis, das heißt
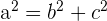
Wir formen entsprechend um, um den Wert für  zu bestimmen
zu bestimmen

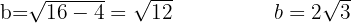
Da die Werte für  und
und  bekannt sind, kommen wir zu dem Schluss, dass
bekannt sind, kommen wir zu dem Schluss, dass

Schreibe die Normalform der Gleichung der Ellipse, die durch folgende Punkte verläuft:

Die Ellipse verläuft durch die Punkte:  . Somit erfüllen ihre Koordinaten die Normalform der Ellipsengleichung. Das heißt
. Somit erfüllen ihre Koordinaten die Normalform der Ellipsengleichung. Das heißt
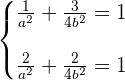
Wir lösen das System

Dann
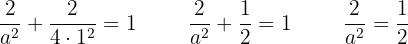
Wir bestimmen 

Schließlich
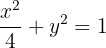
Bestimme die Normalform der Ellipsengleichung mit dem Mittelpunkt im Ursprungspunkt und der Hauptachse auf der  -Achse, deren Brennstrecke
-Achse, deren Brennstrecke  beträgt. Die Fläche des Rechtecks, dessen Seiten die gleichen Maße wie die Achsen (Haupt- und Nebenachsen) haben, beträgt
beträgt. Die Fläche des Rechtecks, dessen Seiten die gleichen Maße wie die Achsen (Haupt- und Nebenachsen) haben, beträgt  u².
u².
Da die Seiten des Rechtecks die Achsen sind und ihre Längen  und
und  entsprechen, gilt
entsprechen, gilt
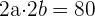
Die Brennstrecke entspricht 

Die Werte  ,
,  und
und  stehen in einem pythagoreischen Verhältnis, das heißt
stehen in einem pythagoreischen Verhältnis, das heißt

Daraus ergibt sich ein System aus zwei Gleichungen
Mit der ersten Gleichung ermitteln wir  und mit der zweiten
und mit der zweiten 
Wir nehmen  aus der zweiten Gleichung, und setzen es in die erste Gleichung ein
aus der zweiten Gleichung, und setzen es in die erste Gleichung ein
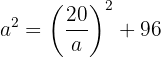
Wir lösen auf
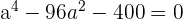
Wir lösen mit der allgemeinen Formel und erhalten den Wert für 

Da die Werte  und
und  bekannt sind, kommen wir zu dem Schluss, dass
bekannt sind, kommen wir zu dem Schluss, dass

Bestimme die Koordinaten
Bestimme die Koordinaten des Mittelpunkts der Sehne, die die folgende Gleichung schneidet: 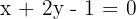 in der Ellipsengleichung:
in der Ellipsengleichung: 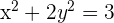 .
.
1 Bestimme die Schnittpunkte
Die Schnittpunkte sind diejenigen, die das Gleichungssystem der Geraden und der Ellipse lösen.
Zur Lösung können wir  aus der ersten Gleichung entfernen und quadrieren. Wir entfernen auch
aus der ersten Gleichung entfernen und quadrieren. Wir entfernen auch  in der zweiten Gleichung
in der zweiten Gleichung
Wir setzen beide Gleichungen gleich
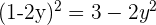
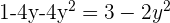
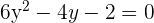
Um die Lösungen zu bestimmen, wenden wir die allgemeine Formel an
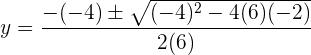
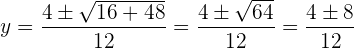
Die Lösungen für die Koordinate  sind
sind
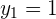
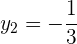
Die Koordinaten  werden mithilfe eines Gleichungssystems berechnet. In diesem Fall nutzen wir
werden mithilfe eines Gleichungssystems berechnet. In diesem Fall nutzen wir
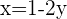
Die Schnittpunkte sind also gegeben durch
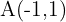
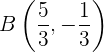
2 Den Mittelpunkt ermitteln
Der Mittelpunkt zwischen den Punkten A und B ist gegeben durch
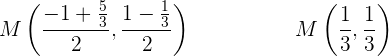
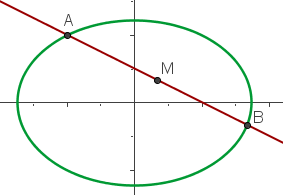
Mit KI zusammenfassen:













