Wenn 
und 
an 
ableitbar sind, so gilt als Wendepunkt , wenn erfüllt ist, dass:
1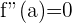 
2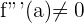 
Berechnung der Wendepunkte
Um die Wendepunkte zu finden, gehst Du wie folgt vor:
1 Finde die zweite Ableitung und berechne ihre Wurzeln.
2 Führe die dritte Ableitung durch und berechne den Wert, der von den Nullstellen der zweiten Ableitung eingenommen wird
3 Wenn das Ergebnis von Null verschieden ist, hast Du einen Wendepunkt.
4 Berechne die Bildmenge des Wendepunkts.
Beispiel:
Finde die Wendepunkte von 
1 Finde die zweite Ableitung und berechne ihre Wurzeln.
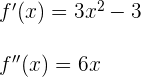
ist die einzige Wurzel von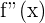 
2 Führe die dritte Ableitung durch und berechne den Wert, der von den Nullstellen der zweiten Ableitung eingenommen wird
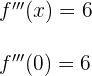
3 Da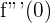 
ungleich Null ist, hast Du einen Wendepunkt.
4 Berechne die Bildmenge des Wendepunkts.
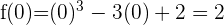
Die Funktion hat einen Wendepunkt bei 
Wendepunkte aus Konkavität und Konvexität
Da Du Dich bereits mit der Konkavität und Konvexität einer Funktion beschäftigt hast, wird es folgendes geben:
Wendepunkte an den Stellen, an denen sie von konkav zu konvex oder andersrum wird.
Beispiel:
Finde die Wendepunkte von 
1 Finde den Bereich der Funktion, d. h. die Werte, bei denen der Nenner ungleich Null ist. Da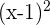 
sich für 
aufhebt, ist der Bereich:
2 Finde die zweite Ableitung und berechne ihre Wurzeln.
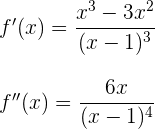
ist die einzige Wurzel von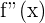
3 Die Wurzel von 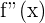unterteilt den Bereich in drei Teile, die konkav oder konvex sein können
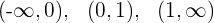
4 Prüfe die Konkavität und Konvexität für jedes Intervall, dazu nimmst du einen Vertreter und wertest ihn in 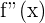aus
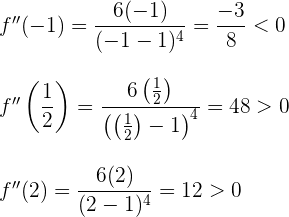
es cóncava en 
y convexa en 
.
5 Du hast einen Wendepunkt bei , da die Funktion von konkav zu konvex wechselt.
6 Berechne die Bildmenge des Wendepunkts.
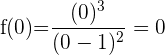
Die Funktion hat einen Wendepunkt bei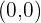 
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
