Kapitel

Konstante Funktionen
Sie haben die Form
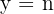 ,
,
wobei:
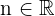 .
.
Die Steigung ist  .
.
Der Graph ist eine horizontale Gerade parallel zur x-Achse.
Funktionen 1. Grades
Lineare Funktion
Sie hat die Form
 ,
,
wobei:
 die Steigung ist, also die Neigung der Geraden in Bezug auf die x-Achse.
die Steigung ist, also die Neigung der Geraden in Bezug auf die x-Achse.
Ihr Graph ist eine Gerade, die durch den Koordinatenursprung verläuft.
Identitätsfunktion
Sie hat die Form
 ,
,
wobei:
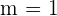 .
.
Ihr Graph ist die Winkelhalbierende des ersten und dritten Quadranten.
Affine Funktion
Sie hat die Form
 ,
,
wobei:
 die Steigung ist, also die Neigung der Geraden in Bezug auf die x-Achse.
die Steigung ist, also die Neigung der Geraden in Bezug auf die x-Achse.
 ist die Ordinate im Ursprung und gibt den Punkt an, an dem die Gerade die y-Achse schneidet.
ist die Ordinate im Ursprung und gibt den Punkt an, an dem die Gerade die y-Achse schneidet.
Vertikale Geraden
Sie haben die Form:
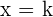
Geraden, die parallel zur y-Achse verlaufen, sind keine Funktionen, da ein Wert von  unendlich viele Abbildungen hat und als Funktion nur eine haben kann.
unendlich viele Abbildungen hat und als Funktion nur eine haben kann.
Quadratische Funktion
Es handelt sich um Polynomfunktionen zweiten Grades, deren Graph eine Parabel ist.
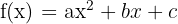
Um eine Parabel grafisch darzustellen, muss man Folgendes wissen:
Scheitelpunkt
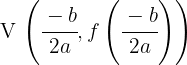
Die Symmetrieachse der Parabel verläuft durch diesen Punkt.
Die Gleichung der Symmetrieachse lautet:
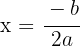
Schnittpunkte mit der  -Achse
-Achse
Auf der x-Achse ist die zweite Koordinate gleich 0, also gilt:
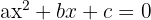
Wir lösen die Gleichung und erhalten:
1 Zwei Schnittpunkte: 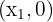 und
und 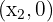 , wenn
, wenn 
2 Einen Schnittpunkt: 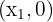 , wenn
, wenn 
3 Keinen Schnittpunkt, wenn 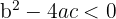
Schnittpunkte mit der  -Achse
-Achse
Auf der y-Achse ist die erste Koordinate gleich 0, also haben wir:
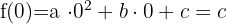
Somit ist der Schnittpunkt 
Rationale Funktionen
Das Kriterium ist durch einen Quotienten aus Polynomen gegeben:
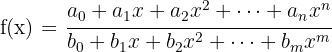
Der Definitionsbereich sind alle reellen Zahlen außer den Werten von  , für die der Nenner 0 wird.
, für die der Nenner 0 wird.
Innerhalb dieses Typs haben wir die Funktionen der umgekehrten Proportionalität der Gleichung:
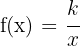 .
.
Wurzelfunktionen
Das Kriterium ist durch die Variable  unter dem Wurzelzeichen gegeben.
unter dem Wurzelzeichen gegeben.
Abschnittsweise definierte Funktionen
Es handelt sich um Funktionen, die je nach den betrachteten Intervallen durch unterschiedliche Kriterien definiert sind.
Betragsfunktionen
Durch folgende Schritte werden aus Betragsfunktionen abschnittsweise definierte Funktionen:
1 Die Funktion wird gleich 0 gesetzt, ohne den Betrag, und die Nullstellen werden berechnet.
2 Es werden Intervalle mit den Nullstellen gebildet und das Vorzeichen des jeweiligen Intervalles ausgewertet.
3 Wir definieren die Funktion abschnittsweise und denken dabei daran, dass für die Intervalle, auf denen  negativ ist, sich das Vorzeichen der Funktion ändert.
negativ ist, sich das Vorzeichen der Funktion ändert.
4 Wir stellen die resultierende Funktion grafisch dar.
Exponentialfunktion
 sei eine positive reelle Zahl. Die Funktion, die jeder reellen Zahl
sei eine positive reelle Zahl. Die Funktion, die jeder reellen Zahl  mit der Potenz
mit der Potenz 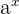 entspricht, heißt Exponentialfunktion mit Basis
entspricht, heißt Exponentialfunktion mit Basis  und Exponent
und Exponent  .
.
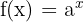
Logarithmusfunktion
Die Logarithmusfunktion zur Basis  ist die Umkehrung der Exponentialfunktion zur Basis
ist die Umkehrung der Exponentialfunktion zur Basis  .
.
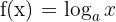
Trigonometrische Funktionen
Sinusfunktion
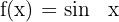
Kosinusfunktions
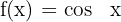
Tangensfunktion
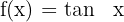
Kotangensfunktion
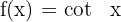
Sekansfunktion
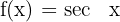
Kosekansfunktion
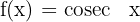
Mit KI zusammenfassen:












