Die affine Funktion ist von der Art:
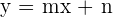
wobei:
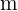die Höhe der Geraden ist.
Die Steigung ist die Neigung der Geraden auf die Abszissenachse.
Zwei parallele Geraden haben die gleiche Steigung.
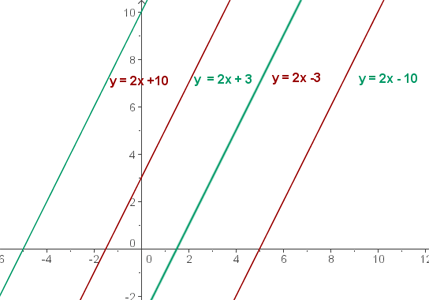
ist die Ordinate zum Ursprung der Geraden und gibt den Punkt an, an dem die Gerade die Ordinatenachse schneidet.
Ihr Graph ist eine Gerade, die nicht durch den Koordinatenursprung verläuft.
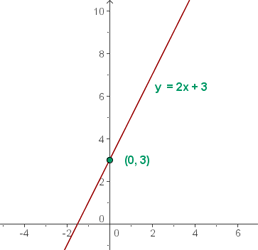
Um die Funktion darzustellen, gibst Du ihr mindestens zwei Werte
Beispiele:
1 Stelle 
grafisch dar
Gib Werte für die Funktion
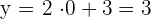
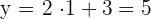
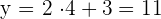
Du erhältst die folgende Wertetabelle
 |  |  |  |  |  |
|---|---|---|---|---|---|
 | |  |  |  |  |
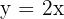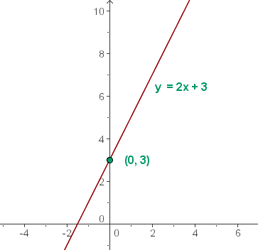
Der Punkt (0, 3) ist die Ordinate im Ursprung.
2 Stelle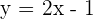 
grafisch dar
Gib Werte für die Funktion
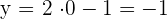
Du erhältst die folgende Wertetabelle
|  |
|---|---|
|  |
| |
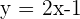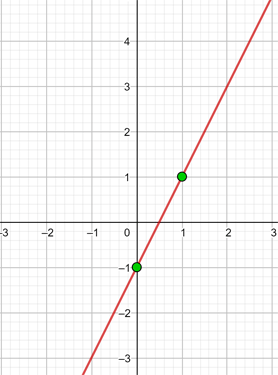
Der Punkt 
ist die Ordinate im Ursprung.
3 Stelle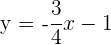 
grafisch dar
Gib Werte für die Funktion
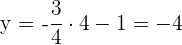
Du erhältst die folgende Wertetabelle
|  |
|---|---|
| |
|  |
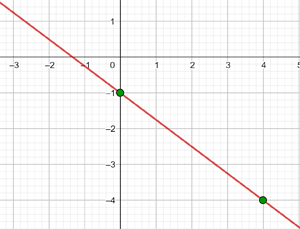
Der Punkt ist die Ordinate im Ursprung.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
