Willkommen in unserem Bereich, der sich mit Übungen zur mittleren absoluten Abweichung befasst. Die mittlere absolute Abweichung ist ein statistisches Maß, das uns ein quantitatives Verständnis der Streuung oder Variabilität eines Datensatzes im Verhältnis zu seinem arithmetischen Mittel vermittelt. In dieser Reihe von Übungen werden wir verschiedene Szenarien und Datensätze untersuchen, um die mittlere absolute Abweichung zu berechnen und zu verstehen.
Bei diesen Aufgaben wirst du mit praktischen Situationen und konkreten Daten konfrontiert, so dass du das Konzept der mittleren absoluten Abweichung effektiv anwenden kannst. Dieses Konzept ist in der Statistik von entscheidender Bedeutung, da es Informationen über die durchschnittliche Streuung der Daten in Bezug auf den Mittelwert liefert, was für das Verständnis der Variabilität in realen Datensätzen wesentlich ist.
Bei der Lösung dieser Aufgaben entwickelst du die Fähigkeit, die mittlere absolute Abweichung zu berechnen, die Ergebnisse zu interpretieren und dieses Wissen in einer Vielzahl von Kontexten anzuwenden. Mach dich bereit, die Variabilität in Datensätzen zu erforschen und deine analytischen Fähigkeiten in der Statistik zu verbessern.
Ermittle die mittlere absolute Abweichung der folgenden Mengen von Zahlen:
a.  .
.
b. 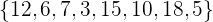 .
.
c. 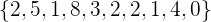 .
.
a. 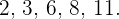
Mittelwert:
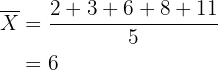
Mittelere absolute Abweichung:

b. 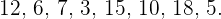
Mittelwert:

Mittlere absolute Abweichung:
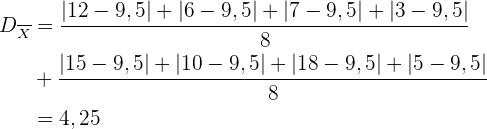
c. 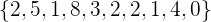 .
.
Mittelwert:
 .
.
Mittlere absolute Abweichung:
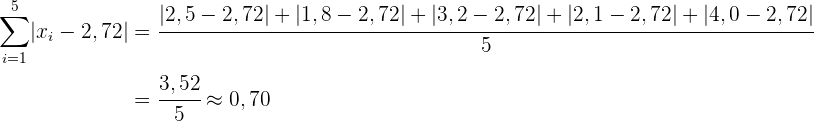
Ermittle den Mittelwert und die mittlere absolute Abweichung der Menge der Zahlen 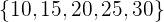 . Ersetze im Anschluss den Wert 15 durch den Wert 30, um die Menge der Zahlen
. Ersetze im Anschluss den Wert 15 durch den Wert 30, um die Menge der Zahlen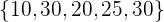 zu erhalten. Berechne den Mittelwert und die mittlere absolute Abweichung, und vergleiche sie mit der Vorherigen.
zu erhalten. Berechne den Mittelwert und die mittlere absolute Abweichung, und vergleiche sie mit der Vorherigen.
Mittelwert:
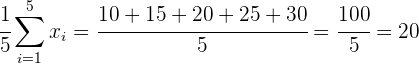 .
.
Mittlere absolute Abweichung:
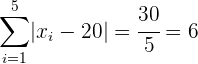 .
.
Nun machen wir es mit der zweiten Menge der Zahlen: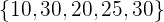
Mittelwert:
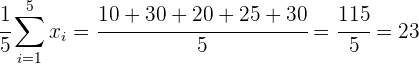 .
.
Mittlere absolute Abweichung:
 .
.
Obwohl es so aussieht, als ob sich die Menge der Zahlen durch Ersetzen der 15 durch die 30 stabilisiert, erhöht sich die mittlere absolute Abweichung durch das Beibehalten der 10.
Gegeben ist eine Menge von Zahlen 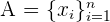 . Was passiert mit der mittleren absoluten Abweichung von A, wenn zu jedem der Elemente eine Zahl
. Was passiert mit der mittleren absoluten Abweichung von A, wenn zu jedem der Elemente eine Zahl  addiert wird?
addiert wird?
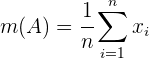
sei der Mittelwert von  . Die mittlere absolute Abweichung ist somit
. Die mittlere absolute Abweichung ist somit
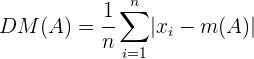
Nun stellen wir fest, dass wir durch Änderung der Menge  die Menge
die Menge
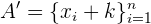 erhalten,
erhalten,
deren Mittelwert
 ist.
ist.
Nun ist die neue mittlere absolute Abweichung
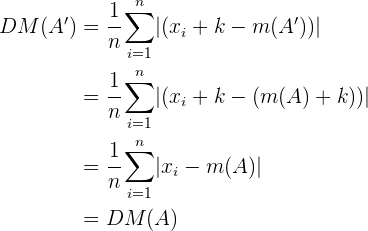
Das heißt, die mittlere absolute Abweichung ist bei einer Veränderung der Menge invariant.
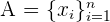 sei eine Menge von Zahlen. Was passiert mit der mittleren absoluten Abweichung von A, wenn jedes Element mit einer Zahl
sei eine Menge von Zahlen. Was passiert mit der mittleren absoluten Abweichung von A, wenn jedes Element mit einer Zahl  multipliziert wird?
multipliziert wird?
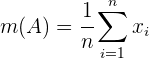
sei der Mittelwert von  . Somit ist die mittlere absolute Abweichung
. Somit ist die mittlere absolute Abweichung
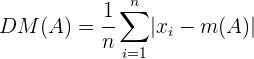
Nun stellen wir fest, dass wir durch Änderung der Menge  die Menge
die Menge
 ,
,
deren Mittelwert
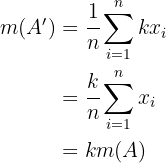 ist.
ist.
Die neue mittlere absolute Abweichung ist somit

Das heißt, die mittlere absolute Abweichung einer Erweiterung der Menge hat den Effekt, dass sie mit dem absoluten Wert des Erweiterungskoeffizienten multipliziert wird.
Berechne die mittlere absolute Abweichung einer statistischen Verteilung, die in der folgenden Tabelle angegeben ist:
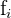 | |
|---|---|
 |  |
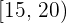 |  |
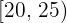 |  |
 |  |
 |  |
Wir fügen eine weitere Spalte mit den Produkten der Klassenmerkmale durch ihre entsprechenden absoluten Häufigkeiten hinzu und führen die Addition durch (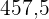 )
)
Wir fügen eine weitere Spalte hinzu, in der die Produkte der Abweichungen vom Mittelwert mit den entsprechenden absoluten Häufigkeiten aufgeführt sind 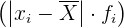 und berechnen die Summe (
und berechnen die Summe (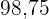 )
)
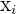 | 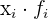 | 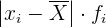 | |
|---|---|---|---|
 | 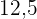 |  |  |
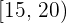 | 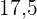 | 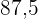 |  |
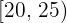 | 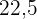 | 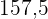 | 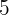 |
 | 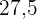 | 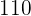 |  |
 | 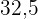 |  |  |
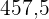 |  |
Mittelwert:
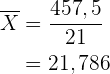
Mittlere absolute Abweichung:
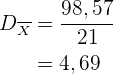
Mit KI zusammenfassen:


