Die Zusammensetzung von Funktionen ist ein grundlegendes Konzept in der Mathematik, insbesondere in der Infinitesimalrechnung und der Algebra. Sie besteht darin, zwei Funktionen so zu kombinieren, dass die Ausgabe der einen als Eingabe für die andere fungiert. Mathematisch wird sie mit 
angegeben, was bedeutet, dass zuerst die Funktion 
angewendet wird und dann die Funktion 
auf das erhaltene Ergebnis angewendet wird.
Dieser Prozess ist wichtig, um zu verstehen, wie Funktionen zusammenwirken, und ermöglicht die Lösung einer Vielzahl von Problemen, bei denen Variablen in einer verketteten Weise voneinander abhängen. In dieser Reihe von Übungsaufgaben werden verschiedene Situationen behandelt, in denen die Zusammensetzung von Funktionen durchgeführt wird, mit dem Ziel, das Verständnis und die Fähigkeit zur Handhabung dieser Art von Operationen zu stärken.
Gegeben sind die Funktionen:
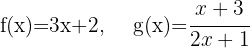
Berechne:
a 
b 
a
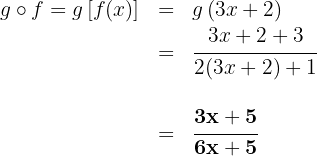
b
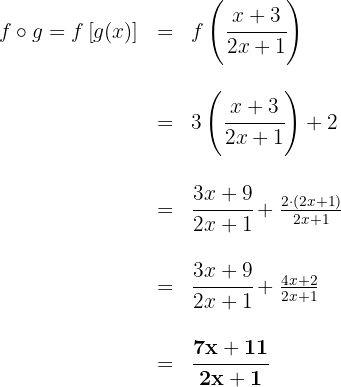
Gegeben sind die Funktionen:
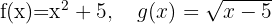
Berechne:
a
b
a
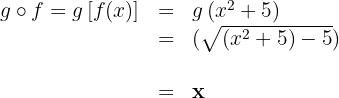
b
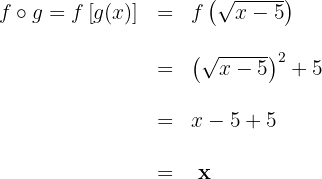
Gegeben sind die Funktionen:
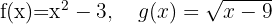
Berechne:
a
b
a
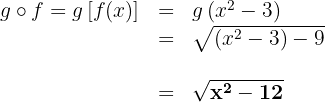
b
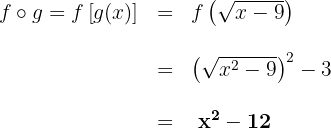
Gegeben sind die Funktionen:
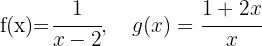
Berechne:
a
b
a
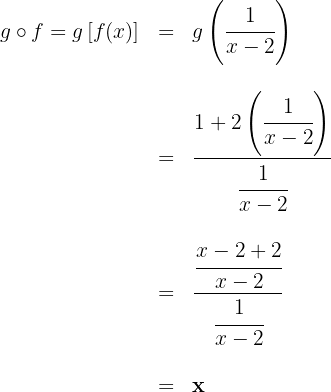
b
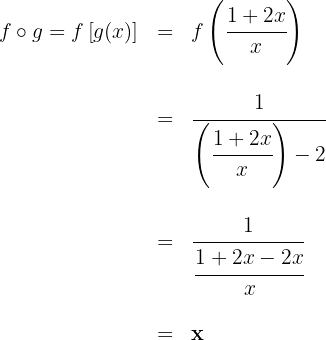
Gegeben sind die Funktionen:
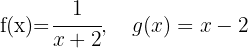
Berechne:
a
b
a
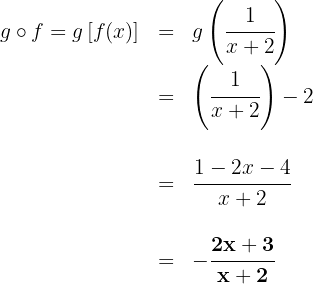
b
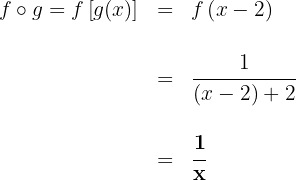
Gegeben sind die Funktionen:
Berechne:
a
b
a
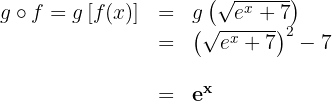
b
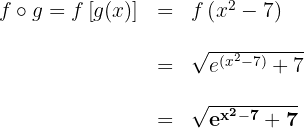
Gegeben sind die Funktionen:
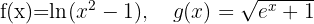
Berechne:
a
b
a
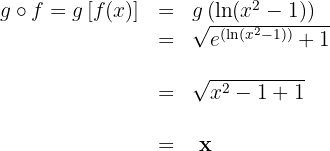
b
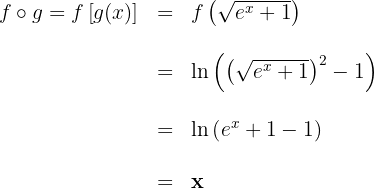
Gegeben sind die Funktionen:
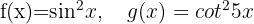
Berechne:
a
b
a
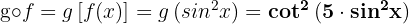
b
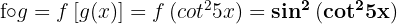
Gegeben sind die Funktionen:
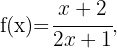
Berechne:
a
b
c 
d Überprüfe: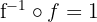 
a
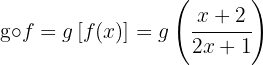
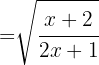
b
c
Um zu berechnen, schreiben wir die Funktion 
wie folgt:
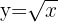
Wir ermitteln 
Wir ändern in und 
in
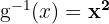
d Überprüfe: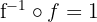
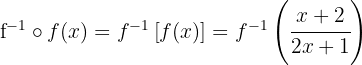
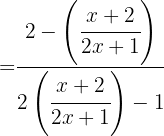
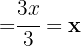
Die Zusammensetzung einer Funktion mit der Umkehrfunktion entspricht der identischen Abbildung
Gegeben sind die Funktionen:
, 
, 
Berechne:
a
b
c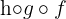 
d 
e 
f Überprüfe: 
g Überprüfe: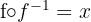 
a
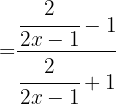
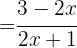
b
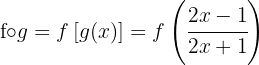
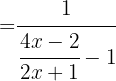
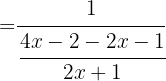
c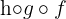
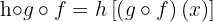
Wir wissen bereits, dass 
,
weshalb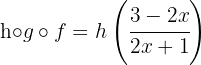 
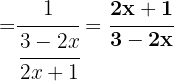
d
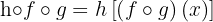
Wir wissen bereits, dass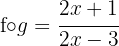 
,
weshalb 
e
Um zu berechnen, schreiben wir die Funktion wie folgt:
und ermitteln die Variable
Wir ändern in und in
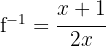
f Wir überprüfen:
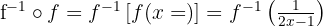
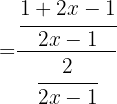
g Überprüfe: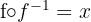
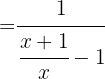
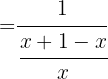
Die Zusammensetzung einer Funktion mit der Umkehrfunktion entspricht der identischen Abbildung
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
