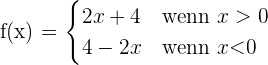
Wir stellen fest, dass wir im Intervall 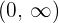 — also auf der rechten Seite der Ebene — die Funktion
— also auf der rechten Seite der Ebene — die Funktion 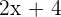 haben.
haben.
Im Intervall auf der anderen Seite  — linke Seite der Ebene — haben wir die Funktion
— linke Seite der Ebene — haben wir die Funktion 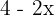 .
.
Daher sieht der Graph wie in der folgenden Abbildung aus:
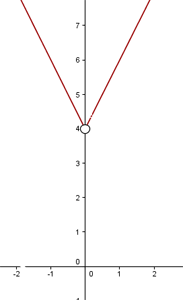
Wie oben erwähnt, ist die Funktion definiert für 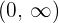 und
und  . Die Definitionsmenge ist also
. Die Definitionsmenge ist also
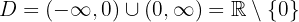
Andererseits können wir aus der Abbildung ersehen, dass die Wertemenge wie folgt ist
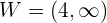
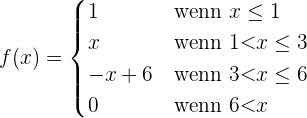
Beachte, dass die Funktion für vier verschiedene Bereiche definiert ist. Als Erstes hat sie für das Intervall 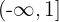 den Wert
den Wert
1. Für das Intervall 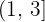 hat sie den Wert
hat sie den Wert  und so weiter.
und so weiter.
Daher sieht der Graph wie in der folgenden Abbildung aus:
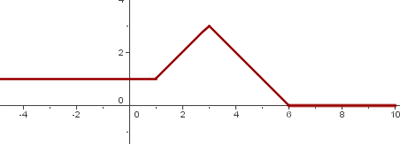
Die Definitionsmenge ist
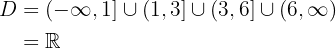
Die Wertemenge ist
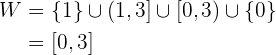
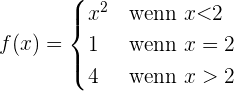
Wenn wir die Ausdrücke für die einzelnen Bereiche einzeichnen, ergibt sich folgender Graph:
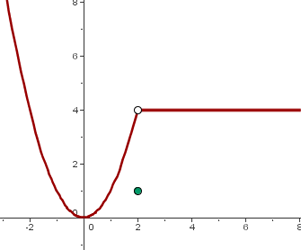
Außerdem ist die Definitionsmenge gegeben durch

Die Wertemenge ist gegeben durch
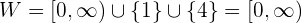
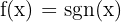
Beachte, dass 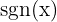 die Vorzeichenfunktion ist, die wie folgt definiert ist
die Vorzeichenfunktion ist, die wie folgt definiert ist
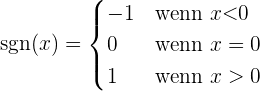
Der Graph ist somit durch folgende Abbildung gegeben:
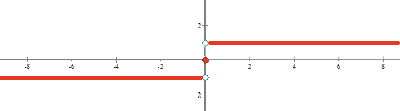
Außerdem ist die Definitionsmenge
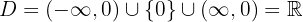
Die Wertemenge ist

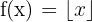
Beachte, dass 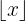 die Abrundungsfunktion ist und als die größte ganze Zahl
die Abrundungsfunktion ist und als die größte ganze Zahl  definiert ist, sodass
definiert ist, sodass 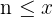 . Zum Beispiel:
. Zum Beispiel:
1 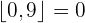
2 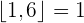
3 
4 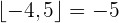
Daher sieht der Graph wie folgt aus:
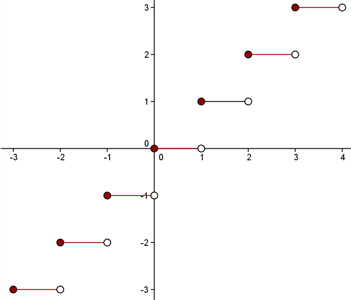
Die Definitionsmenge der Funktion ist

Die Wertemenge ist
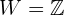

Von jedem  subtrahieren wir
subtrahieren wir 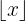 , welcher der ganzzahlige Teil ist. Das Ergebnis von
, welcher der ganzzahlige Teil ist. Das Ergebnis von  ist der Dezimalteil von
ist der Dezimalteil von  . Der Graph sieht daher wie folgt aus:
. Der Graph sieht daher wie folgt aus:
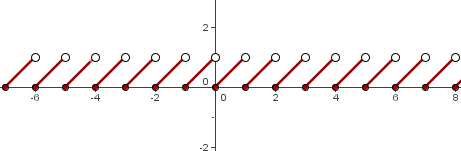
Wir stellen außerdem fest, dass Folgendes erfüllt ist
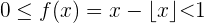
Die Definitionsmenge ist gegeben durch 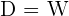 und die Wertemenge durch
und die Wertemenge durch
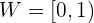

Wir stellen fest, dass diese Funktion genau dieselbe ist wie die vorhergehende, jedoch wird hier 1 addiert. Der Graph sieht also wie folgt aus
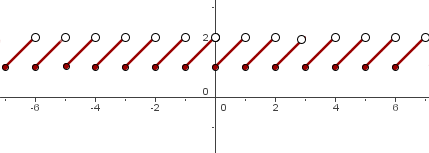
Die Definitionsmenge ist dieselbe, nämlich 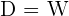 ; die Wertemenge ist jedoch
; die Wertemenge ist jedoch
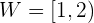
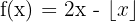
Diese Funktion kann als 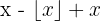 betrachtet werden. Daher wird die Funktion des Dezimalteils von
betrachtet werden. Daher wird die Funktion des Dezimalteils von  mit
mit  addiert. Es ergibt sich folgender Graph:
addiert. Es ergibt sich folgender Graph:
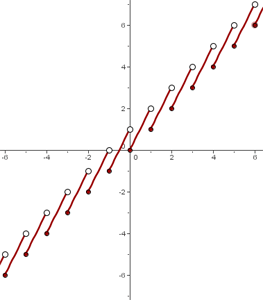
Und die Definitionsmenge ist ebenfalls 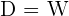 ; die Wertemenge ist nun aber
; die Wertemenge ist nun aber 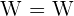 (was aus der Abbildung ersichtlich ist).
(was aus der Abbildung ersichtlich ist).

Nun dividieren wir zunächst durch 2 und erhalten dann den ganzzahligen Teil. Es handelt sich also um eine Art "Skalierung" der Abrundungsfunktion. Es ist, als ob wir den Graphen horizontal strecken würden.
Der Graph sieht wie folgt aus:
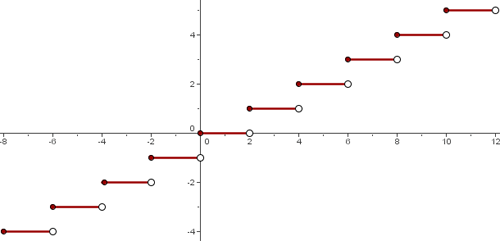
Die Definitionsmenge und die Wertemenge sind jedoch dieselben wie bei der Abrundungsfunktion.:

und
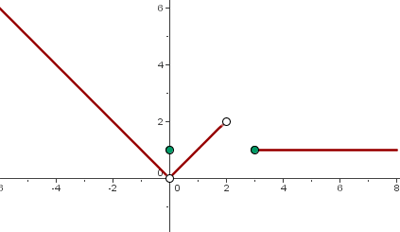
Sieh dir den folgenden Graphen an und bestimme den analytischen Ausdruck der Funktion, die er beschreibt.
 ist die abschnittsweise definierte Funktion. Die Funktionen
ist die abschnittsweise definierte Funktion. Die Funktionen 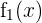 ,
, 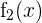 etc. sind Hilfsfunktionen, die in Teilen der Definitionsmenge definiert sind.
etc. sind Hilfsfunktionen, die in Teilen der Definitionsmenge definiert sind.
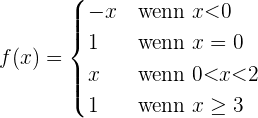
1 Zunächst stellen wir fest, dass wir im Intervall  eine Gerade mit negativer Steigung haben. Es handelt sich um folgende Funktion:
eine Gerade mit negativer Steigung haben. Es handelt sich um folgende Funktion:
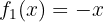
2 Außerdem ist 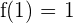 .
.
3 Wir haben im Intervall  die Funktion
die Funktion  .
.
4 Die Funktion ist im Intervall 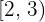 nicht definiert.
nicht definiert.
5 Und im Intervall 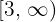 ist die Funktion konstant:
ist die Funktion konstant:
Die Funktion ist also gegeben durch
Mit KI zusammenfassen:



