Aufgaben zur Darstellung von algebraischen Funktionen

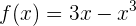
Definitionsbereich: Wir denken daran, dass wir je nach Art der Funktion den Definitionsbereich bestimmen können. In diesem Fall ist este caso 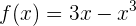eine Polynomfunktion und ihr Definitionsbereich sind somit alle reellen Zahlen:
Symmetrie: Um die Symmetrie zu überprüfen, untersuchen wir zunächst die Funktion für 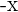aus und erhalten 3 mögliche Fälle:
1 Eine gerade Funktion, wenn ,
2 Eine ungerade Funktion, wenn ,
3 oder nicht anwendbar, wenn wir nicht zur Ausgangsfunktion zurückkehren. In diesem Fall 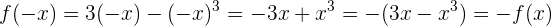Daher haben wir eine Symmetrie zum Ursprung, d.h. eine ungerade Funktion

Schnittpunkte mit den Achsen

Schnittpunkt mit der -Achse:

Wir haben einen Schnittpunkt mit dieser Achse, wenn 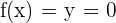. Wir beginnen also, indem wir gleich 0 setzen

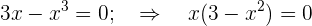
Daher erhalten wir 0, wenn

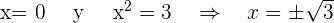
Daraus folgt, dass die Schnittpunkte mit der -Achse wie folgt sind:

Schnittpunkt mit der -Achse:

Wir haben Schnittpunkte mit dieser Achse, wenn . Somit:

.

Deshalb ist der Schnittpunkt mit der -Achse:

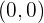
Asymptoten

Um die Asymptoten zu finden, müsste man einen Punkt finden, sodass .

In diesem Fall haben wir eine Polynomfunktion, die keine Asymptoten hat.

Monotonieverhalten

Um zu wissen ob eine Funktion an einem Punkt steigt oder fällt, müssen wir die kritischen Punkte ermitteln. Also die Stellen, an denen die Ableitung 0 wird. Wir berechnen die Ableitung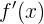

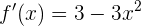
Wir berechnen die kritischen Punkte

Nun überprüfen wir, welches Vorzeichen die Funktion hat, wenn wir den Definitionsbereich wie folgt unterteilen: und :

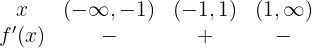
Die Funktion steigt also im Intervall 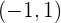und fällt im Intervall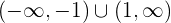

Um die Minima und Maxima zu bestimmen, untersuchen wir die vorher mit der 2. Ableitung ermittelten kritischen Punkte. Wenn sie positiv ist, haben wir ein Minimum und wenn sie negativ, ist, haben wir ein Maximum.

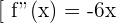
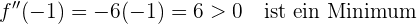
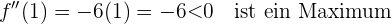
Wir haben also ein Minimum bei 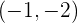und ein Maximum bei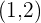

Konkavität und Konvexität
Um zu ermitteln, ob die Funktion konkav und kovex ist, nehmen wir die 2. Ableitung und überprüfen, wann sie 0 wird. Wir prüfen die Intervalle, in denen die Funktion positiv und negativ ist; ist sie positiv, ist sie konvex, ist sie negativ, ist sie konkav.

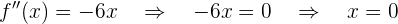
und in den Intervallen

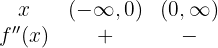
Die Funktion ist somit konvex im Intervall 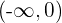und konkav im Intervall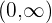

Wendepunkte
Es gibt einen Wendepunkte, wenn an einem Punkt Folgendes gilt:

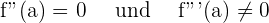
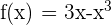
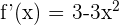
Wir untersuchen nun den einzigen Punkt, an dem die 2. Ableitung 0 wird

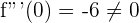
Wenn das Ergebnis ungleich 0 ist, haben wir einen Wendepunkt bei .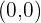

Grafische Darstellung

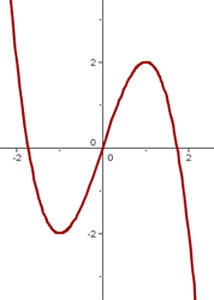
Definitionsbereich:
Symmetrie: Wir stellen fest, dass 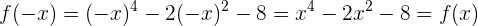. Es liegt also Symmetrie zur -Achse vor, das heißt, die Funktion ist gerade.
Schnittpunkte mit den AchsenSchnittpunkte mit der -Achse:

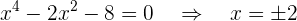
Die Schnittpunkte sind also

Schnittpunkte mit der -Achse:

Wir stellen fest, dass

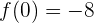
Der Schnittpunkt ist also

Asymptoten

Sie hat keine Asymptoten.

Monotonieverhalten

Wir berechnen die kritischen Punkte:

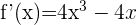
wir setzen gleich 0

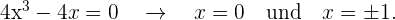
Nun überprüfen wir das Vorzeichen in den folgenden Segmenten des Definitionsbereichs:

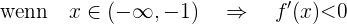
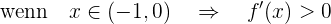
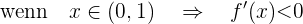
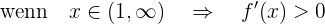
Sie steigt also im Intervall und fällt im Intervall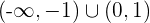

Wir untersuchen die kritischen Punkte, die wir mit der 2. Ableitung berechnen und erhalten

Die Tiefpunkte sind

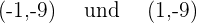
Der Hochpunkt ist

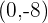
Konkavität und Konvexität

Wir suchen die Punkte, an denen die zweite Ableitung 0 wird

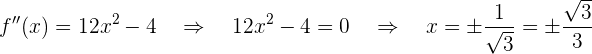
Wir stellen fest, dass

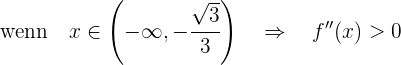
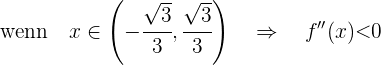
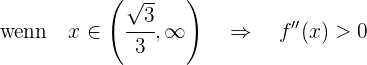
Sie ist also konvex im Intervall 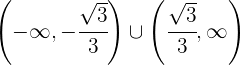und konkav im Intervall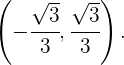

Wendepunkte

Durch Berechnung der 3. Ableitung ergibt sich, dass die Wendepunkte wie folgt lauten

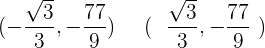
Grafische Darstellung

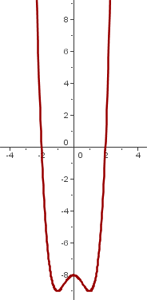
Definitionsbereich
Wir eliminieren den Punkt, an dem der Nenner 0 wird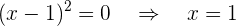
Somit: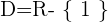
Symmetrie: Da , liegt keine Symmetrie vor.
Schnittpunkte mit den AchsenSchnittpunkte mit der -Achse

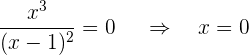
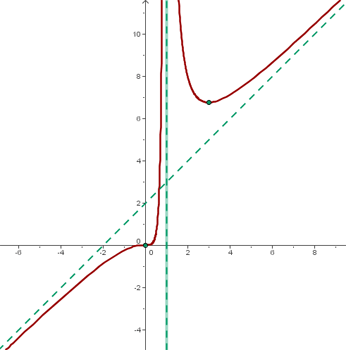
Der Schnittpunkt ist somit

Schnittpunkt mit der -Achse

Wir haben

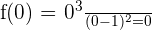
Der Schnittpunkt ist also

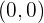
Asymptoten

Horizontale Asymptote:

Horizontale Asymptoten sind horizontale Geraden, denen sich die Funktion endlos nähert. Horizontale Asymptoten sind Geraden der Gleichung: .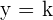

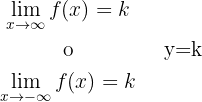
Wir stellen fest, dass

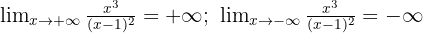
Sie hat also keine horizontalen Asymptoten.

Vertikale Asymptoten:

Vertikale Asymptoten sind vertikale Geraden, denen sich die Funktion endlos nähert, ohne sie jemals zu schneiden. Vertikale Asymptoten sind Geraden der Gleichung: .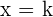

Wir stellen fest, dass

und somit

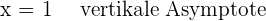
Schiefe Asymptote:

Schiefe Asymptoten sind Geraden der Gleichung:

,

wobei

Schiefe Asymptoten werden nur dann gefunden, wenn es keine horizontalen Asymptoten gibt.

In diesem Fall:

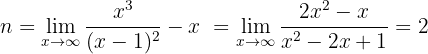
Somit hat die schiefe Asymptote die Gleichung:

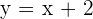
Monotonieverhalten

Zunächst ermitteln wir die kritischen Punkte

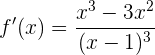
Wir setzen gleich 0

Die kritischen Punkte sind

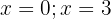
Nun überprüfen wir das Vorzeichen in den folgenden Segmenten des Definitionsbereichs:

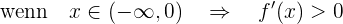
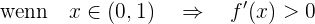
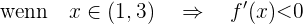
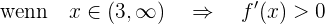
somit

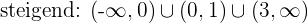
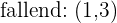
Wir untersuchen die kritischen Punkte, die wir mit der 2. Ableitung ermitteln, und erhalten

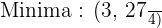
Konkavität und Konvexität

Wir berechnen die 2. Ableitung und ermitteln, wann sie 0 wird

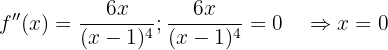
Wir untersuchen in engen Intervallen

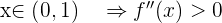
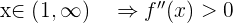
Sie ist also konvex im Intervall und konkav im Intervall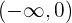

Wendepunkte

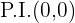
Grafische Darstellung

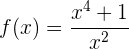
Definitionsbereich
Wir eliminieren den Punkt, an dem der Nenner 0 wird
Symmetrie: Wir stellen fest, dass 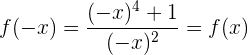. Somit liegt Symmetrie zur -Achse vor. Die Funktion ist also gerade.
Schnittpunkte mit den AchsenSchnittpunkte mit der -Achse:

Wir setzen gleich 0 und erhalten

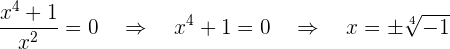
Es gibt also keine Schnittpunkte mit der -Achse

Schnittpunkt mit der -Achse:

Ähnlich

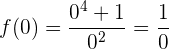
Somit gibt es keine Schnittpunkte mit der -Achse

Asymptoten

Horizontale Asymptote:

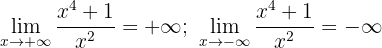
Das heißt, es gibt keine horizontale Asymptote

Vertikale Asymptote:

Schiefe Asymptote:

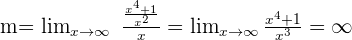
Es gibt also keine.

Monotonieverhalten

Wir stellen fest, dass

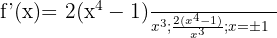
und somit

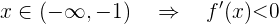
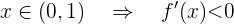
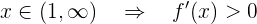
Die Funktion steigt also im Intervall und fällt im Intervall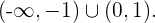

Außerdem sind die Tiefpunkte gegeben durch und

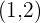
Konkavität und Konvexität

Wir stellen fest, dass

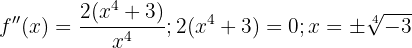
und somit

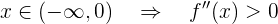
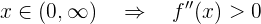
Daraus folgern wir, dass die Funktion konkav ist im Intervall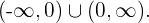

Wendepunkte

Es gibt keinen Wendepunkt.

Grafische Darstellung

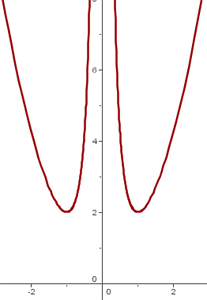
Definitionsbereich: Wir eliminieren den Punkt, an dem der Nenner 0 wird
Symmetrie: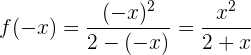. Es liegt keine Symmetrie vor.
Schnittpunkte mit den AchsenSchnittpunkt mit der -Achse:

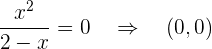
Schnittpunkt mit der -Achse:

Asymptoten

Horizontale Asymptote:

Wir stellen fest, dass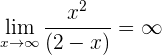

Somit gibt es keine horizontale Asymptote.

Vertikale Asymptote:

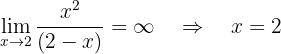
Schiefe Asymptote:

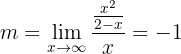
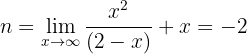
und somit

Monotonieverhalten

Wir ermitteln die kritischen Punkte

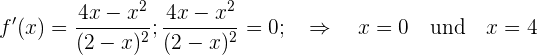
Wir untersuchen die Intervalle

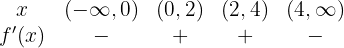
Das heißt, sie steigt im Intervall 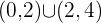und fällt im Intervall .

Wir untersuchen die kritischen Punkte, die wir mit der 2. Ableitung ermitteln, um die Minima und Maxima zu bestimmen.

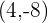ist ein Minimum und ein Maximum.

Konkavität und Konvexität

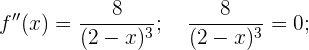
Da wir keine Lösung haben, unterteilen wir die Intervalle des Definitionsbereichs ausgehend von der 2, die nicht zum Definitionsbereich gehört.

Wir erhalten

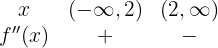
Sie ist im Intervall 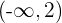konvex und im Intervall 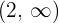konkav.

Wendepunkte:

Es gibt keinen Wendepunkt.

Grafische Darstellung

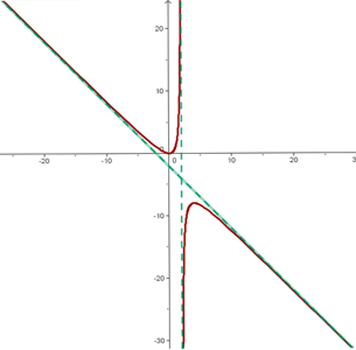
Definitionsbereich: Symmetrie: 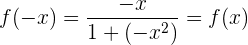Wir haben Symmetrie zum Ursprung, d.h. es ist eine ungerade Funktion.
Schnittpunkte mit den AchsenSchnittpunkt mit der -Achse:

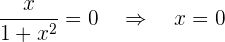
Der Schnittpunkt mit der Achse ist somit

Schnittpunkt mit der -Achse:

Wir haben

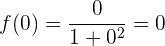
Somit ist der Schnittpunkt

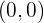
Asymptoten

Horizontale Asymptote:

Sie hat weder vertikale noch schiefe Asymptoten.

Monotonieverahalten

Wir bestimmen die kritischen Punkte

Nun überprüfen wir, welches Vorzeichen die Funktion hat, wenn wir den Definitionsbereich wie folgt unterteilen:

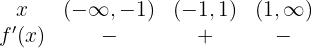
Daraus folgt, dass die Funktion im Intervall steigt und im Intervall fällt.

Wir untersuchen die kritischen Punkte der 2. Ableitung und erhalten

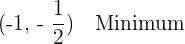
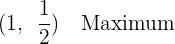
Konkavität und Konvexität

Wir berechnen die Punkte, an denen die 2. Ableitung 0 wird

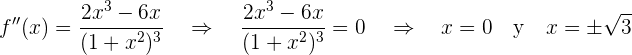
Wir überprüfen das Vorzeichen in den Intervallen

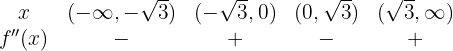
Die Funktion ist somit konvex im Intervall und konkav im Intervall .

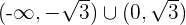Wendepunkte

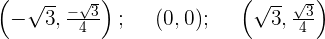
Grafische Darstellung

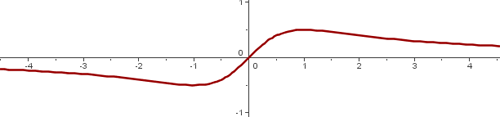
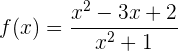
Definitionsbereich:
Symmetrie: 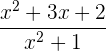. Es liegt keine Symmetrie vor.
Schnittpunkte mit den AchsenSchnittpunkte mit der -Achse:

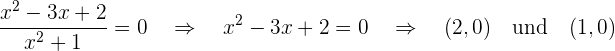
Schnittpunkt mit der -Achse:

Asymptoten

Horizontale Asymptote

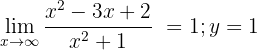
Sie hat weder vertikale noch schiefe Asymptoten.

Monotonieverhalten

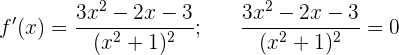
und somit

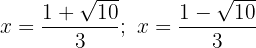
Nun überprüfen wir, welches Vorzeichen die Funktion hat, wenn wir den Definitionsbereich wie folgt unterteilen:

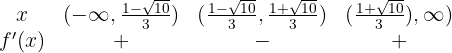
Sie steigt im Intervall 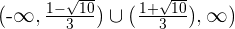und fällt im Intervall

Wir untersuchen die kritischen Punkte der 2. Ableitung und erhalten

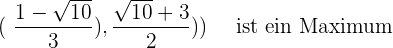
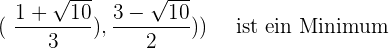
Wir stellen mit den erhaltenen Werten grafisch dar:

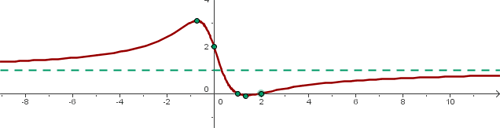
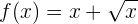
Definitionsbereich: Da wir die Wurzel aus "" berechnen müssen, gilt
Symmetrie: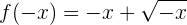
Es liegt keine Symmetrie vor.
Schnittpunkte mit den AchsenSchnittpunkte mit der -Achse:

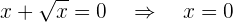
Der Schnittpunkt ist also

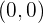
Schnittpunkt mit der -Achse:

Der Schnittpunkt ist also

Asymptoten

Es gibt keine Asymptoten.

Monotonieverhalten

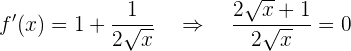
Die kritischen Punkte lauten also

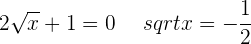
Da es keine Lösung gibt, sehen wir uns nur das Intervall des Definitionsbereichs an

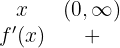
Die Funktion steigt.

Maxima und Minima

Es gibt keine lokalen Extremstellen.

Konkavität und Konvexität
Wir berechnen die 2. Ableitung und setzen gleich 0

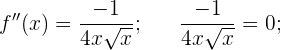
Da es keine Lösung gibt, nehmen wir das Intervall des Definitionsbereichs und erhalten

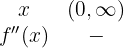
Die Funktion ist konkav.

Wendepunkte

Es gibt keinen Wendepunkt.

Grafische Darstellung

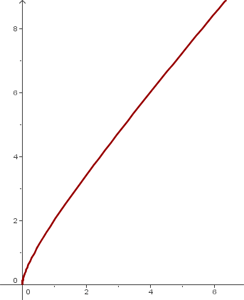
Definitionsbereich: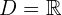
Symmetrie: 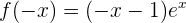. Es liegt keine Symmetrie vor.
Schnittpunkte mit den AchsenSchnittpunkt mit der -Achse:

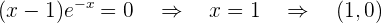
Schnittpunkt mit der -Achse:

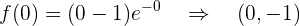
Asymptoten

Horizontale Asymptote:

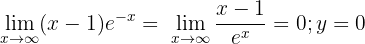
Es gibt weder vertikale noch schiefe Asymptoten.

Monotonieverhalten

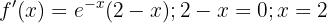
Wir untersuchen das Vorzeichen

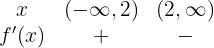
Daraus folgt, dass die Funktion bei 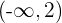steigt und bei 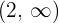fällt.

Wir untersuchen die kritischen Punkte der 2. Ableitung und erhalten

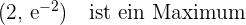
Konkavität und Konvexität

Wir berechnen die 2. Ableitung und bestimmen die Punkte, für die sie 0 wird

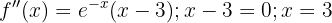
Wir unterteilen den Definitionsbereich in 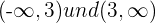und untersuchen das Vorzeichen der 2. Ableitung in diesen Intervallen

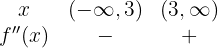
Die Funktion ist also konvex im Intervall und konkav im Intervall .

Wendepunkte

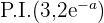
Grafische Darstellung

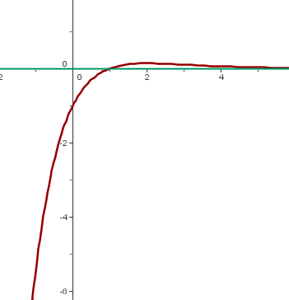
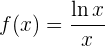
Definitionsbereich: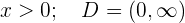
Symmetrie: . Es liegt keine Symmetrie vor.
Schnittpunkte mit den AchsenSchnittpunkte mit der -Achse:

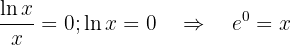
Das heißt,  und der Schnittpunkt wäre

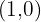
Schnittpunkt mit der -Achse:

Es gibt keinen Schnittpunkt mit der -Achse

Asymptoten

Horizontale Asymptote:

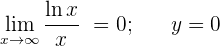
Vertikale Asymptoten:

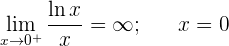
Monotonieverhalten
Wir berechnen die kritischen Punkte

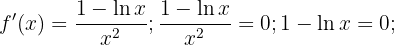
und erhalten den kritischen Punkt . Somit

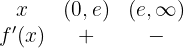
Die Funktion steigt bei 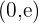und fällt bei . Ein Maximum ist bei .

Konkavität und Konvexität

Wir setzen die 2. Ableitung gleich 0

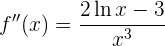
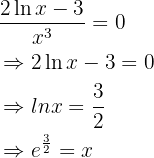
Wir unterteilen den Definitionsbereich und untersuchen das Vorzeichen der 2. Ableitung. Daraus folgt, dass die Funktion bei konvex ist und bei konkav ist.

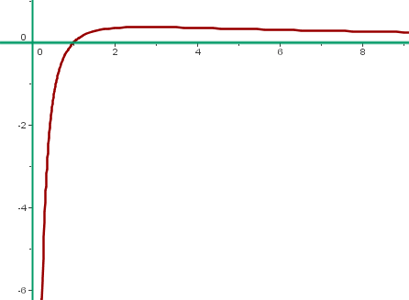
Grafische Darstellung