In diesem Abschnitt befassen wir uns mit Aufgaben zur Varianz. Wähle bei jeder Frage die Antwort aus, die die Varianz des gegebenen Datensatzes darstellt.
Die Anzahl der Male, die eine Gruppe von drei Freunden innerhalb einer Woche Pasta isst, beträgt 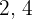 bzw.
bzw. 
Bitte wähle eine Antwort aus.
Zunächst berechnen wir den Mittelwert:
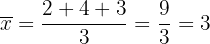
Und schließlich berechnen wir die Varianz:
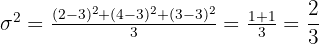
Eine Gruppe von vier Freunden trinkt täglich  Liter Wasser. Die Varianz dieses Datensatzes beträgt also:
Liter Wasser. Die Varianz dieses Datensatzes beträgt also:
Bitte wähle eine Antwort aus.
Zunächst berechnen wir den Mittelwert:
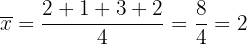
Und schließlich berechnen wir die Varianz:
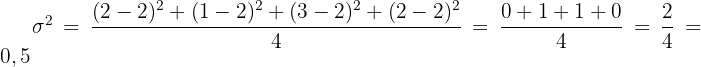
Die Anzahl der Stunden, die Carmen in der vergangenen Woche täglich ferngesehen hat, beträgt:  . Anhand des Datensatzes ergibt sich folgende Varianz:
. Anhand des Datensatzes ergibt sich folgende Varianz:
Bitte wähle eine Antwort aus.
Zunächst berechnen wir den Mittelwert:

Schließlich berechnen wir die Varianz:
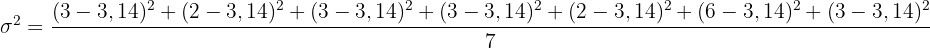

Die Anzahl der Male, die Maria sich eine Woche lang täglich die Zähne putzt: 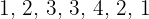 . Die Varianz dieses Datensatzes ist:
. Die Varianz dieses Datensatzes ist:
Bitte wähle eine Antwort aus.
Zunächst berechnen wir den Mittelwert:
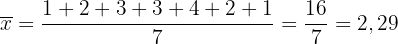
Schließlich berechnen wir die Varianz:
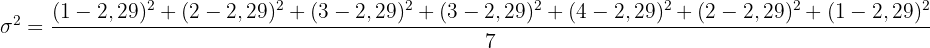
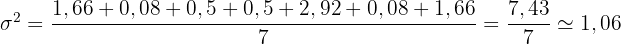
Die Noten der Mathematikprüfungen, die Paul während des Schuljahres geschrieben hat, sind . Die Varianz dieses Datensatzes ist:
. Die Varianz dieses Datensatzes ist:
Bitte wähle eine Antwort aus.
Zunächst berechnen wir den Mittelwert:
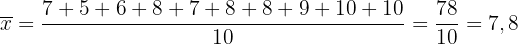
Schließlich berechnen wir die Varianz:
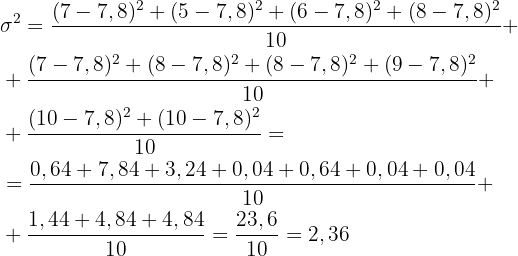
Die Anzahl der Stunden, die zehn Gruppen von Schüler*innen einer Klasse für eine Forschungsarbeit zum Thema Geometrie aufwenden, beträgt 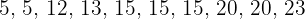 . Die Varianz dieses Datensatzes ist:
. Die Varianz dieses Datensatzes ist:
Bitte wähle eine Antwort aus.
Zunächst berechnen wir den Mittelwert:
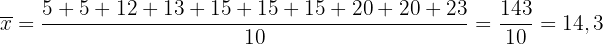 .
.
Und schließlich berechnen wir die Varianz:

Die Körpergröße in Zentimetern einer Gruppe von fünf Freunden beträgt 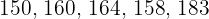 . Die Varianz dieses Datensatzes ist:
. Die Varianz dieses Datensatzes ist:
Bitte wähle eine Antwort aus.
Zunächst berechnen wir den Mittelwert:
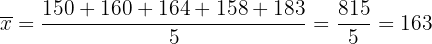
Und schließlich die Varianz:
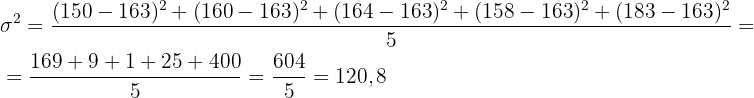
Die Anzahl der Kinobesuche pro Monat jedes einzelnen Mitglieds einer Gruppe von elf Freunden beträgt  . Die Varianz dieses Datensatzes ist:
. Die Varianz dieses Datensatzes ist:
Bitte wähle eine Antwort aus.
Wie in den vorherigen Aufgaben berechnen wir zunächst den Mittelwert und verwenden diesen dann, um die Varianz zu ermitteln:
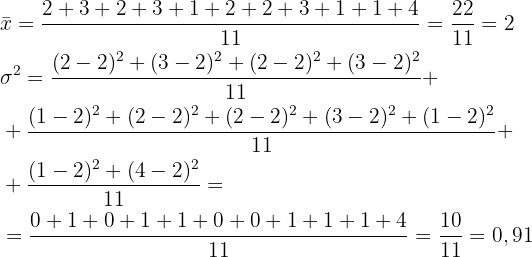
Beantworte die folgenden Fragen:
Die erzielten Punkte in Mathematik von 26 Schüler*innen einer Klasse sind  .
.
Berechne die Varianz der erzielten Punkte und runde gegebenenfalls auf zwei Dezimalstellen:
 =
=
Dieses Feld ist erforderlich.
Zunächst können wir die Daten unter Berücksichtigung der Werte ( ) und der Häufigkeit (
) und der Häufigkeit ( ), mit der sie auftreten, umschreiben, um anschließend ihre Produkte zu berechnen:
), mit der sie auftreten, umschreiben, um anschließend ihre Produkte zu berechnen:
| xi | fi | xi · fi | xi² · fi |
|---|---|---|---|
| 2 | 1 | 2 | 4 |
| 3 | 3 | 9 | 27 |
| 4 | 7 | 28 | 112 |
| 5 | 6 | 30 | 150 |
| 6 | 6 | 36 | 216 |
| 7 | 2 | 14 | 98 |
| 8 | 1 | 8 | 64 |
| Total | 26 | 127 | 671 |
Sobald wir die Summe aller  haben, berechnen wir den Mittelwert:
haben, berechnen wir den Mittelwert:
 .
.
Und schließlich berechnen wir die Varianz:
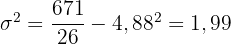 .
.
Die Fehltage von 25 Schüler*innen einer Klasse sind:  . Berechne die Varianz:
. Berechne die Varianz:
 =
=
Dieses Feld ist erforderlich.
Zunächst können wir die Daten in einer Tabelle unter Berücksichtigung der Werte ( ) und der Häufigkeit (
) und der Häufigkeit ( ), mit der sie auftreten, umschreiben, um anschließend ihre Produkte zu berechnen:
), mit der sie auftreten, umschreiben, um anschließend ihre Produkte zu berechnen:
| xi | fi | xi · fi | xi² · fi |
|---|---|---|---|
| 0 | 6 | 0 | 0 |
| 1 | 8 | 8 | 8 |
| 2 | 6 | 12 | 24 |
| 3 | 1 | 3 | 9 |
| 4 | 1 | 4 | 16 |
| 6 | 1 | 6 | 36 |
| 7 | 2 | 14 | 98 |
| Total | 25 | 47 | 191 |
Sobald wir die Summe aller  und die gesamten Daten haben, berechnen wir den Mittelwert:
und die gesamten Daten haben, berechnen wir den Mittelwert:
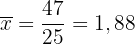 .
.
Schließlich berechnen wir die Varianz:
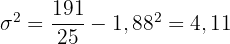 .
.
Mit KI zusammenfassen:


