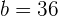Was ist das arithmetische Mittel?
In der Mathematik ist das arithmetische Mittel einer Reihe von reellen Zahlen die Summe der Werte geteilt durch die Anzahl der Werte. Wenn wir zum Beispiel die Durchschnittsnote der Schüler in einer Klasse wissen wollen, addieren wir zunächst die Noten aller Schüler in der Klasse und teilen sie dann durch die Anzahl der Schüler in der Klasse.
Aufgaben mit Lösungen zum arithmetischen Mittel
1 Beachte folgende Zahlen: 
und berechne:
a) Berechne den Mittelwert.
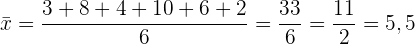
b) Wir multiplizieren die vorhergehenden Werte mit 
. Wie lautet der neue Mittelwert?
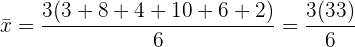
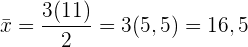
Wir stellen fest, dass, wenn alle Werte der Variablen mit multipliziert werden, das arithmetische Mittel mit multipliziert wird.
Diese Eigenschaft lässt sich in der folgenden Formel darstellen
mit der Konstante
2 Einer Zahlenreihe, die aus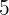 
Zahlen besteht und deren Mittelwert 
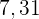ist, werden die Zahlen 
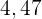und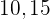 
hinzugefügt. Wie lautet der neue Mittelwert dieser Zahlenfolge?
Wir wissen bereits Folgendes:
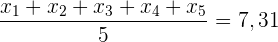
Wir berechnen nun den Mittelwert der Zahlen wie folgt
Dies bedeutet, dass der Mittelwert der sieben Zahlen berechnet werden kann, wenn der Mittelwert der ersten fünf Zahlen bekannt ist
3 Berechne den Mittelwert einer statistischen Verteilung, die durch folgende Tabelle gegeben ist:
| xi | 61 | 64 | 67 | 70 | 73 |
|---|---|---|---|---|---|
| fi | 5 | 18 | 42 | 27 | 8 |
In der Tabelle sind die Variable 
und die Anzahl ihrer Wiederholungen im Datensatz 
angegeben, weshalb die Tabelle mit dem Produkt aus der Variablen und ihrer absoluten Häufigkeit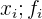 
ergänzt werden muss, um die Summe aller Werte , die Mal wiederholt werden, zu erhalten. So können wir sie schließlich alle addieren und sie durch die Anzahl der erhaltenen Werte teilen. Wir sehen uns folgende Formel an:
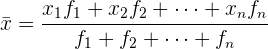
Die Tabelle sieht wie folgt aus
| xi | fi | xi · fi |
|---|---|---|
| 61 | 5 | 305 |
| 64 | 18 | 1152 |
| 67 | 42 | 2814 |
| 71 | 27 | 1890 |
| 73 | 8 | 584 |
| 100 | 6745 |
Nun müssen wir nur noch die Division durchführen
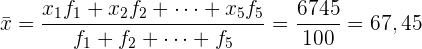
und erhalten das gewünschte Ergebnis.
4 Bestimme den Mittelwert der statistischen Verteilung, die durch folgende Tabelle gegeben ist:
| fi | |
|---|---|
| [10, 15) | 3 |
| [15, 20) | 5 |
| [20, 25) | 7 |
| [25, 30) | 4 |
| [30, 35) | 8 |
Zunächst einmal ist zu beachten, dass die Werte jetzt nicht mehr auf die gleiche Weise dargestellt werden wie zuvor, sondern dass wir Werteintervalle haben. In diesem Fall berechnen wir die sogenannte Klassenmitte 
. Hierzu ermitteln wir den Mittelwert zweier Werte, die das Intervall definieren. Zum Beispiel:
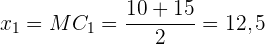
So verfahren wir auch mit den anderen Intervallen.
Sobald wir mit der Berechnung fertig sind, vervollständigen wir die Tabelle mit dem Produkt aus der Variable und ihrer absoluten Häufigkeit 
, um den Mittelwert zu berechnen
| xi | fi | xi · fi | |
|---|---|---|---|
| [10, 15) | 12,5 | 3 | 37,5 |
| [15, 20) | 17,5 | 5 | 87,5 |
| [20, 25) | 22,5 | 7 | 157,5 |
| [25, 30) | 27,5 | 4 | 110 |
| [30, 35) | 32,5 | 2 | 65 |
| 21 | 457,5 |
Wir berechnen die Summe der Produkte aus Variable und absoluter Häufigkeit , die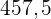 
ist , und dividieren diese durch die Gesamtwerte 
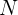, die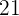 
sind.
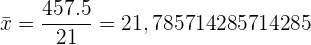
5 Berechne den Mittelwert der statistischen Verteilung:
| fi | |
|---|---|
| [0, 5) | 3 |
| [5, 10) | 5 |
| [10, 15) | 7 |
| [15, 20) | 8 |
| [20, 25) | 2 |
| [25, ∞) | 6 |
Wir berechnen als Erstes 
| xi | fi | |
|---|---|---|
| [0, 5) | 2,5 | 3 |
| [5, 10) | 7,5 | 5 |
| [10, 15) | 12,5 | 7 |
| [15, 20) | 17,5 | 8 |
| [20, 25) | 22,5 | 2 |
| [25, ∞) | --- | 6 |
| 31 |
Wir sehen, dass wir den Mittelwert NICHT berechnen können, da wir die Klassenmitte des letzten Intervalls nicht bestimmen können.
6 Ein Würfel wird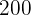 
Mal geworfen. Die Ergebnisse werden in folgender Tabelle dargestellt:
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| fi | a | 32 | 35 | 33 | b | 35 |
Bestimme und
. Der Durchschnittswert liegt bei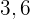 
.
| xi | fi | xi · fi |
|---|---|---|
| 1 | a | a |
| 2 | 32 | 64 |
| 3 | 35 | 125 |
| 4 | 33 | 132 |
| 5 | b | 5b |
| 6 | 35 | 210 |
| 135 + a + b | 511 + a + 5b |
Wir nehmen die Gesamtsumme der Daten und setzen sie gleich der Gesamtmenge der bekannten Daten
Das bedeutet:
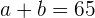
Wir haben unsere erste Gleichung.
Nun berechnen wir den Mittelwert der Verteilung und setzen ihn mit dem gegebenen Wert gleich
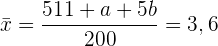
Wir bringen die Gleichung in folgende Form
und erhalten so folgendes Gleichungssystem
Dieses können wir wie folgt lösen
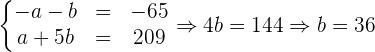
und somit
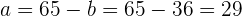
Ergebnis:
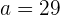und 
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
