Kapitel
Definition
Der Mittelwert ist der Wert, den man erhält, wenn man alle Daten einer Datenreihe summiert und durch die Gesamtzahl der Daten teilt. Der Mittelwert wird durch das Zeichen 
dargestellt und auf folgende Weise berechnet:
wobei jedes 
für einen unserer Werte der Datenreihe steht und 
für die Gesamtzahl der vorliegenden Daten.
Beispiel:
Sechs unserer Freunde haben folgendes Körpergewicht: 
und 
.
Ermittle das durchschnittliche Gewicht.
Wir verfügen über sechs Daten, das heißt 
. Berechne nun den Mittelwert
Arithmetisches Mittel für gruppierte Daten
Wenn gruppierte Daten in einer Häufigkeitstabelle vorliegen, wird der Mittelwert etwas anders dargestellt:
media es distinta. Nehmen wir an, wir verfügen über 
unterschiedliche Klassen in unserer Häufigkeitstabelle, wobei für jede Klasse 
der entsprechende Mittelwert und die entsprechende Häufigkeit 
vorliegen. Das arithmetische Mittel wird dann wie folgt berechnet
Man bemerke, dass nun die Summe aller Häufigkeiten jeder Klasse ist, also
.
Wenn außerdem jede Gruppe bzw. Klasse ein Intervall darstellt, ist der Mittelwert dieses Intervalls einfach der Mittelpunkt zwischen den beiden Grenzwerten, das heißt, wenn eine Gruppe das Intervall 
darstellt, ist ihr Mittelwert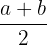 
.
Nebenbemerkung: beim Gruppieren der Daten einer Häufigkeitstabelle ersetzt man jeden Wert mit dem Mittelwert der Gruppe bzw. Klasse, zu der er gehört. Die Summe aller Häufigkeiten ist gleich der Datenmenge, die wir erhalten würden, wenn wir keine Gruppierung vernehmen würden. Was wir daher eigentlich tun, wenn wir den Mittelwert gruppierter Daten berechnen, ist, jeden Wert durch den Mittelwert der Gruppe bzw. Klasse zu ersetzen, zu der er gehört. Wenn ungruppierte Daten vorliegen ist es besser, diese nicht zu gruppieren, da dies immer mit einem Datenverlust einhergeht.
Übungen zur Berechnung des Mittelwerts für gruppierte Daten
In einem Test, an dem eine Gruppe von 42 Personen teilnahm, wurden folgende Punktzahlen erzielt
Ermittle die durchschnittliche Punktzahl.
| | |
|---|---|---|
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  | |
 |  |  |
 |  |  |
Man kann sehen, dass jedes den Mittelpunkt des zugehörigen Intervalls darstellt.
Um den Mittelwert zu berechnen, ermittelt man zuerst die Summer der 
. Dann erstellt man eine neue Spalte und trägt dort die Produkte der Variablen mit der zugehörigen absoluten Häufigkeit ein und summiert alles. Ebenso muss als Summe der absoluten Häufigkeiten berechnet werden.
| | | |
|---|---|---|---|
| | | |
| | |  |
| | |  |
| | |  |
| | |  |
| | |  |
| | |  |
| Summen: |  |  |
Der Mittelwert unserer Daten ist folglich:
Eigenschaften des arithmetischen Mittels
sei eine Datenmenge und der Mittelwert der Daten. Die Abweichung eines Werts der Datenreihe vom Mittelwert wird wie folgt definiert:
.
1. Die Summe der Abweichungen aller Daten einer Häufigkeitsverteilung
zum Mittelwert derselben ist gleich Null. Das heißt
Die Summe der Abweichungen der Zahlen 
von ihrem arithmetischen Mittel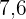 
ist gleich 
:
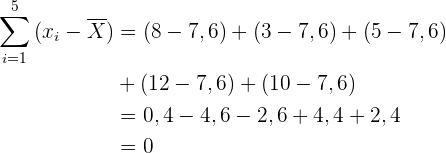
2. Die Summe der Quadrate der Abweichungen der Werte der Variablen in Bezug auf eine beliebige Zahl wird minimal, wenn diese Zahl mit dem arithmetischen Mittel übereinstimmt. In anderen Worten: die folgende Formel wird immer erfüllt
Wenn 
3. Wenn zu allen Werten der Variablen dieselbe Zahl addiert wird, ist auch der neue Mittelwert um dieselbe Zahl höher als zuvor. Das heißt, angenommen wir verfügen über die Daten 
mit Mittelwert und addieren zu allen Daten eine Zahl 
, 
, so ist der Mittelwert der neuen Daten
4. Wenn alle Werte der Variablen mit derselben Zahl multipliziert werden,
multipliziert sich auch der Mittelwert mit dieser Zahl. Angenommen, wir verfügen über die Daten mit Mittelwert und multiplizieren alle Daten mit einer Zahl , 
, so ist der neue Mittelwert der Daten
Beobachtungen zum arithmetischen Mittel
1. Der Mittelwert kann ausschließlich für quantitative Variablen ermittelt werden.
2. Der Mittelwert ist unabhängig von der Intervallbreite.
3. Mittelwerte sind sehr empfindlich gegenüber Extremwerten, die auch als Ausreißer bezeichnet werden. Bei folgender Verteilung von Körpergewichten
.
ist der Mittelwert 
wenig repräsentativ
bezüglich der Verteilung, da ein Wert der Datenmenge sehr weit entfernt von allen anderen liegt, nämlich 
.
4. Der Mittelwert kann nicht berechnet werden, wenn ein Intervall mit einer unbestimmten Breite vorliegt.
| | |
|---|---|---|
 |  |  |
 |  |  |
 |  | |
 |  |  |
 | | |
 |
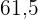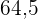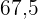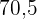In diesem Fall ist es nicht möglich, den Mittelwert zu bestimmen, da die Klasse
des letzten Intervalls nicht berechnet werden kann.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
