Kapitel
Die Varianz gibt die Abweichungen der Werte einer statistischen Verteilung vom Mittelwert an.
Die Varianz wird berechnet, indem man das Quadrat der Standardabweichung bildet.
Dargestellt wird sie mit dem Zeichen: 
.
Die Formel zur Berechnung der Varianz lautet:
Beispiele zur Berechnung der Varianz
1 Berechne die Varianz der Verteilung: 
Berechne den Mittelwert
Berechne die Varianz
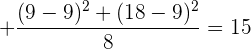
2 Berechne die Varianz der Verteilung: 
Berechne den Mittelwert
Berechne die Varianz
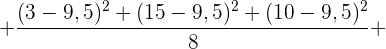
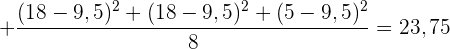
3 Berechne die Varianz der Verteilung: 
Entsprechend der vorherigen Aufgaben wird zuerst der Mittelwert berechnet, um dann die Varianz zu ermitteln.
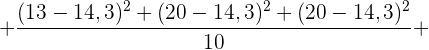
4 Berechne die Varianz der Verteilung: 
Entsprechend der vorherigen Aufgaben wird zuerst der Mittelwert berechnet, um dann die Varianz zu ermitteln.
5 Berechne die Varianz der Verteilung: 
Entsprechend der vorherigen Aufgaben wird zuerst der Mittelwert berechnet, um dann die Varianz zu ermitteln.
Varianz für gruppierte Daten
Um die Berechnung der Varianz zu vereinfachen, verwenden wir folgende Ausdrücke (entsprechend der vorherigen Aufgaben)
Beispiele zur Berechnung der Varianz für gruppierte Daten
Berechne die Varianz der folgenden Verteilung:
 |  |  |  | |
|---|---|---|---|---|
 |  |  | |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  | |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |
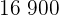Die Spalte wurde eingefügt, um ihre Summe 
zu ermitteln, die
anschließend durch 
geteilt wird, um den Mittelwert zu erhalten
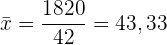
Die Spalte wurde hinzugefügt, da wir ihre Summe 
zu ermitteln, die anschließend durch geteilt wird. Vom Ergebnis ziehen wir den Mittelwert zum Quadrat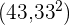 
ab.
Eigenschaften der Varianz
1 Für gleiche Werte ist die Varianz immer positiv oder gleich Null.
2 Wenn zu allen Daten dieselbe Zahl addiert wird, bleibt die Varianz dieselbe.
3 Wenn alle Werte der Variablen mit einer Zahl multipliziert werden, multipliziert sich die Varianz um die Zahl zum Quadrat.
4 Wenn mehrere Verteilungen mit demselben Mittelwert vorliegen und ihre entsprechenden Varianzen bekannt sind, kann die Gesamtvarianz ermittelt werden.
Wenn alle Werte der Datenmenge gleich groß sind, gilt:
Wenn die Werte der Datenmenge unterschiedlich groß sind, gilt:
Anmerkungen zur Varianz
1 Die Varianz ist, wie der Mittelwert, sehr empfindlich gegenüber Extremwerten.
2 Wenn kein Mittelwert berechnet werden kann, kann auch die Varianz nicht ermittelt werden.
3 Die Varianz wird nicht in der selben Einheit wie die Daten ausgedrückt, da die Abweichungen quadriert sind.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
