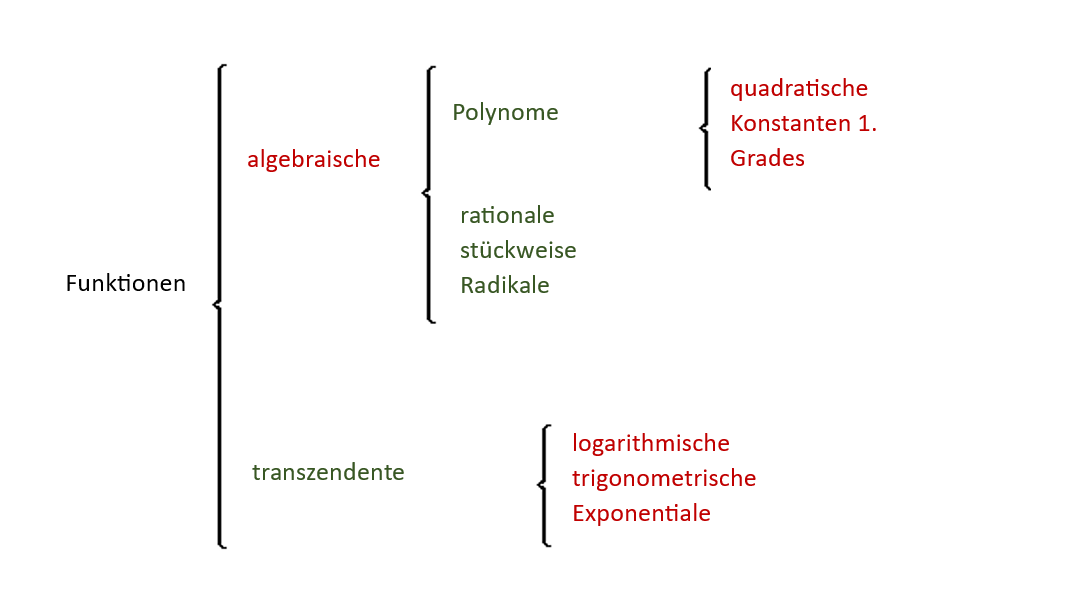
Algebraische Funktionen
Bei algebraischen Funktionen sind folgende Rechenoperationen mit der unabhängigen Variable auszuführen: die Addition, die Subtraktion, die Multiplikation, die Division, das Potenzieren und das Radizieren.
Algebraische Funktionen können sein:
Explizit dargestellte Funktionen
Die Abbildungen von 
werden durch einfache Substitution wie in diesem Beispiel ermittelt : 
Implizit dargestellte Funktionen
Die Abbildungen von können nicht durch einfache Substitution wie in diesem Beispiel ermittelt werden: 
Neben dieser Einteilung gibt es noch 6 weitere Typen algebraischer Funktionen
1 Polynomfunktionen
- Diese Funktionen bestehen aus einem Polynom.
- Ihre Definitionsmenge ist
, also eine reelle Zahl.
2 Konstante Funktionen
- Der Funktionswert ist durch eine reelle Zahl gegeben.
- Grafisch dargestellt ist die konstante Funktion eine horizontale Gerade, die parallel zur x-Achse verläuft.
3 Polynomfunktionen 1. Grades
1
- Grafisch dargestellt ist diese Funktion eine schräge Gerade, die durch 2 Punkte der Funktion definiert ist.
- Funktionen von diesem Typ sind:
- Affine Funktion
2 
- Lineare Funktion
3 
- Identische Abbildung
4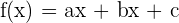 
- Quadratische Funktionen
- Dies sind Polynomfunktionen 2. Grades
- Grafisch dargestellt ergibt sich hierfür eine Parabel.
4 Rationale Funktionen
- Die Definitionsmenge bilden alle reellen Zahlen außer den Werten von x, für die der Nenner null wird.
- Der Funktionswert ist durch den Quotienten aus Polynomen gegeben:
5 Wurzelfunktionen
- Der Funktionswert ist durch die Variable x unter dem Wurzelzeichen gegeben.
- Die Definitionsmenge einer Wurzelfunktion mit einem ungeraden Wurzelexponenten ist .
- Die Definitionsmenge einer Wurzelfunktion mit einem geraden Wurzelexponenten bilden alle Werte, für die der Radikand größer oder gleich null ist.
6 Abschnittsweise definierte Funktionen
Es handelt sich um Funktionen, die je nach den betrachteten Intervallen durch unterschiedliche Kriterien definiert sind.
Betragsfunktion
Abrundungsfunktion und Aufrundungsfunktion
Mantissenfunktion
Signumfunktion
Transzendente Funktionen
Dies sind verschiedene Funktionen, die weder Polynom- noch Wurzelfunktionen sind. Folgende Funktionen sind transzendent:
1 Exponentialfunktionen
a ist hierbei eine positive reelle Zahl. Bei der Exponentialfunktion ist der Exponent eine Variable.
2 Logarithmusfunktionen
Die Logarithmusfunktion zur Basis a ist die Umkehrfunktion der Exponentialfunktion zur Basis a.
3 Trigonometrische Funktionen
Sinusfunktion
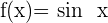
Kosinusfunktion
Tangensfunktion
Kosekansfunktion
Sekansfunktion
Kotangensfunktion
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
