Kapitel

Grenzwert eines Punktes
Wenn  eine gewöhnliche Funktion ist (polynomisch, rational, exponentiell, logarithmisch usw.) und im Punkt
eine gewöhnliche Funktion ist (polynomisch, rational, exponentiell, logarithmisch usw.) und im Punkt  definiert ist, dann gilt:
definiert ist, dann gilt: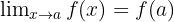
Das heißt: Um den Grenzwert zu berechnen, wird der Wert in die Funktion eingesetzt, gegen den die  -Werte konvergieren.
-Werte konvergieren.
Grenzwert einer abschnittsweise definierten Funktion
Um den Grenzwert einer abschnittsweise definierten Funktion zu untersuchen, müssen wir zunächst die seitlichen Grenzwerte an den Verbindungspunkten der verschiedenen Abschnitte untersuchen. Anschließend:
- wenn diese übereinstimmen, ist dies der Wert des Grenzwerts,
- wenn sie nicht übereinstimmen, existiert der Grenzwert nicht.
Ein Beispiel für eine abschnittsweise definierte Funktion, bei der die Grenzwerte nicht übereinstimmen, ist die ganzzahlige Funktion von  , bei der die Grenzwerte bei den ganzen Zahlen nicht übereinstimmen:
, bei der die Grenzwerte bei den ganzen Zahlen nicht übereinstimmen:
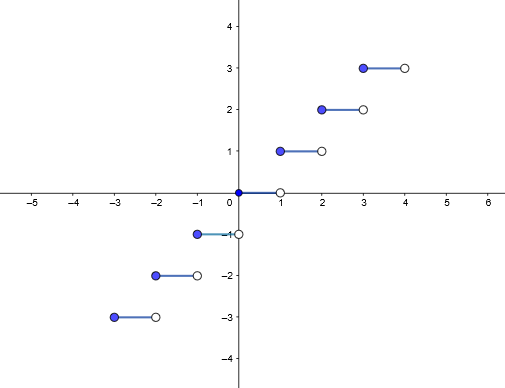
Ein Beispiel für eine Funktion, bei der die seitlichen Grenzwerte übereinstimmen, ist die folgende
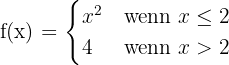
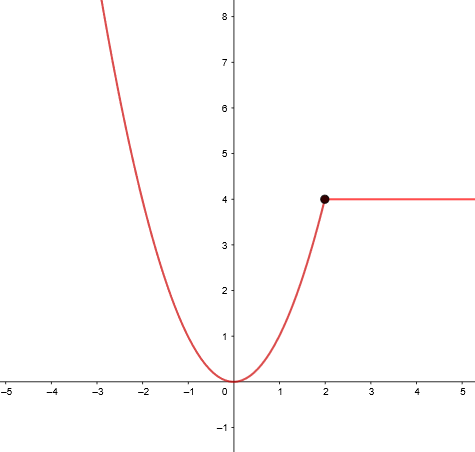
Grenzwert, wenn x gegen unendlich konvergiert
Um den Grenzwert einer Funktion zu berechnen, wenn  , werden die
, werden die  durch
durch  ersetzt.
ersetzt.
Polynomfunktionen im Unendlichen
Der Grenzwert einer Polynomfunktion, wenn  , ist
, ist  , je nachdem, ob der Term höchsten Grades positiv oder negativ ist.
, je nachdem, ob der Term höchsten Grades positiv oder negativ ist.
Zum Beispiel:
1 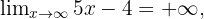
2 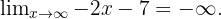
Umkehrfunktion eines Polynoms im Unendlichen
Wenn  ein Polynom beliebigen Grades ist, gilt:
ein Polynom beliebigen Grades ist, gilt:
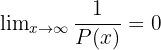
wenn  eine Konstante ist
eine Konstante ist
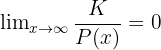
Grenzwert, wenn  gegen minus unendlich konvergiert
gegen minus unendlich konvergiert
Wenn 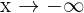 , gilt
, gilt
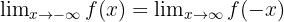
Wir wenden dies auf einige Polynomfunktionen an
1 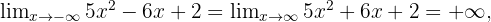
2 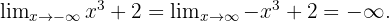
Grenzwert einer Exponentialfunktion
Wenn 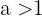 ,
,
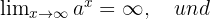
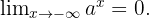
Wenn 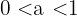 ,
,
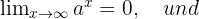
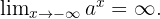
Grenzwert einer Logarithmusfunktion
Wenn 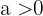 ,
,
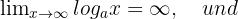
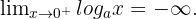
Wenn 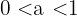 ,
,
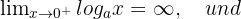
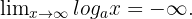
Mit KI zusammenfassen:












