Kapitel
Eine gemischte Zahl oder ein gemischter Bruch ist ein Ausdruck, der sich aus einem ganzzahligen Teil und einem Bruchteil zusammensetzt.
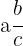
In diesem Ausdruck ist 
der ganzzahlige Teil, während 
der Bruchteil ist.
Einige weitere Beispiele sind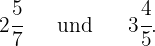
Äquivalenz zwischen gemischten Zahlen und unechten Brüchen
Zur Erinnerung: Eine gemischte Zahl ist einfach ein Ausdruck, der sich aus einem ganzzahligen Teil und einem Bruchteil zusammensetzt, aber das ist nicht die einzige Darstellungsform.
Eine andere Möglichkeit, eine gemischte Zahl darzustellen, ist ein unechter Bruch; unechte Brüche sind solche, bei denen der Nenner deutlich kleiner ist als der Zähler.
Im Folgenden beschreiben wir eine Methode, um den äquivalenten Ausdruck zwischen einer gegebenen gemischten Zahl und einem unechten Bruch zu finden.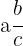 sei eine gemischte Zahl. Zunächst müssen wir den ganzzahligen Teil der gemischten Zahl durch die folgende Berechnung in einen Bruch umwandeln:
Wir stellen fest, dass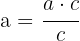 
und somit
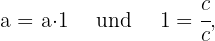
also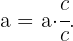
Nachdem wir nun den ganzzahligen Teil in einen Bruch umgewandelt haben, addieren wir ihn zum Bruchteil der gemischten Zahl, d. h. wir addieren wie folgt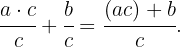
Der letztgenannte Ausdruck ist der unechte Bruch, der der ursprünglichen gemischten Zahl entspricht.
Für die gemischte Zahl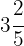 
ergeben sich zum Beispiel folgende Berechnungen.
Wir erinnern uns daran, dass wir zunächst den ganzzahligen Teil in einen unechten Bruch umwandeln müssen.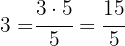
Dann addieren wir das Ergebnis der Umwandlung des ganzzahligen Teils mit dem Bruchteil, den wir bereits hatten. Dies ist
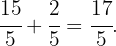
Die gemischte Zahl 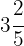ist als unechter Bruch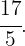 
Äquivalenz zwischen unechten Brüchen und gemischten Zahlen
Da wir einen unechten Bruch gefunden haben, der äquivalent zu einer gemischten Zahl ist, können wir dies auch umgekehrt durchführen. Das heißt, dass man für einen unechten Bruch eine äquivalente gemischte Zahl ermittelt; das Verfahren wird im Folgenden beschrieben.
sei ein unechter Bruch. Das bedeutet, dass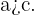 
Der erste Schritt besteht darin, die Division 
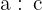durchzuführen. Aus dieser Division erhalten wir den ganzzahligen Teil 
und den Rest 
, um die gemischte Zahl wie folgt zu bilden
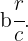
Wir führen die Berechnungen für diese Umrechnung am Beispiel des folgenden unechten Bruchs durch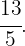 
In diesem Fall ist der ganzzahlige Teil, den wir aus der Division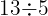 
erhalten, 
und der Rest ist 
weshalb
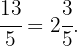
Rechnen mit gemischten Zahlen
Um mit gemischten Zahlen zu rechnen, werden diese in unechte Brüche umgewandelt und dann die angegebenen Rechenoperationen zwischen den Brüchen durchgeführt.
Unser erstes Beispiel ist 
Zunächst wandeln wir wie folgt um:
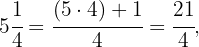
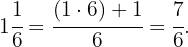
Zuletzt addieren wir die unechten Brüche
Als letztes Beispiel berechnen wir das Ergebnis von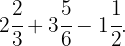 
Auch hier berechnen wir in einem ersten Schritt die unechten Brüche, die diesen gemischten Zahlen entsprechen.
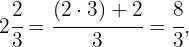
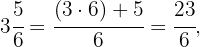
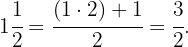
Und schließlich
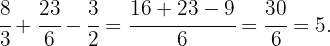
Aufgaben zu Brüchen
Wandle die folgenden gemischten Zahlen in Brüche um. Vereinfache, wenn nötig.
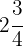
Zunächst müssen wir den ganzzahligen Teil durch folgende Berechnungen in einen unechten Bruch umwandeln: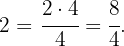 
Danach addieren wir dieses Ergebnis mit dem Bruchteil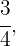 
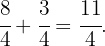
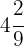
Zunächst müssen wir den ganzzahligen Teil durch folgende Berechnungen in einen unechten Bruch umwandeln: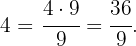 
Danach addieren wir dieses Ergebnis mit dem Bruchteil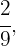 
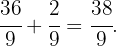
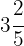
Zunächst müssen wir den ganzzahligen Teil durch folgende Berechnungen in einen unechten Bruch umwandeln: 
Danach addieren wir dieses Ergebnis mit dem Bruchteil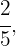 
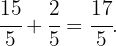
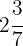
Zunächst müssen wir den ganzzahligen Teil durch folgende Berechnungen in einen unechten Bruch umwandeln: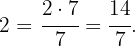 
Danach addieren wir dieses Ergebnis mit dem Bruchteil 
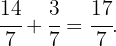
Drücke die folgenden Brüche als gemischte Zahlen aus
Wir beginnen mit der Division von 
durch 
. Das Ergebnis ist die ganze Zahl 
Da 
, bedeutet dies, dass der Rest der obigen Division 1 ist und der ganzzahlige Teil 2, wie wir bereits festgestellt haben. Daher lautet der Ausdruck als gemischte Zahl wie folgt
Wir beginnen mit der Division von 
durch 
. Das Ergebnis ist die ganze Zahl 
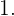Da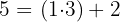 
, bedeutet dies, dass der Rest der obigen Division 2 ist und der ganzzahlige Teil 1, wie wir bereits festgestellt haben. Daher lautet der Ausdruck als gemischte Zahl wie folgt
Wir beginnen mit der Division von 
durch . Das Ergebnis ist die ganze Zahl 
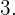Da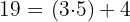 
, bedeutet dies, dass der Rest der obigen Division 4 ist und der ganzzahlige Teil 3, wie wir bereits festgestellt haben. Daher lautet der Ausdruck als gemischte Zahl wie folgt
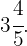
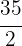
Wir beginnen mit der Division von 
durch . Das Ergebnis ist die ganze Zahl 
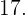Da 
, bedeutet dies, dass der Rest der obigen Division 1 ist und der ganzzahlige Teil 17, wie wir bereits festgestellt haben. Daher lautet der Ausdruck als gemischte Zahl wie folgt
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
