
Bestimme die Ellipsengleichung
Bevor wir die Aufgaben lösen, kannst du dir die Zusammenfassung über die Eigenschaften der Ellipse und ihre Gleichung ansehen.
Bestimme die Gleichung des geometrischen Ortes der Punkte  , deren Summe der Abstände zu den Fixpunkten
, deren Summe der Abstände zu den Fixpunkten  und
und  gleich
gleich  ist.
ist.
Es muss gelten, dass die Summe der Abstände  und
und  immer
immer  ist. Das heißt:
ist. Das heißt:

Wir erhalten also

Wir stellen die Gleichung um

Schließlich quadrieren wir und erhalten

Wir stellen fest, dass der Term  auf beiden Seiten der Gleichung steht. Daher können wir ihn kürzen und es bleibt
auf beiden Seiten der Gleichung steht. Daher können wir ihn kürzen und es bleibt

Wir lösen die Binome zum Quadrat und erhalten

Wenn wir gleichartige Terme  durch Division der Gleichung durch
durch Division der Gleichung durch  — umgruppieren, erhalten wir
— umgruppieren, erhalten wir

Wir haben bereits eine Wurzel beseitigt. Um die andere loszuwerden, wiederholen wir den Vorgang. Wir quadrieren den Ausdruck, lösen die Binome und stellen Terme um:

Das heißt:

Bestimme die Gleichung der Ellipse mit dem Brennpunkt , dem Scheitelpunkt
, dem Scheitelpunkt  und dem Mittelpunkt
und dem Mittelpunkt  .
.
Wir wissen, dass die große Halbachse der Abstannd zwischen dem Mittelpunkt  und dem Scheitelpunkt
und dem Scheitelpunkt  ist. Das heißt:
ist. Das heißt:

Außerdem ist die halbe Brennweite die Distanz zwischen dem Mittelpunkt  und dem Brennpunkt
und dem Brennpunkt  der Ellipse — also die Hälfte der Distanz zwischen den zwei Brennpunkten — das heißt,
der Ellipse — also die Hälfte der Distanz zwischen den zwei Brennpunkten — das heißt,

Schließlich berechnen wir die kleine Halbachse

Die Mittelpunktsgleichung der Ellipse ist also gegeben durch:

Bestimme die Ellipsengleichung mit folgenden Informationen:


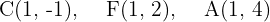
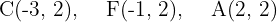

Wir zeigen dir die Berechnung mit den ersten gegebenen Punkten im Detail.
Wir wissen, dass die große Halbachse die Distanz zwischen dem Mittelpunkt  und dem Scheitelpunkt
und dem Scheitelpunkt  ist, also
ist, also

Außerdem ist die halbe Brennweite der Abstand zwischen dem Mittelpunkt  und dem Brennpunkt
und dem Brennpunkt  der Ellipse — also die Hälfte des Abstands zwischen den zwei Brennpunkten — das heißt:
der Ellipse — also die Hälfte des Abstands zwischen den zwei Brennpunkten — das heißt:
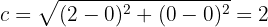
Schließlich berechnen wir die kleine Halbachse
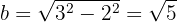
Die Mittelpunktsgleichung der Ellipse ist:


Wir erhalten

Die kleine Halbachse ist somit gegeben durch
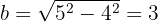
Die Mittelpunktsgleichung der Ellipse ist:

In diesem Fall dividieren wir  durch
durch  anstatt
anstatt 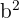 . Der Grund dafür ist, dass die Hauptachse vertikal verläuft (sowohl
. Der Grund dafür ist, dass die Hauptachse vertikal verläuft (sowohl  ,
,  und
und  haben den gleichen Wert für
haben den gleichen Wert für  ).
).
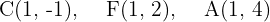
Die Hauptachse verläuft also vertikal:

Die kleine Halbachse ist somit gegeben durch
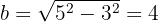
Die Mittelpunktsgleichung der Ellipse ist:

Wir beachten nun, dass die  -Koordinaten an jedem Punkt festgelegt sind. Die Hauptachse der Ellipse verläuft also horizontal.
-Koordinaten an jedem Punkt festgelegt sind. Die Hauptachse der Ellipse verläuft also horizontal.

Außerdem

Die Mittelpunktsgleichung der Ellipse ist

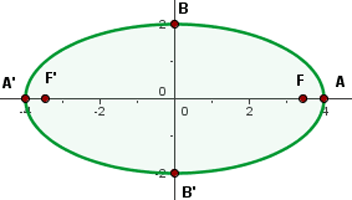
Bestimme die Mittelpunktsgleichung einer Ellipse, deren Hauptachse horizontal verläuft. Einer der Brennpunkte liegt  von einem Scheitelpunkt entfernt und
von einem Scheitelpunkt entfernt und  vom anderen Scheitelpunkt. Der Mittelpunkt befindet sich im Ursprung.
vom anderen Scheitelpunkt. Der Mittelpunkt befindet sich im Ursprung.
Sieh dir folgende Abbildung an:
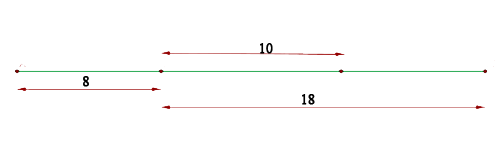
Wir wissen, dass die Brennweite 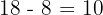 sein muss. Die halbe Brennweite ist also
sein muss. Die halbe Brennweite ist also
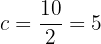
Das ist die Entfernung vom Mittelpunkt zu einem beliebigen Brennpunkt. Der Abstand zwischen dem Mittelpunkt und dem Scheitelpunkt beträgt somit
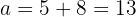
Somit erhalten wir
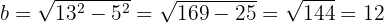
Die Ellipsengleichung lautet somit

Bestimme die Mittelpunktsgleichung einer Ellipse, die durch den Punkt  verläuft. Der Mittelpunkt liegt im Ursprung, die Hauptachse verläuft horizontal und die Exzentrizität ist
verläuft. Der Mittelpunkt liegt im Ursprung, die Hauptachse verläuft horizontal und die Exzentrizität ist  .
.
Die Ellipsengleichung muss folgende Form haben:
 ,
,
da sich der Mittelpunkt im Ursprung befindet. Außerdem verläuft die Ellipse durch den Punkt  . Es muss also gelten:
. Es muss also gelten:
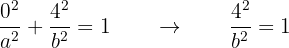
Wenn wir 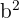 bestimmen, erhalten wir
bestimmen, erhalten wir 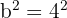 . Und da
. Und da 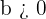 , folgt daraus
, folgt daraus

Darüber hinaus muss in der Formel für die Exzentrizität Folgendes erfüllt sein

Wenn wir die Gleichung quadrieren, ergibt sich
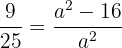
Wir multiplizieren die Gleichung mit  und im Anschluss mit
und im Anschluss mit  . Wir erhalten
. Wir erhalten
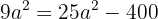
Wir fassen gleichartige Terme zusammen

Also ist  . Die Ellipsengleichung lautet
. Die Ellipsengleichung lautet

Schreibe die Mittelpunktsgleichung der Ellipse, deren Mittelpunkt im Ursprung liegt. Außerdem verläuft sie durch den Punkt  . Ihre Nebenachse misst
. Ihre Nebenachse misst  und verläuft vertikal.
und verläuft vertikal.
Da sich der Mittelpunkt der Ellipse im Ursprung befindet, muss ihre Gleichung folgende Form haben

Da die Nebenachse  misst, ist die kleine Halbachse
misst, ist die kleine Halbachse
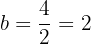
Da die Ellipse durch den Punkt  verläuft, muss die Gleichung Folgendes erfüllen
verläuft, muss die Gleichung Folgendes erfüllen
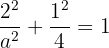
Wir bestimmen  und erhalten
und erhalten
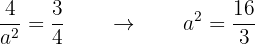
Das heißt

Die Ellipsengleichung lautet somit
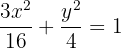
Die Brennweite einer Ellipse mit Mittelpunkt im Ursprung ist  und die Brennpunkte liegen auf der x-Achse. Ein Punkt der Ellipse ist von ihren Brennpunkten
und die Brennpunkte liegen auf der x-Achse. Ein Punkt der Ellipse ist von ihren Brennpunkten  bzw.
bzw.  entfernt. Berechne die Mittelpunktsgleichung dieser Ellipse.
entfernt. Berechne die Mittelpunktsgleichung dieser Ellipse.
Die Brennweite misst  . Die halbe Brennweite ist also
. Die halbe Brennweite ist also
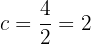
Ebenso ist die Summe der Abstände von jedem Punkt zu den Brennpunkten immer konstant. Dieser Abstand fällt mit der Hauptachse zusammen, so dass

Schließlich misst die kleine Halbachse
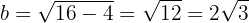
Die Ellipsengleichung lautet
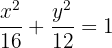
Bestimme die Gleichung der Ellipse, deren Mittelpunkt sich im Ursprung befindet. Die Brennpunkte liegen auf der x-Achse und sie verläuft durch die Punkte 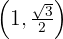 und
und 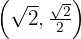 .
.
Da die Ellipse durch beide Punkte geht, muss sie das folgende Gleichungssystem erfüllen
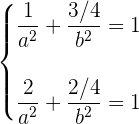
Dies ist ein nichtlineares Gleichungssystem mit zwei Unbekannten (der Link zeigt dir, wie du sie lösen kannst). In diesem Fall nehmen wir einen Variablentausch vor

Die Lösung dieses Systems ist

Um das zu überprüfen, kann du die Werte von  und
und  in das ursprüngliche Gleichungssystem einsetzen.
in das ursprüngliche Gleichungssystem einsetzen.
Die Ellipsengleichung lautet

Bestimme die Gleichung der Ellipse, deren Mittelpunkt sich im Ursprung befindet. Die Brennweite ist  , die Brennpunkte liegen auf der x-Achse und die Fläche des auf den Achsen konstruierten Rechtecks ist
, die Brennpunkte liegen auf der x-Achse und die Fläche des auf den Achsen konstruierten Rechtecks ist  .
.
Die Brennweite ist  . Somit
. Somit

Für die großen und kleinen Halbachsen gilt
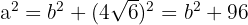
Auf der anderen Seite haben wir ein Rechteck, dessen Seiten  und
und  messen. Die Fläche ist gegeben durch
messen. Die Fläche ist gegeben durch

Daher müssen wir das folgende nichtlineare Gleichungssystem lösen:
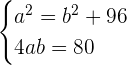
Dieses nichtlineare System kann gelöst werden, indem man die zweite Gleichung nimmt und ihren Wert in die erste Gleichung einsetzt. Dies ergibt eine biquadratische Gleichung. Die Lösung des Systems ist gegeben durch
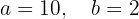
Die Ellipsengleichung lautet somit

Elemente anhand der Gleichung bestimmen
Ermittle die charakteristischen Elemente und die Mittelpunktsgleichung der Ellipse mit den Brennpunkten:  und
und 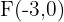 . Die Hauptachse misst
. Die Hauptachse misst  .
.
Ermittle die charakteristischen Elemente und die Mittelpunktsgleichung der Ellipse mit den Brennpunkten:  und
und 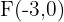 . Die Hauptachse misst
. Die Hauptachse misst  .
.
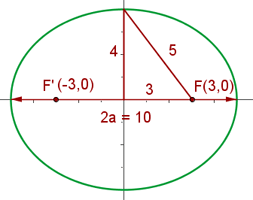
Große Halbachse:
Wir haben 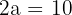 , weshalb die große Halbachse
, weshalb die große Halbachse  ist.
ist.
Halbe Brennweite:
Der Abstand zwischen den zwei Brennpunkten ist 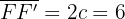 . Deshalb ist die halbe Brennweite
. Deshalb ist die halbe Brennweite  .
.
Kleine Halbachse:
Wir haben  , wobei
, wobei  die kleine Halbachse ist. Somit gilt
die kleine Halbachse ist. Somit gilt
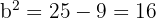
Die kleine Halbachse misst somit  .
.
Mittelpunktsgleichung:
Da wir bereits die Werte für  und
und  haben sowie den Mittelpunkt — der Punkt in der Mitte der Brennpunkte, also
haben sowie den Mittelpunkt — der Punkt in der Mitte der Brennpunkte, also  — ist die Mittelpunktsgleichung gegeben durch
— ist die Mittelpunktsgleichung gegeben durch

Exzentrizität:
Schließlich ist die Exzentrizität der Ellipse gegeben durch
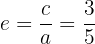
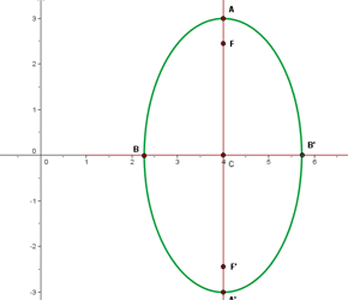
Gegeben ist die Mittelpunktsgleichung der Ellipse 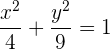 . Bestimme die Korrdinaten der Scheitelpunkte, der Nebenscheitelpunkte, der Brennpunkte und die Exzentrizität.
. Bestimme die Korrdinaten der Scheitelpunkte, der Nebenscheitelpunkte, der Brennpunkte und die Exzentrizität.
Anhand der Gleichung können wir sehen, dass der Mittelpunkt der Ellipse im Ursprung liegt. Außerdem gilt

Die Scheitelpunkte haben also folgende Koordinaten
 ,
,
da die Hauptachse auf der  -Achse liegt. Die Nebenscheitelpunkte liegen bei
-Achse liegt. Die Nebenscheitelpunkte liegen bei

Die halbe Brennweite ist
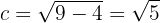
Die Brennpunkte befinden sich bei
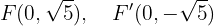
Schließlich wird die Exzentrizität wie folgt berechnet
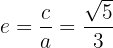
Gegeben ist die Ellipse mit der Gleichung 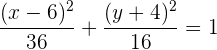 . Bestimme ihren Mittelpunkt, Halbachsen, Scheitelpunkte, Nebenscheitelpunkte und Brennpunkte.
. Bestimme ihren Mittelpunkt, Halbachsen, Scheitelpunkte, Nebenscheitelpunkte und Brennpunkte.
Anhand der Gleichung sehen wir sofort, dass der Mittelpunkt  ist. Die kleine und große Halbachse sind
ist. Die kleine und große Halbachse sind
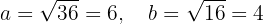
Somit
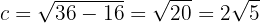
Die Scheitelpunkte befinden sich also bei 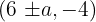 , es decir
, es decir
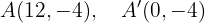
Die Brennpunkte befinden sich bei

Die Nebenscheitelpunkte sind
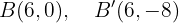
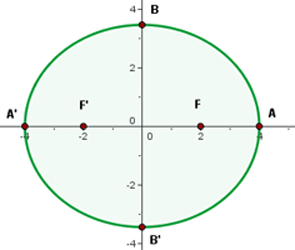
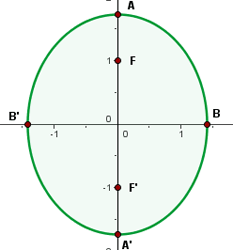
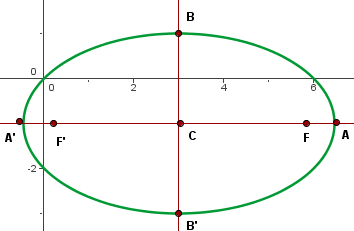
Stelle grafisch dar und bestimme die Koordinaten der Brennpunkte, Scheitelpunkte, Nebenscheitelpunkte und die Exzentrizität der folgenden Ellipsen.
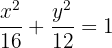
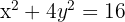

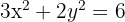
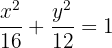
Der Mittelpunkt befindet sich im Ursprung. Die kleine und große Halbachse sind

Die Scheitelpunkte befinden sich bei
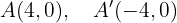
Die Nebenscheitelpunkte sind
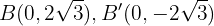
Die halbe Brennweite ist
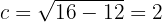
Daher befinden sich die Brennpunkte bei
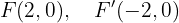
Schließlich ist die Exzentrizität

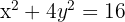
Zunächst müssen wir die Gleichung als Mittelpunktsgleichung schreiben und dividieren deshalb durch  :
:

Aus der Gleichung ergibt sich, dass der Mittelpunkt im Ursprung 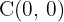 liegt und dass
liegt und dass

Daher befinden sich die Scheitelpunkte bei
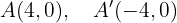
und die Nebenscheitelpunkte befinden sich bei

Außerdem ist die halbe Brennweite
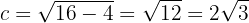
Somit befinden sich die Brennpunkte bei
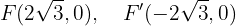
Schließlich ist die Exzentrizität gegeben durch


Die Gleichung steht bereits als Mittelpunktsgleichung. Aus dieser Gleichung geht hervor, dass der Mittelpunkt bei 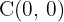 liegt. Außerdem sind die kleine und große Halbachse gegeben durch
liegt. Außerdem sind die kleine und große Halbachse gegeben durch
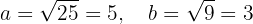
Die halbe Brennweite ist gegeben durch
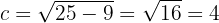
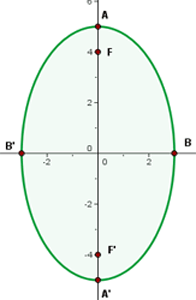
Wir stellen fest, dass die Hauptachse auf der  -Achse liegt. Die Scheitelpunkte befinden sich also bei
-Achse liegt. Die Scheitelpunkte befinden sich also bei
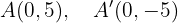
Die Nebenscheitelpunkte befinden sich bei

Und die Brennpunkte sind die Punkte
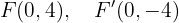
Schließlich ist die Exzentrizität gegeben durch

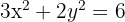
Schließlich haben wir eine Gleichung, die nicht in der Form der Mittelpunktsgleichung vorliegt. Wir dividieren zunächst durch  und erhalten
und erhalten
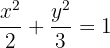
Aus der Gleichung geht hervor, dass

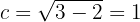
Wir sehen außerdem, dass die Hauptachse auf der  -Achse liegt. Die Scheitelpunkte befinden sich also bei
-Achse liegt. Die Scheitelpunkte befinden sich also bei
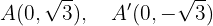
Die Nebenscheitelpunkte sind die Punkte

Die Brennpunkte sind die Punkte
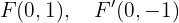
Schließlich ist die Exzentrizität
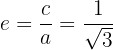
Stelle grafisch dar und bestimme die Koordinaten der Brennpunkte, Scheitelpunkte und Nebenscheitelpunkte der folgenden Ellipsen.

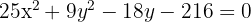



Um die wichtigen Punkte der Ellipse zu bestimmen, müssen wir ihre Gleichung als Mittelpunktsgleichung schreiben. Der Weg dazu ist die quadratische Ergänzung:
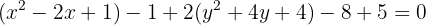
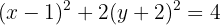
Schließlich dividieren wir durch  ,
,
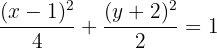
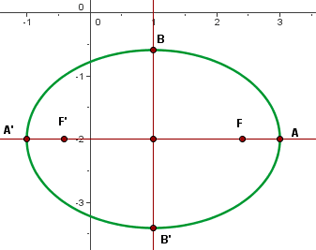
Es ist also klar, dass der Mittelpunkt bei  liegt. Außerdem kann man feststellen, dass
liegt. Außerdem kann man feststellen, dass
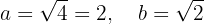
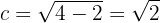
Zudem verläuft die Hauptachse horizontal, so dass sich die Scheitelpunkte bei
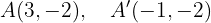 befinden
befinden
Die Nebenscheitelpunkte befinden sich bei

Und die Brennpunkte befinden sich bei

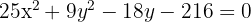
Wir wenden wieder die quadratische Ergänzung an:
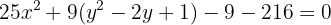

Schließlich dividieren wir durch  ,
,
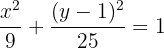
Es ist also klar, dass der Mittelpunkt bei  liegt. Außerdem kann man feststellen, dass
liegt. Außerdem kann man feststellen, dass
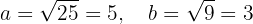
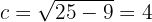
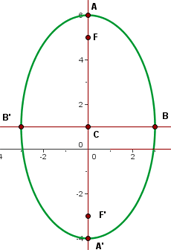
Außerdem verläuft die Hauptachse vertikal, so dass sich die Scheitelpunkte bei
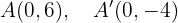 befinden
befinden
Die Nebenscheitelpunkte befinden sich bei
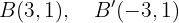
Und die Brennpunkte befinden sich bei


Wir wenden wieder die quadratische Ergänzung an:
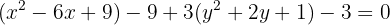
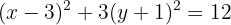
Schließlich dividieren wir durch  ,
,
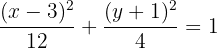
Es ist also klar, dass der Mittelpunkt bei  liegt. Außerdem kann man feststellen, dass
liegt. Außerdem kann man feststellen, dass
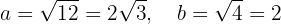

Außerdem verläuft die Hauptachse horizontal, so dass sich die Scheitelpunkte bei
 befinden
befinden
Die Nebenscheitelpunkte befinden sich bei
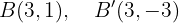
Und die Brennpunkte befinden sich bei


Wir wenden wieder die quadratische Ergänzung an:


Schließlich dividieren wir durch  ,
,
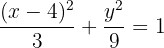
Es ist also klar, dass der Mittelpunkt bei  liegt. Außerdem kann man feststellen, dass
liegt. Außerdem kann man feststellen, dass
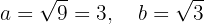
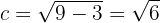
Außerdem verläuft die Hauptachse vertikal, so dass folgende Punkte sind

Die Nebenscheitelpunkte befinden sich bei

Und die Brennpunkte befinden sich bei
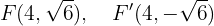
Bestimme die Koordinaten des Mittelpunkts der Sehne, die die Gerade 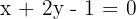 mit der Ellipse schneidet, deren Gleichung
mit der Ellipse schneidet, deren Gleichung 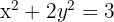 lautet.
lautet.
Sieh dir zunächst die Abbildung der Geraden und der Ellipse an:
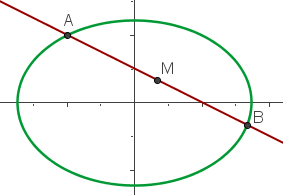
Aus der Abbildung können wir ableiten, dass wir die Koordinaten der Punkte  und
und  finden müssen. Dann ist
finden müssen. Dann ist  der Mittelpunkt dieser beiden Punkte.
der Mittelpunkt dieser beiden Punkte.
Die Bestimmung der Koordinaten von  und
und  ist gleichbedeutend mit der Lösung des folgenden nichtlinearen Gleichungssystems
ist gleichbedeutend mit der Lösung des folgenden nichtlinearen Gleichungssystems
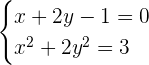
Auch dieses System wird durch Substitution gelöst. Die Lösungen sind gegeben durch

Der Mittelpunkt der Sehne ist also gegeben durch
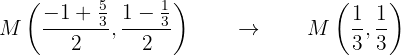
Mit KI zusammenfassen:












