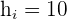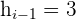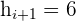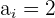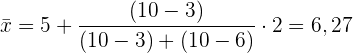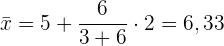Kapitel
Definition des Modus
- Der Modus ist der Wert mit der größten absoluten Häufigkeit.
- Die Notation ist
. - Wenn es in einer Gruppe zwei oder mehrere Werte mit der gleichen Häufigkeit gibt und diese Häufigkeit die maximale Häufigkeit ist, ist die Verteilung somit bimodal (falls es
Werte gibt) oder multimodal (falls es mehr als Werte gibt). Es gibt also meherere Modi. - Wenn alle Werte einer Gruppe die gleiche Häufigkeit haben, gibt es keinen Modus.
- Der Modus kann für qualitative und quantitative Variablen ermittelt werden.
- Wenn zwei nebeneinanderliegende Werte die größte Häufigkeit haben, ist der Modus der Durchschnitt dieser beiden Werte.
Beispiele für die Berechnung des Modus
1 Bestimme den Modus der Verteilung: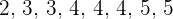 
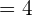
2 Bestimme den Modus der Verteilung: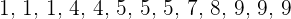
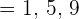
3 Bestimme den Modus der Verteilung: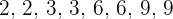 
Da die Werte der Gruppe die gleiche Häufigkeit haben, gibt es keinen Modus.
4 Bestimme den Modus der Verteilung: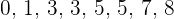 
Den Modus für gruppierte Daten berechnen
Fall 1: Die Intervalle sind gleich groß.
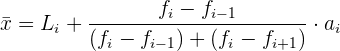
ist die Untergrenze der Modalklasse
ist die absolute Häufigkeit der Modalklasse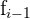
ist die absolute Häufigkeit direkt unterhalb der Modalklasse
ist die absolute Häufigkeit direkt oberhalb der Modalklasse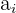
ist die Klassenbreite
Es wird auch eine andere Formel für den Modus angewendet; diese liefert einen ungefähren Wert:
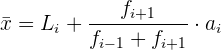
Beispiel:
Berechne den Modus einer statistischen Verteilung, die durch folgende Tabelle gegeben ist:
| |
|---|---|
 |  |
 |  |
 |  |
 |  |
 |  |
 |
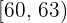Zunächst suchen wir das Intervall, indem der Modus liegt; dies ist das Intervall mit der größten absoluten Häufigkeit 
.
Die Modalklasse ist:
Wir wenden die Formel zur Berechnung des Modus für gruppierte Daten und erhalten:
Untergrenze: 
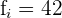
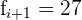
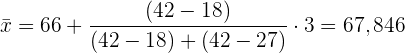
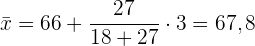
Fall 2: Die Breite der Intervalle ist unterschiedlich.
1 Als Erstes müssen wir die Höhen berechnen.
2 Die Modalklasse ist die Klasse mit der größten Häufigkeitsdichte.
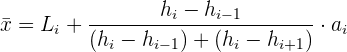
3 Die Formel zur Berechnung des ungefähren Modus bei unterschiedlichen Klassenbreiten lautet:
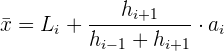
Beispiel:
Die folgende Tabelle zeigt die Noten (nicht bestanden, bestanden, bestanden, gut und hervorragend), die eine Gruppe von 50 Schülern erhalten hat. Berechne den Modus.
| |
|---|---|
 |  |
 |  |
 |  |
 |  |
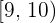Zunächst erstellen wir eine neue Spalte mit den Höhen, indem wir die absoluten Häufigkeiten durch die Breiten der entsprechenden Intervalle teilen:
|  | |
|---|---|---|
| | |
| |  |
| |  |
| | |
 |
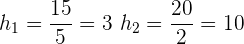
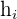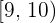Die Modalklasse ist
Untergrenze:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
