Kapitel

Additon, Multiplikation und Potenz von Matrizen
Gegeben sind die Matrizen:

Führe folgende Rechenoperationen durch:
1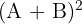
2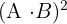
3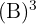
4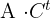
1 Um die Aufgabe zu lösen, folgen wir der Hierarchie der Rechenoperationen, d. h. wir addieren zunächst die Matrizen: 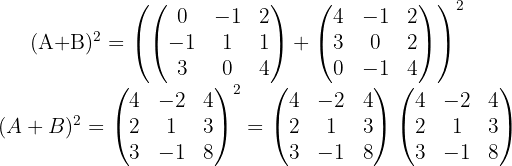 Anschließend berechnen wir das Quadrat der Matrix:
Anschließend berechnen wir das Quadrat der Matrix: 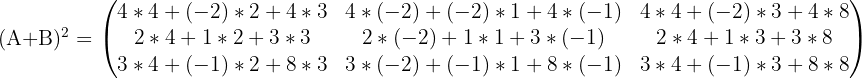 Schließlich erhalten wir durch die Berechnungen:
Schließlich erhalten wir durch die Berechnungen: 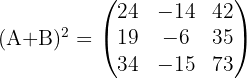
2 Um diese Aufgabe zu lösen, berechnen wir zunächst das Produkt der Matrizen: 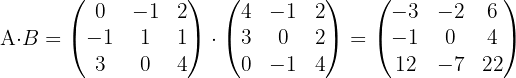 Anschließend berechnen wir das Quadrat der Matrix:
Anschließend berechnen wir das Quadrat der Matrix: 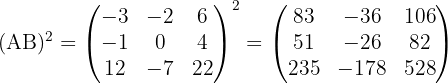
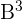 als
als 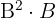 . Sowie
. Sowie 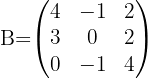
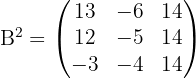
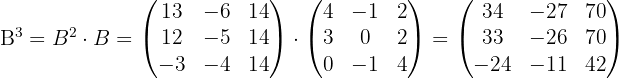
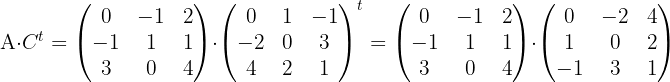
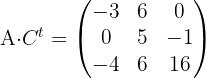
Dimension von Matrizen
Gegeben sind die Matrizen: 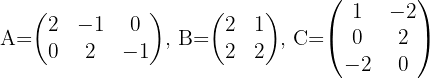 . Erkläre für jeden der folgenden Ausdrücke, in welchen Fällen es möglich ist, das Produkt zu berechnen, und in welchen Fällen nicht.
. Erkläre für jeden der folgenden Ausdrücke, in welchen Fällen es möglich ist, das Produkt zu berechnen, und in welchen Fällen nicht.
1 
2 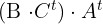
3 Ermittle die Dimension von  , damit das Produkt
, damit das Produkt 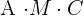 gebildet werden kann.
gebildet werden kann.
4 Bestimme die Dimension von  , sodass
, sodass  eine quadratische Matrix ist.
eine quadratische Matrix ist.
Bevor die Lösungen betrachtet werden, ist es wichtig zu wissen, dass die Notation für die Dimension einer Matrix  , die aus
, die aus  Zeilen und
Zeilen und  Spalten besteht, wie folgt bezeichnet wird:
Spalten besteht, wie folgt bezeichnet wird:  . Um die Multiplikation zweier Matrizen durchzuführen, muss außerdem sichergestellt sein, dass: Die Anzahl der Spalten der ersten Matrix muss gleich der Anzahl der Zeilen der zweiten Matrix sein (mit der Besonderheit, dass die aus dem Produkt erhaltene Matrix die gleiche Anzahl von Zeilen wie die erste Matrix und die gleiche Anzahl von Spalten wie die zweite Matrix hat).
. Um die Multiplikation zweier Matrizen durchzuführen, muss außerdem sichergestellt sein, dass: Die Anzahl der Spalten der ersten Matrix muss gleich der Anzahl der Zeilen der zweiten Matrix sein (mit der Besonderheit, dass die aus dem Produkt erhaltene Matrix die gleiche Anzahl von Zeilen wie die erste Matrix und die gleiche Anzahl von Spalten wie die zweite Matrix hat).
1 Um festzustellen, ob es möglich ist, das Produkt  zu berechnen, müssen wir die Dimensionen der beteiligten Matrizen analysieren:
zu berechnen, müssen wir die Dimensionen der beteiligten Matrizen analysieren:  ist eine Matrix der Dimension
ist eine Matrix der Dimension  , weshalb
, weshalb 
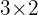 ist.
ist.  ist eine Matrix der Dimension
ist eine Matrix der Dimension  .
.  ist eine Matrix der Dimension
ist eine Matrix der Dimension 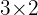 . Dies kann folgendermaßen ausgedrückt werden:
. Dies kann folgendermaßen ausgedrückt werden: 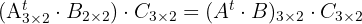
Da die Anzahl der Spalten von 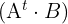 nicht mit der Anzahl der Zeilen von
nicht mit der Anzahl der Zeilen von  übereinstimmt, kann die Rechenoperation nicht durchgeführt werden.
übereinstimmt, kann die Rechenoperation nicht durchgeführt werden.
2  Wir stellen fest:
Wir stellen fest:  ist eine Matrix der Dimension
ist eine Matrix der Dimension 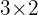 .
.  ist eine Matrix der Dimension
ist eine Matrix der Dimension  .
.  ist eine Matrix der Dimension
ist eine Matrix der Dimension 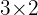 , weshalb
, weshalb 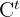 eine Matrix der Dimension
eine Matrix der Dimension  ist. Wir schreiben um:
ist. Wir schreiben um: 
Daher kann die Rechenoperation durchgeführt werden; insbesondere hat die resultierende Matrix die Dimension  .
.
3 Bestimme die Dimension von  , so dass das Produkt
, so dass das Produkt 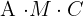 hergestellt werden kann.
hergestellt werden kann.
Beachte, dass die Multiplikation zweier Matrizen voraussetzt, dass die Anzahl der Spalten der ersten Matrix gleich der Anzahl der Zeilen der zweiten ist.  ist eine Matrix der Dimension
ist eine Matrix der Dimension  . d. h. zwei Zeilen und drei Spalten. Also muss
. d. h. zwei Zeilen und drei Spalten. Also muss  drei Zeilen haben. Das heißt:
drei Zeilen haben. Das heißt: 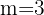
4 Bestimme die Dimension von  , so dass
, so dass 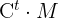 eine quadratische Matrix ist. Die Matrix
eine quadratische Matrix ist. Die Matrix  hat die Dimension
hat die Dimension 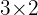 , weshalb ihre transponierte Matrix die Dimension
, weshalb ihre transponierte Matrix die Dimension  hat. Um sie mit
hat. Um sie mit  zu multiplizieren, muss die Anzahl der Spalten von
zu multiplizieren, muss die Anzahl der Spalten von 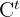 der Anzahl der Zeilen von
der Anzahl der Zeilen von  entsprechen, also
entsprechen, also 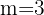 .
.
Das Produkt von 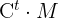 ist eine Matrix mit der gleichen Anzahl von Zeilen wie
ist eine Matrix mit der gleichen Anzahl von Zeilen wie 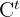 , also
, also  , und der gleichen Anzahl von Spalten wie
, und der gleichen Anzahl von Spalten wie  . Da das Produkt eine quadratische Matrix ist, muss die Anzahl der Spalten von
. Da das Produkt eine quadratische Matrix ist, muss die Anzahl der Spalten von  ebenfalls 2 sein. Somit hat die Matrix
ebenfalls 2 sein. Somit hat die Matrix  die Dimension
die Dimension 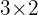 .
.
Kommutativität von Matrizen
Berechne alle Matrizen, die mit folgender Matrix kommutativ sind: 
Wir müssen beachten, dass für die Kommutativität zweier Matrizen gelten muss, dass  . Wenn wir
. Wenn wir 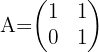 und
und 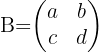 nehmen, haben wir folgende Gleichheit:
nehmen, haben wir folgende Gleichheit:
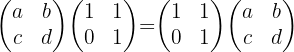
Wir führen die Berechnungen auf beiden Seiten durch und erhalten:
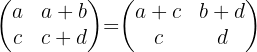
Daraus lassen sich die folgenden Gleichheiten ableiten:

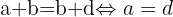


Die Matrix muss somit wie folgt aussehen: 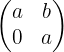
Matrizengleichungen
Gegeben ist 
Löse die Matrizengleichung
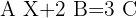
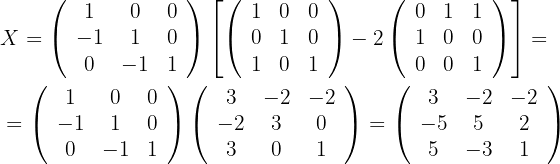
Um den Wert von  zu berechnen, müssen wir auf beiden Seiten der Gleichheit Rechenoperationen durchführen. Zuerst subtrahieren wir auf beiden Seiten
zu berechnen, müssen wir auf beiden Seiten der Gleichheit Rechenoperationen durchführen. Zuerst subtrahieren wir auf beiden Seiten  und multiplizieren dann mit der inversen Matrix von
und multiplizieren dann mit der inversen Matrix von  wie nachstehend gezeigt:
wie nachstehend gezeigt: 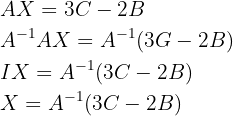 Sobald wir die Lösung ausgedrückt haben, berechnen wir die inverse Matrix von
Sobald wir die Lösung ausgedrückt haben, berechnen wir die inverse Matrix von  :
: 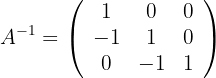 . Schließlich setzen wir ein und berechnen:
. Schließlich setzen wir ein und berechnen:
Praktische Anwendung von Matrizen
Eine Möbelfirma stellt drei Modelle von Regalen her: A, B und C. In jeder der Größen, groß und klein. Täglich werden 1000 große und 8000 kleine Regale vom Typ A, 8000 große und 6000 kleine Regale vom Typ B und 4000 große und 6000 kleine Regale vom Typ C hergestellt. Jedes große Regal hat 16 Schrauben und 6 Halterungen, und jedes kleine Regal hat 12 Schrauben und 4 Halterungen. Dies gilt für alle drei Modelle.
1 Stelle diese Information in zwei Matrizen dar.
2 Finde eine Matrix, die die Anzahl der Schrauben und Halterungen darstellt, die für die tägliche Produktion jedes der sechs Regalmodelle erforderlich sind.
Eine Möbelfirma stellt drei Modelle von Regalen her: A, B und C. In jeder der Größen, groß und klein. Täglich werden 1000 große und 8000 kleine Regale vom Typ A, 8000 große und 6000 kleine Regale vom Typ B und 4000 große und 6000 kleine Regale vom Typ C hergestellt. Jedes große Regal hat 16 Schrauben und 6 Halterungen, und jedes kleine Regal hat 12 Schrauben und 4 Halterungen. Dies gilt für alle drei Modelle.
Zeilen: Modelle A, B, C Spalten: Typen G, P
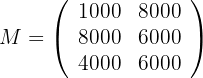
Matrix der Elemente der Regale:
Zeilen: Typen G, P Spalten: T, S
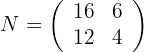
Matrix, die die Anzahl der Schrauben und Halterungen für jedes Regalmodell angibt:
Zeilen: Modelle A, B, C Spalten: Typen T, S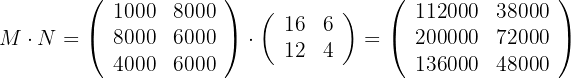
Mit KI zusammenfassen:












