Grundlegende Rechenoperationen mit Matrizen
Gegeben sind die Matrizen:
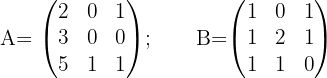
Berechne:
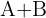
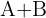
Wir addieren die Elemente, deren Position in beiden Matrizen übereinstimmt:
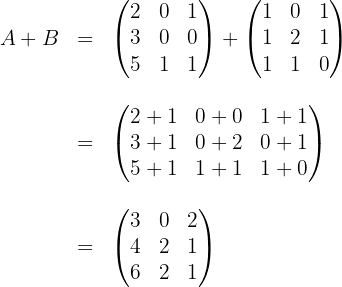
Grundlegende Rechenoperationen mit Matrizen
Gegeben sind die Matrizen:
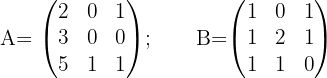
Berechne:
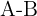
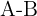
Wir subtrahieren die Elemente, deren Position in beiden Matrizen übereinstimmt:

Grundlegende Rechenoperationen mit Matrizen
Gegeben sind die Matrizen:
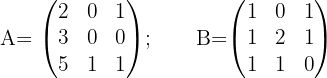
Berechne:


Wir multiplizieren die Zeile  mit der Spalte
mit der Spalte  , um das Element
, um das Element  zu erhalten
zu erhalten

Grundlegende Rechenoperationen mit Matrizen
Gegeben sind die Matrizen:
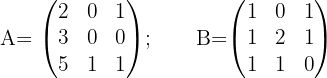
Berechne:


Wir multiplizieren die Zeile  mit der Spalte
mit der Spalte  , um das Element
, um das Element 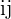 zu erhalten
zu erhalten

Grundlegende Rechenoperationen mit Matrizen
Gegeben sind die Matrizen:
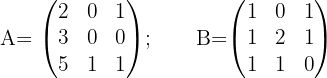
Berechne:
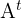
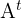
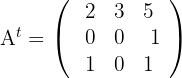
Zeige, dass folgende Annahme stimmt
Zeige, dass gilt: 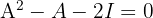 , wobei:
, wobei:
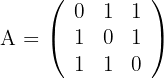
1 Wir berechnen 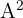

2 Wir ersetzen auf der linken Seite der Gleichung und berechnen

Somit haben wir bewiesen, dass die Annahme richtig ist.
n-te Potenz einer Matrix
Angenommen,  ist die Matrix
ist die Matrix 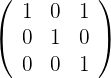 .
.
Bestimme 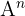 für
für 
1 Wir berechnen 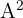

2 Wir berechnen 
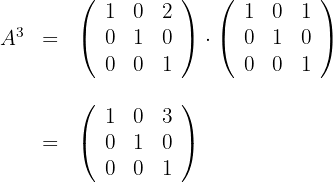
3 Wir stellen fest, dass das Element auf der Position  mit der Potenz von
mit der Potenz von  übereinstimmt, weshalb wir die Potenz als
übereinstimmt, weshalb wir die Potenz als  angeben
angeben

4 Wir sehen uns an, ob die vorgeschlagene Formel für die Potenz  gilt
gilt
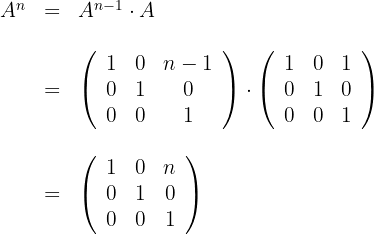
Wir wissen nun, dass die vorgeschlagene Formel für irgendeine Potenz  gilt
gilt
Inverse Matrix
Berechne die inverse Matrix für:

1 Erstelle eine Matrix vom Typ 

2 Wende den Gauß-Jordan-Algorithmus an, um die linke Hälfte,  , in die Einheitsmatrix umzuwandeln. Die Matrix, die auf der rechten Seite resultiert, ist die inverse Matrix
, in die Einheitsmatrix umzuwandeln. Die Matrix, die auf der rechten Seite resultiert, ist die inverse Matrix  .
.
Wir berechnen 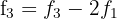

Wir berechnen  y
y 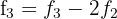
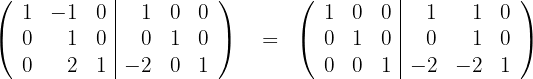
3 Die inverse Matrix ist
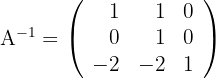
Gleichungssysteme mit Matrizen
Ermittle die Matrizen  und
und  , die das folgende Gleichungssystem bestätigen:
, die das folgende Gleichungssystem bestätigen:
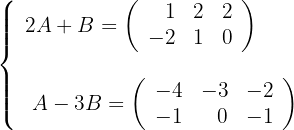
1 Wir multiplizieren die zweite Gleichung mit 

2 Wir addieren die einzelnen Elemente und lösen nach  auf
auf

3 Wenn wir die erste Gleichung mit 3 multiplizieren und Element für Element addieren, erhalten wir:
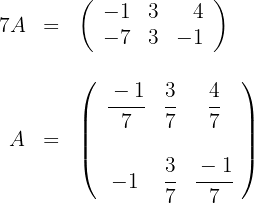
Problemanalyse mit Hilfe von Matrizen
Eine Fabrik produziert zwei Modelle von Waschmaschinen,  und
und  , in drei Ausführungen:
, in drei Ausführungen:  und
und  .
.
Es werden vom Modell  Einheiten in der Ausführung
Einheiten in der Ausführung  ,
,  Einheiten in der Ausführung
Einheiten in der Ausführung  und
und  Einheiten in der Ausführung
Einheiten in der Ausführung  produziert.
produziert.
Es werden vom Modell 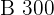 Einheiten in der Ausführung
Einheiten in der Ausführung  ,
,  Einheiten in der Ausführung
Einheiten in der Ausführung  und
und  Einheiten in der Ausführung
Einheiten in der Ausführung  produziert.
produziert.
Für Ausführung  sind
sind  Produktionsstunden und
Produktionsstunden und  Verwaltungsstunden nötig. Für Ausführung
Verwaltungsstunden nötig. Für Ausführung  sind
sind  Produktionsstunden und
Produktionsstunden und  Verwaltungsstunden nötig. Für Ausführung
Verwaltungsstunden nötig. Für Ausführung  sind
sind  Produktionsstunden und
Produktionsstunden und 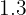 Verwaltungsstunden nötig.
Verwaltungsstunden nötig.
1 Stelle die Gegebenheiten in Form von zwei Matrizen dar.
2 Bestimme für jedes einzelne der Modelle eine Matrix, die die Stunden für Produktion und Verwaltung darstellt.
Matrix für die Produktion:
Zeilen: Modelle  ; Spalten: Ausführungen
; Spalten: Ausführungen 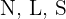
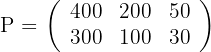
Matrix für den Aufwand in Stunden:
Zeilen: Ausführungen 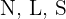 ; Spalten: Aufwand in Stunden:
; Spalten: Aufwand in Stunden: 
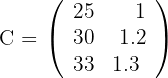
Matrix, die die Stunden der Produktion und Verwaltung für jedes einzelne Modell ausdrückt:

Rang einer Matrix
Berechne den Rang der folgenden Matrix:

span class="sa">1 Wir rechnen 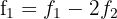
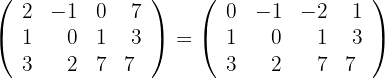
span class="sa">2 Wir rechnen 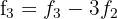
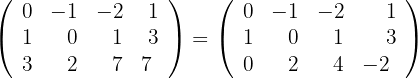
span class="sa">3 Wir rechnen 

Deshalb gilt 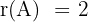 .
.
Gleichungen mit Unbekannten in Matrizen
Gegeben ist:
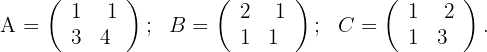
Berechne den Wert von  in den folgenden Gleichungen:
in den folgenden Gleichungen:
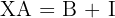
Wir bestimmen die Variable  in jeder der Gleichungen
in jeder der Gleichungen
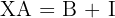
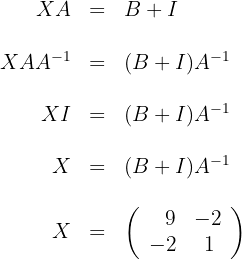
Gleichungen mit Unbekannten in Matrizen
Gegeben ist:
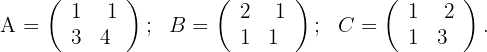
Berechne den Wert von  in den folgenden Gleichungen:
in den folgenden Gleichungen:
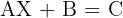
Wir bestimmen die Variable  in jeder der Gleichungen
in jeder der Gleichungen
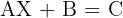

Gleichungen mit Unbekannten in Matrizen
Gegeben ist:
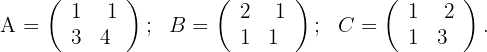
Berechne den Wert von  in den folgenden Gleichungen:
in den folgenden Gleichungen:
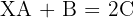
Wir bestimmen die Variable  in jeder der Gleichungen
in jeder der Gleichungen
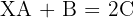
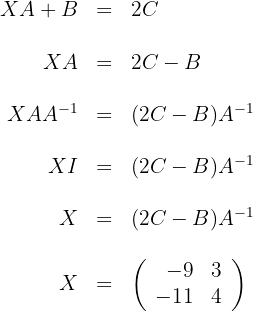
Gleichungen mit Unbekannten in Matrizen
Gegeben ist:
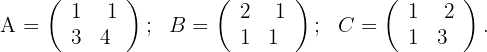
Berechne den Wert von  in den folgenden Gleichungen:
in den folgenden Gleichungen:
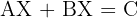
Wir bestimmen die Variable  in jeder der Gleichungen
in jeder der Gleichungen

Gleichungen mit Unbekannten in Matrizen
Gegeben ist:
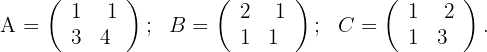
Berechne den Wert von  in den folgenden Gleichungen:
in den folgenden Gleichungen:

Wir bestimmen die Variable  in jeder der Gleichungen
in jeder der Gleichungen
Wir bestimmen die Variable  in jeder der Gleichungen
in jeder der Gleichungen
Von einem Gleichungssystem zu einer Matrix
Löse das System in Form einer Matrix:
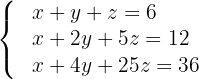
1 Wir schreiben in Form einer Matrix
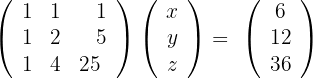
2 Wir lösen die Gleichung
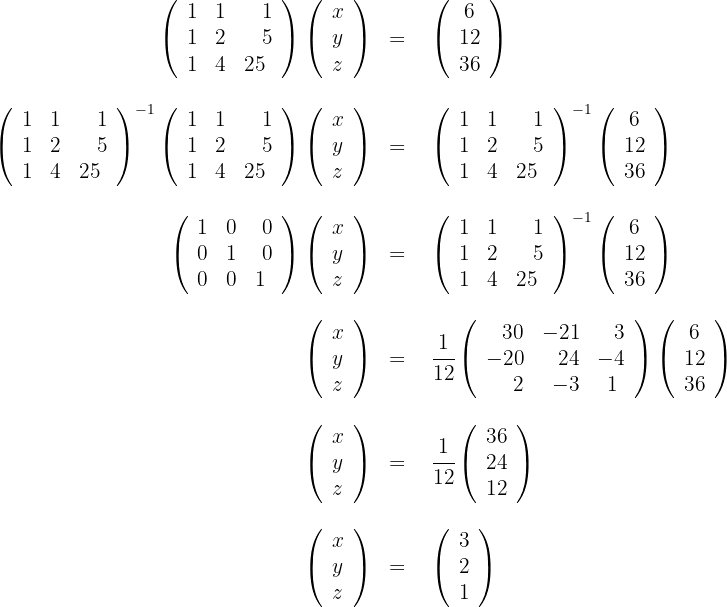
3 Somit ist die Lösung
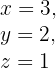
Mit KI zusammenfassen:



