Kapitel
Grundlegende Rechenoperationen mit Matrizen
Addition von Matrizen
Gegeben sind zwei Matrizen mit der gleichen Dimension,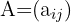 
und 
. Die Summe der Matrizen wird wie folgt definiert: 
. Das heißt, jene Matrix, deren Elemente durch Addition der Elemente der beiden Matrizen, die dieselbe Position einnehmen, erhalten werden:
Das Gleiche gilt für die übrigen Matrizen,
Beispiel:
Produkt aus einer reellen Zahl und einer Matrix
Bei einer Matrix 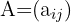und einer reellen Zahl 
wird das Produkt aus einer reellen Zahl und einer Matrix wie folgt definiert: die Matrix derselben Ordnung wie 
, wobei jedes Element mit multipliziert wird.
Beispiel:
Produkt aus Matrizen
Zwei Matrizen und 
können multipliziert werden, wenn die Anzahl der Spalten von mit der Anzahl der Zeilen von übereinstimmt.
Das Element 
der Produktmatrix erhält man, indem man jedes Element der Zeile 
der Matrix mit jedem Element der Spalte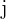 
der Matrix multipliziert und schließlich addiert.
Beispiel:
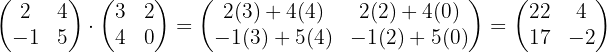
Eigenschaften der inversen Matrix
Wir definieren die inverse Matrix 
als Produkt der Ausgangsmatrix und entspricht der Einheitsmatrix. Das heißt,
Außerdem gelten folgende Eigenschaften:
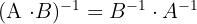
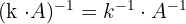
Berechnung mit dem Gauß-Verfahren
Gegeben ist , eine quadratische Matrix der Ordnung 
. Um die inverse Matrix von zu berechnen, die wir als bezeichnen, gehen wir wie folgt vor:
1 Bilde eine Matrix vom Typ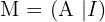 
. Das heißt, befindet sich auf der linken Hälfte von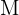 
und die Einheitsmatrix 
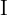auf der rechten.
2 Unter Verwendung des Gauß-Verfahrens transformieren wir die linke Hälfte, , in die Einheitsmatrix, die sich nun auf der rechten Seite befindet, und die resultierende Matrix auf der rechten Seite ist dann die inverse Matrix: .
Berechnung durch Determinanten
Wobei die inverse Matrix ist,
die Determinante der Matrix ist,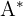
die Adjunkte ist,
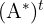die transponierte Matrix der Adjunkten ist.
Rang einer Matrix
Rang einer Matrix: Dies ist die Anzahl der Zeilen dieser Matrix (Zeilen oder Spalten), die linear unabhängig sind.
Wir können eine Linie ziehen, wenn:
Alle ihre Koeffizienten 0 sind.
Es zwei gleiche Linien gibt.
Eine Linie proportional zur anderen ist.
Eine Linie eine Linearkombination anderer ist.
Berechnung mit dem Gauß-Verfahren
Im Allgemeinen werden so viele Zeilen wie möglich auf 0 gesetzt, und der Rang entspricht der Anzahl der Zeilen, die nicht 0 sind.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
