Kapitel

Gleichungen mit Matrizen
Gegeben sind folgende Matrizen:

Löse folgende Gleichung:

1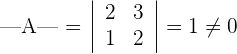
Dies besagt uns, dass die Matrix  invertierbar ist.
invertierbar ist.
2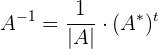
wobei gilt

Die adjungierte Matrix ist in diesem Fall:
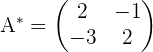
Die transponierte Matrix der adjungierten ist: 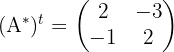
Deshalb ist die inverse Matrix der Matrix  :
: 
3


 ist hierbei die Einheitsmatrix (in diesem Fall
ist hierbei die Einheitsmatrix (in diesem Fall  ).
).
4
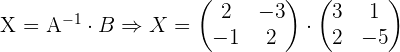

Gegeben sind die Matrizen:

Löse folgende Gleichung:

1
21 & 1\\
1 & 2
\end{vmatrix}=1\neq 0[/latex]
Wir stellen fest, dass  invertierbar ist. Für die inverse Matrix von
invertierbar ist. Für die inverse Matrix von  gilt:
gilt: 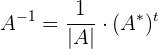
Wobei gilt  Durch unsere Berechnungen erhalten wir:
Durch unsere Berechnungen erhalten wir: 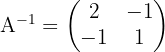
3Wir ersetzen die Werte für  ,
,  und
und  und erhalten:
und erhalten: 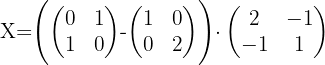
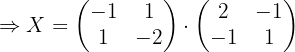

Löse die folgenden Gleichungen (3 Matrizen kennst du schon)
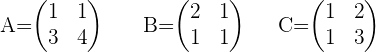
Berechne den Wert von  in den folgenden Gleichungen:
in den folgenden Gleichungen:

1 Nutze die Rechenregeln für Matrizen, um die Gleichung umzuformen.
Zuerst müssen wir  in der Gleichung bestimmen:
in der Gleichung bestimmen:
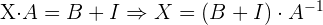
 bedeutet hier die Einheitsmatrix (in diesem Fall
bedeutet hier die Einheitsmatrix (in diesem Fall  ).
).
2 Wir berechnen die inverse Matrix von  .
.
Zunächst überprüfen wir, ob  invertierbar ist. Dazu müssen wir die Determinante berechnen:
invertierbar ist. Dazu müssen wir die Determinante berechnen:
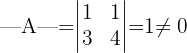
Dies sagt uns, dass die Matrix  invertierbar ist.
invertierbar ist.
Die inverse Matrix von  ist gegeben durch:
ist gegeben durch:
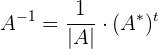
wobei gilt

Durch die Berechnungen erhalten wir:
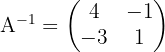
3 Wir ersetzen die gefundenen Werte und lösen die Gleichung:
Wir haben die Gleichung:
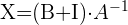
Wir ersetzen die Werte für  ,
,  und
und  , und erhalten:
, und erhalten:
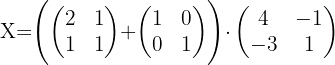
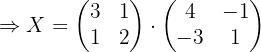
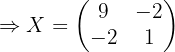

1 Die Gleichung mithilfe der Regeln für das Rechnen mit Matrizen umschreiben.
Zunächst müssen wir  in der Gleichung bestimmen:
in der Gleichung bestimmen:

2 Wir berechnen die inverse Matrix von  .
.
Aus Aufgabe  wissen wir, die inverse Matrix von
wissen wir, die inverse Matrix von  ist:
ist:
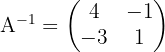
3 Wir ersetzen die gefundenen Werte und lösen die Gleichung:
Wir haben die Gleichung:

Wir ersetzen die Werte für  ,
,  und
und  , und erhalten:
, und erhalten:

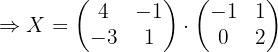
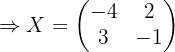

1 Die Gleichung mithilfe der Regeln für das Rechnen mit Matrizen umschreiben.
Zunächst müssen wir  in der Gleichung bestimmen:
in der Gleichung bestimmen:

2 Wir berechnen die inverse Matrix von  .
.
Aus Aufgabe  wissen wir, die inverse Matrix von
wissen wir, die inverse Matrix von  ist:
ist:
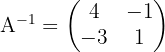
3 Wir ersetzen die gefundenen Werte und lösen die Gleichung:
Wir haben die Gleichung:

Wir ersetzen die Werte für  ,
,  und
und  , und erhalten:
, und erhalten:
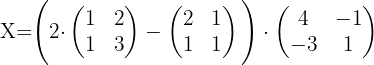
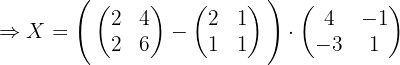
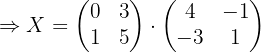
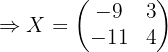
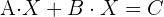
1 Die Gleichung mithilfe der Regeln für das Rechnen mit Matrizen umschreiben.
Zunächst müssen wir  in der Gleichung bestimmen:
in der Gleichung bestimmen:

2 Wir berechnen die inverse Matrix von 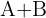 .
.
Zuerst müssen wir die Matrizen  und
und  addieren:
addieren:
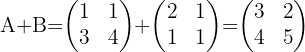
Für die inverse Matrix einer Matrix  gilt die folgende Formel:
gilt die folgende Formel:

wobei gilt

Durch unsere Berechnungen erhalten wir die inverse Matrix von 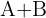 :
:
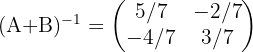
3 Wir ersetzen die gefundenen Werte und lösen die Gleichung:
Wir haben die Gleichung:

Wir ersetzen die Werte für 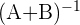 und
und  , und erhalten:
, und erhalten:
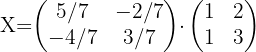
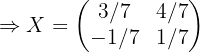

1 Die Gleichung mithilfe der Regeln für das Rechnen mit Matrizen umschreiben.
Zunächst müssen wir  in der Gleichung bestimmen:
in der Gleichung bestimmen:

2 Finde die Matrix, die sich aus  ergibt
ergibt
Wenn wir die Werte für  ,
,  und
und  ersetzen und die entsprechenden Rechenschritte durchführen, erhalten wir:
ersetzen und die entsprechenden Rechenschritte durchführen, erhalten wir:
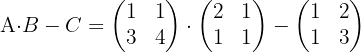
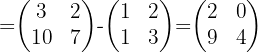
3 Bestimme die inverse Matrix von  .
.
Bevor wir die inverse Matrix bestimmen können, müssen wir überprüfen, ob die Matrix invertierbar ist. Dazu berechnen wir ihre Determinante.

 besagt uns, dass sie invertierbar ist. Nun ist die inverse Matrix einer Matrix
besagt uns, dass sie invertierbar ist. Nun ist die inverse Matrix einer Matrix  durch folgende Formel gegeben:
durch folgende Formel gegeben:

wobei gilt

Wenn wir also in diesem Fall die Berechnungen durchführen, sollten wir Folgendes erhalten:

4 Wir ersetzen die gefunden Werten und lösen die Gleichung:
Wir haben die Gleichung:
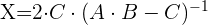
Wir ersetzen die Werte für 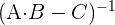 und
und  , und erhalten:
, und erhalten:
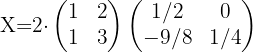
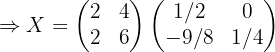
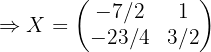
Matrizengleichungen
Gegeben sind folgende Matrizen:
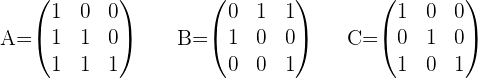
Löse die Gleichung:

1 Die Gleichung mithilfe der Regeln für das Rechnen mit Matrizen umschreiben.
Zuerst müssen wir  in der Gleichung bestimmen:
in der Gleichung bestimmen:
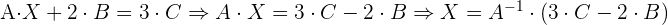
2 Bestimme die inverse Matrix von  .
.
Zuerst überprüfen wir, ob  invertierbar ist. Dazu müssen wir die Determinante wie folgt bestimmen:
invertierbar ist. Dazu müssen wir die Determinante wie folgt bestimmen:
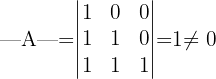
Dies besagt uns, dass die Matrix  invertierbar ist.
invertierbar ist.
Die inverse Matrix von  ist gegeben durch:
ist gegeben durch:
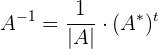
wobei gilt:

Durch unsere Berechnungen erhalten wir:

3 Wir ersetzen die gefunden Werte und lösen die Gleichung.
Wenn wir die Werte für  ,
,  und
und  in der Gleichung ersetzen und die Gleichung lösen, erhalten wir:
in der Gleichung ersetzen und die Gleichung lösen, erhalten wir:
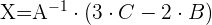

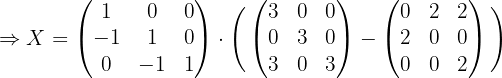

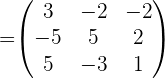
Gleichungssysteme mit Matrizen
Löse das Gleichungssystem in Form einer Matrix:
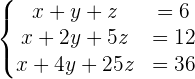
1 Schreibe das Gleichungssystem in eine Matrix um. Mit den Koeffizienten der Gleichungen können wir folgende Matrix erstellen:
Nun nehmen wir die drei Unbekannten 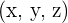 und bilden den Spaltenvektor:
und bilden den Spaltenvektor:
Schließlich nutzen wir die Lösungen der Gleichungen und schreiben sie wie folgt als Spaltenvektor:
Wenn wir die Gleichungen also in Form einer Matrix schreiben, erhalten wir: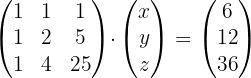


2 Bestimme die Inverse von  . Zunächst überprüfen wir, ob
. Zunächst überprüfen wir, ob  invertierbar ist. Dazu müssen wir die Determinante berechnen:
invertierbar ist. Dazu müssen wir die Determinante berechnen: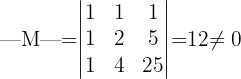
Dies besagt uns, dass die Matrix  invertierbar ist. Die inverse Matrix von
invertierbar ist. Die inverse Matrix von  ist gegeben durch:
ist gegeben durch: 
wobei gilt  Durch unsere Berechnungen erhalten wir:
Durch unsere Berechnungen erhalten wir: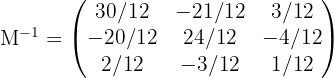
3 Wir ersetzen die gefundenen Werte und lösen die Gleichung. Wir haben folgende Gleichung:
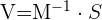
Wenn wir die Werte für 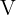 ,
, 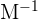 und
und  ersetzen und die Gleichung lösen, erhalten wir:
ersetzen und die Gleichung lösen, erhalten wir:
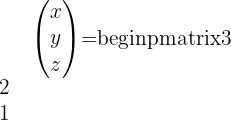
Dies bedeutet: 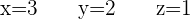
Berechnung von Matrizen in Gleichungssystemen
Bestimme die Matrizen A und B, um das Gleichungssystem zu überprüfen:

Wir multiplizieren die zweite Gleichung mit 
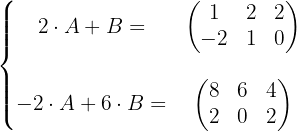
Wir addieren die erste und die zweite Gleichung und erhalten: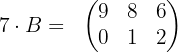
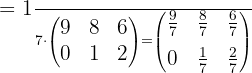
Nun nehmen wir die erste Gleichung und lösen nach  auf. Wir ersetzen dabei den für
auf. Wir ersetzen dabei den für  gefundenen Wert.
gefundenen Wert.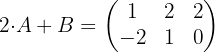
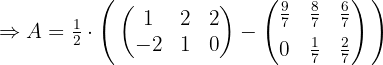

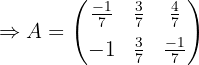
Löse die Gleichung:

Die Determinanten berechnen wir nicht.
Um diese Gleichung zu lösen, ohne die Determinanten zu berechnen, denken wir daran, dass die Determinante 0 ist, wenn der Rang der Matrix nicht vollständig ist. Dies ist gleichbedeutend damit, dass eine der Zeilen eine Linearkombination der beiden anderen ist. Wir benennen wie folgt:  für die erste Zeile,
für die erste Zeile,  für die zweite Zeile und
für die zweite Zeile und  für die dritte Zeile. Folglich ist die Determinante 0, wenn gilt:
für die dritte Zeile. Folglich ist die Determinante 0, wenn gilt: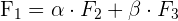
Wir können nun das folgende Gleichungssystem erstellen: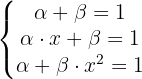
Wir denken daran, dass, obwohl es sich nicht um ein lineares System handelt, es 3 Variablen und 3 Gleichungen sind. Somit können wir sie lösen. Wir beginnen mit der Gleichsetzung der ersten beiden Gleichungen:
Hier gibt es zwei Fälle: 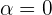 oder
oder  . Wenn
. Wenn  , können wir die Gleichung durch
, können wir die Gleichung durch  teilen, um
teilen, um  zu erhalten. Nehmen wir nun an, da
zu erhalten. Nehmen wir nun an, da 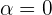 ist, dass aus der ersten Gleichung folgt:
ist, dass aus der ersten Gleichung folgt:
Deshalb ist 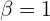 . Bei der dritten Gleichung haben wir dann:
. Bei der dritten Gleichung haben wir dann: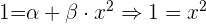
Daraus ergibt sich  . Die Lösungen sind also
. Die Lösungen sind also  und
und  .
.
Löse die Gleichung:
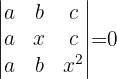
Die Determinanten berechnen wir nicht.
Die Determinante in dieser Aufgabe ist komplizierte als im vorherigen Beispiel. Dies liegt daran, dass wir arbiträre Einträge haben:  ,
,  und
und  .
.
Wenn wir jedoch alle Lösungen finden möchten, müssen wir wie in der vorhergehenden Aufgabe vorgehen. Wir benennen zunächst die Zeilen:  ,
,  und
und  . Somit ergibt sich folgendes Gleichunssystem:
. Somit ergibt sich folgendes Gleichunssystem: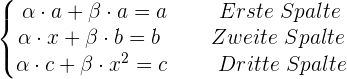
Wir stellen fest, dass die Variablen des Gleichungssystems  ,
,  und
und  sind. Die Buchstaben
sind. Die Buchstaben  ,
,  und
und  sind keine Variablen. Deshalb sind die Lösungen in den Termen
sind keine Variablen. Deshalb sind die Lösungen in den Termen  ,
,  und
und  zu finden. Wir haben wieder kein lineares Gleichungssystem. Wir beginnen mit der Bestimmung von
zu finden. Wir haben wieder kein lineares Gleichungssystem. Wir beginnen mit der Bestimmung von  in der ersten Gleichung und erhalten:
in der ersten Gleichung und erhalten: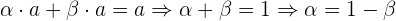
In diesem Fall nehmen wir an, dass 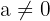 (im Fall von
(im Fall von 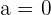 löst ein beliebiger Wert für
löst ein beliebiger Wert für  die Gleichung). Wenn wir den Wert für
die Gleichung). Wenn wir den Wert für  in der zweiten Gleichung ersetzen und
in der zweiten Gleichung ersetzen und  bestimmen, erhalten wir:
bestimmen, erhalten wir: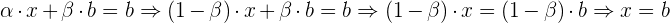
Somit ist  eine Lösung. Anstatt den Wert für
eine Lösung. Anstatt den Wert für 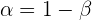 in der zweiten Gleichung zu ersetzen, ersetzen wir ihn in der dritten Gleichung:
in der zweiten Gleichung zu ersetzen, ersetzen wir ihn in der dritten Gleichung:
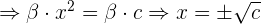
Somit sind unsere Lösungen:  und
und  .
.
Mit KI zusammenfassen:













