Willkommen auf unserer Seite mit Übungen und Aufgaben zum Modus in der Statistik! Superprof stellt dir diese Seite zur Verfügung, damit du mit Aufgaben üben und das Konzept des Modus in der Statistik besser verstehen kannst.
Der Modus ist ein deskriptives Maß, das den/die häufigsten Wert(e) in einem Datensatz identifiziert. Er stellt den Punkt oder die Punkte mit der größten Konzentration in der Verteilung der Daten dar.
Der Modus ist ein relativ einfach zu berechnendes Maß und kann für die Zusammenfassung von Daten über die am häufigsten vorkommenden Werte in einem Datensatz nützlich sein. Wie bei jedem deskriptiven Maß ist es jedoch wichtig, es in Verbindung mit anderen statistischen Maßen zu betrachten, um ein vollständiges Verständnis der Verteilung der Daten zu erhalten.
Unsere Website soll dir helfen, deine Fähigkeiten im Bereich des statistischen Modus zu vertiefen. Jede dieser Übungen wird dein Verständnis herausfordern und deine Problemlösungsfähigkeiten verbessern - je mehr du übst, desto mehr wirst du besser! Los geht's!
Berechne den Modus der folgenden Zahlenreihe:
.
table id=311 /]Die am häufigsten wiederholte Zahl ist 
. Der Modus 
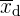ist also
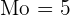
Ein Kinderarzt erhielt die folgende Tabelle auf der Grundlage des Alters von 
Kindern in seiner Praxis, die zum Zeitpunkt des ersten Gehens folgendes Alter hatten:
| Monate | Kinder |
|---|---|
 |  |
 |  |
 | |
 |  |
 | |
 |  |
 | |
Berechne den Modus.
In der Spalte für Kinder entspricht die höchste absolute Häufigkeit von dem Alter von Monaten. Der Modus 
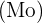ist in diesem Fall also
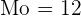
Berechne den Modus einer statistischen Verteilung, die durch folgende Tabelle gegeben ist:
| Intervall | Absolute Häufigkeit  |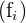
|---|---|
 | |
 |  |
 |  |
 |  |
 | |
 |
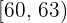Zunächst suchen wir das Intervall, in dem sich der Modus befindet, d. h. das Intervall mit der höchsten absoluten Frequenz 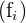, die beträgt. Die Modalklasse ist also
.
Wir wenden die Formel zur Berechnung des Modus für gruppierte Daten an und extrahieren die folgenden Daten:
Untergrenze 
Formel für den Modus:
Werte einsetzen:
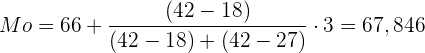
Der Modus ist:
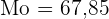
Berechne den Modus einer statistischen Verteilung, die durch folgende Tabelle gegeben ist:
| Intervall | |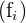
|---|---|
 |  |
 | |
 |  |
 | |
 |  |
Die größte absolute Häufigkeit 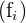ist . Die Modalklasse ist also
Wir wenden die Formel zur Berechnung des Modus für gruppierte Daten an und extrahieren die folgenden Daten:
Untergrenze 
Formel für den Modus:
Werte einsetzen:
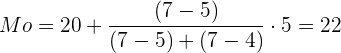
Der Modus ist somit
Berechne den Modus der statistischen Verteilung:
| Intervall | |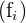
|---|---|
 | |
 | |
| |
| |
| |
 |  |
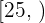Die größte absolute Häufigkeit 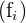ist . Die Modalklasse ist somit
Wir wenden die Formel zur Berechnung des Modus für gruppierte Daten an und extrahieren die folgenden Daten:
Untergrenze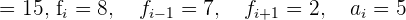 
Formel für den Modus:
Werte einsetzen:
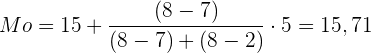
Der Modus ist somit
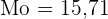
Das Histogramm der Verteilung, die dem Gewicht von 100 Abiturienten entspricht, sieht wie folgt aus
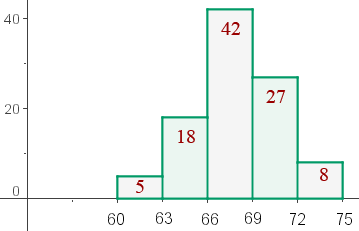
Berechne den Modus.
Die größte absolute Häufigkeit 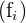ist . Die Modalklasse ist also
Wir wenden die Formel zur Berechnung des Modus für gruppierte Daten an und extrahieren die folgenden Werte:
Untergrenze 
Formel für den Modus:
Werte einsetzen:
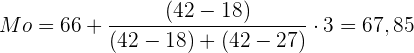
Der Modus ist somit
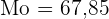
Die folgende Tabelle zeigt die Noten (nicht bestanden, bestanden, gut und hervorragend), die eine Gruppe von 50 Schüler:innen erhalten hat. Berechne den Modus.
| Intervall | |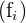
|---|---|
| |
 |  |
 | |
 | |
|
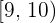Zunächst erstellen wir eine neue Spalte mit den Höhen, indem wir die absoluten Häufigkeiten durch die Breiten der entsprechenden Intervalle teilen
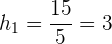
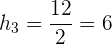
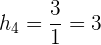
| Intervall | |  |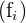
|---|---|---|
| | |
| | |
| | |
| | |
|
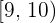Die Modalklasse ist , denn diese hat die größte Höhe von .
Wir wenden die Formel zur Berechnung des Modus für gruppierte Daten an und extrahieren die folgenden Daten:
Untergrenze 
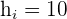
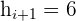
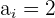
Formel für den Modus:
Werte einsetzen:
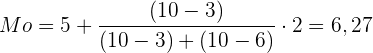
Der Modus ist somit
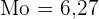
Berechne den Modus einer statistischen Verteilung, die durch folgende Tabelle gegeben ist:
| Intervall | Absolute Häufigkeit |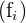
|---|---|
 | |
 |  |
 |  |
 |  |
 | |
|
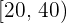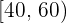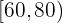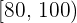Zunächst suchen wir das Intervall, in dem sich der Modus befindet, d. h. das Intervall mit der höchsten absoluten Häufigkeit 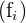, die beträgt. Die Modalklasse ist also
.
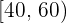Wir wenden die Formel zur Berechnung des Modus für gruppierte Daten an und extrahieren die folgenden Daten:
Untergrenze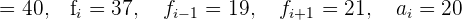 
Formel für den Modus:
Werte einsetzen:
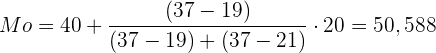
Der Modus ist somit:
Eine Baseballmannschaft erzielte in jedem der Durchgänge des Spiels die folgende Anzahl von Runs:
| Durchgänge | Runs |
|---|---|
| |
|  |
| |
| |
| |
| |
| |
| |
| |
Wir sehen uns die Spalte der Runs an und stellen fest, dass die am häufigsten wiederholte Anzahl der Runs ist, die in den Durchgängen 
und erzielt wurde. Der Modus ist also
Berechne den Modus der folgenden Menge an Zahlen.
Da alle Zahlen gleich häufig 
vorkommen, hat die Menge keinen Modus.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
