Kapitel
Ein statistischer Parameter ist eine Zahl, die aus den Daten einer statistischen Stichprobe gewonnen wird. Statistische Parameter werden auch als deskriptive (oder beschreibende) Statistik bezeichnet.
Statistische Parameter dienen dazu, die in einer Tabelle oder einem Diagramm enthaltenen Informationen zusammenzufassen. Mit anderen Worten: Mit einigen wenigen statistischen Parametern kann man sich ein allgemeines Bild von der Verteilung der Daten machen.
Die statistischen Parameter liefern eine gute Zusammenfassung, wenn die Verteilung der Grundgesamtheit bekannt ist. Insbesondere wenn die Stichprobe aus einer Normalverteilung stammt, geben der Standardmittelwert und die Standardabweichung eine gute Zusammenfassung der Verteilung.
Beispiele für statistische Parameter sind der Mittelwert, der Median, die Standardabweichung und die Quartile.
Die statistischen Parameter werden nach den Informationen klassifiziert, die sie zusammenfassen. Die beiden häufigsten Arten von statistischen Parametern sind:
- Lagemaß oder Lageparameter
- Streuungsmaß
Andere Arten von statistischen Parametern sind Form- und Skalenparameter. Diese Parameter werden üblicherweise in Verteilungen wie Beta, Pareto oder Weibull verwendet – daher werden wir sie nicht beschreiben, da wir uns hauptsächlich auf die Normalverteilung konzentrieren.
Lageparameter
Diese Parameter geben an, um welchen Wert (Zentrum) die Daten verteilt sind.
Einige Lageparameter sind (klicke auf den Link, um eine detaillierte Beschreibung der einzelnen Parameter zu sehen):
Arithmetisches Mittel:
Der Mittelwert ist der Durchschnittswert der Stichprobe. Er kann auch als Schwerpunkt der Daten interpretiert werden.
Median:
Der Median ist der Wert, der die obere Hälfte der Stichprobe von der unteren Hälfte trennt. Mit anderen Worten: Er teilt die Daten in zwei gleiche Teile.
Modus:
Der Modus ist der sich am häufigsten wiederholende Wert in einer Stichprobe. Das heißt, er ist der häufigste Wert.
Beispiel
Wir haben die folgenden Daten, die das Alter der Mitarbeitenden eines Büros darstellen:
Für diese Daten gilt:
1 Der Mittelwert liegt bei 29,92 Jahren. Das heißt, das Durchschnittsalter der Mitarbeitenden beträgt 30 Jahre (nach Rundung).
2 Der Modus dieser Daten ist 27 Jahre. Daher ist das Alter von 27 Jahren das häufigste.
3 Der Median ist ebenfalls mediana es 27 Jahre. Das bedeutet, dass die Hälfte der Beschäftigten über 27 Jahre alt ist, während die andere Hälfte 27 Jahre alt oder jünger ist.
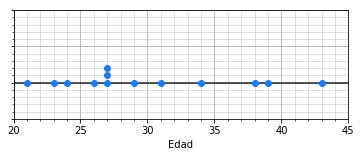
Die Daten sind in der folgenden Grafik dargestellt:
Streuungsmaße
Streuungsmaße sagen uns, wie weit die Werte der Verteilung vom Zentrum entfernt sind. Das heißt, sie sind eine Zusammenfassung dessen, wie gestreut die Daten sind.
Einige Streuungsmaße sind:
Spannweite:
Die Spannweite ist die Differenz zwischen dem größten und dem kleinsten Wert in einer Stichprobe. Dieser Wert sagt uns, in welcher Spannweite die Daten liegen.
Mittelere absolute Abweichung:
Die mittlere absolute Abweichung ist der Mittelwert aus den absoluten Werten der Abweichungen vom Mittelwert. Mit anderen Worten, es handelt sich um den Durchschnitt der Abweichung der Daten vom Mittelwert.
Varianz:
Die Varianz ist der Durchschnitt des Quadrats der Abweichungen vom Mittelwert. Mit anderen Worten, sie misst die durchschnittliche Abweichung der Daten vom Mittelwert zum Quadrat – zuerst wird quadriert und dann der Durchschnitt berechnet.
Standardabweichung:
Die Standardabweichung ist die Quadratwurzel der Varianz. Sie ist in der Regel ein besserer Schätzwert als die mittlere Abweichung, wenn es sich um eine Normalverteilung handelt.
Quantile:
Quantile teilen eine Stichprobe in cuantiles dividen una muestra en 
gleiche Teile. Diese helfen uns, eine Vorstellung von den Spannweiten zu bekommen, in denen sich die meisten Werte konzentrieren.
Abhängig vom Wert für können Quantile bestimmte Namen haben:
- Quartile: Diese teilen die Daten in vier gleiche Teile.
- Dezile: Diese teilen die Stichprobe in zehn gleich große Mengen.
- Perzentile: Diese teilen die Daten in 100 gleiche Teile.
Beispiel
Mit den gleichen Daten wie im vorherigen Beispiel – Alter der Mitarbeitenden in einem Büro:
Die Streuungsmaße dieser Daten sind:
1 Die Spannweite ist 22 Jahre. Das heißt, dass zwischen dem/der jüngsten und dem/der ältesten Arbeitnehmenden ein Unterschied von 22 Jahren besteht.
2 Die mittlere absolute Abweichung ist 5,44 Jahre. Das heißt, die Beschäftigten sind tendenziell 5 Jahre jünger oder älter als der Durchschnitt - diese Abweichung ist ein Durchschnittswert, so dass einige Beschäftigte um mehr als 5 Jahre und andere um weniger als 5 Jahre abweichen.
3 Die Varianz ist 41,61 Jahre.
4 Die Standardabweichung liegt bei 6,45 Jahren.
5 Schließlich umfasst die Stichprobe nur 13 Personen. Aus diesem Grund ist es nicht sinnvoll, Dezile oder Perzentile zu ermitteln. Wir können jedoch Quartile berechnen:
- 1. Quartil: 26 Jahre.
- 2. Quartil: 27 Jahre.
- 3. Quartil: 34 Jahre.
Daraus lässt sich schließen, dass etwa 25 % der Beschäftigten unter 26 Jahre alt sind. Darüber hinaus gibt es viele Beschäftigte zwischen 26 und 27 Jahren (fast 25 % der Beschäftigten liegen zwischen diesem Alter, da sie zwischen dem ersten und zweiten Quartil liegen). Schließlich sind nur 25 % der Beschäftigten über 34 Jahre alt - was bedeutet, dass etwa 75 % der Beschäftigten unter 34 Jahre alt sind.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
