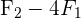Kapitel
Was ist der Rang einer Matrix
Es gibt mehrere gleichwertige Definitionen für den Rang einer Matrix. Den Rang einer Matrix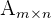 
der Dimension 
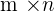benennen wir mit 
, 
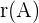oder im Englischen mit 
.
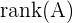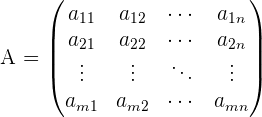
Dimension des Spalten- oder Zeilenraums
In der Technik ist es vielleicht am gebräuchlichsten, den Rang als die Anzahl der linear unabhängigen Zeilen (oder Spalten) zu definieren, weil es einfach ist, die linear unabhängigen Zeilen einer Matrix mit dem Gauß-Verfahren oder der Gauß-Jordan-Methode zu ermitteln.
Beispiel:
Wir sehen uns die Matrix 
an, die wie folgt gegeben ist
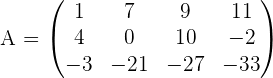
Wir stellen fest, dass die 1. Zeile 
und die 2. Zeile 
linear unabhängig sind, da
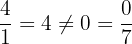
Jedoch sind die 1. und 3. Zeile embargo, la primer fila y la tercer fila, linear unabhängig, da 
. Wir haben also zwei linear unabhängige Zeilen der drei Zeilen, aus denen die Matrix besteht. Somit ist der Rang von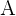 
: 
.
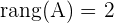Beispiel:
Nun wenden wir das Gauß-Verfahren an, um den Rang der Matrix aus dem vorherigen Beispiel zu ermitteln.
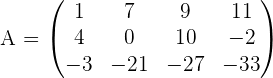
Mit dem Gauß-Verfahren erhalten wir
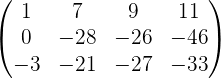
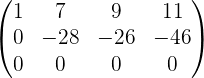
Am Ende unseres Prozesses ergibt sich die folgende Matrix
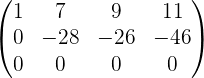
Da wir am Ende zwei Zeilen haben, die nicht 0 sind, ist der Rang .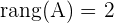
Rang nach Determinanten
Wir können den Rang einer Matrix als die Ordnung der größten quadratischen Untermatrix unserer Matrix definieren, die nicht 0 ist. Mit dieser Definition ist es möglich, den Rang mithilfe von Determinanten zu berechnen. Dies ist jedoch keine sehr empfehlenswerte Methode, da die Berechnung einiger Determinanten zu zeitaufwendig und je nach Dimension der Matrix sogar sehr kompliziert sein kann.
Beispiel:
Wir sehen uns die folgende Matrix an
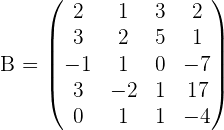
Wir fahren mit den einzelnen Schritten fort:
1 Wir streichen die dritte Spalte, weil sie eine lineare Kombination der ersten beiden Spalten ist,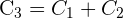 
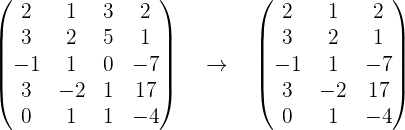
2 Wir prüfen, ob sie einen Rang größer oder gleich 1 hat. Dazu muss mindestens ein Element der Matrix ungleich 0 sein, so dass ihre Determinante nicht 0 ist. Da die Matrix nicht 0 ist, haben wir
.
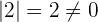Daher ist ihr Rang gleich oder größer als 1.
3 Sie hat den Rang größer oder gleich 2, wenn es eine beliebige quadratische Untermatrix der Ordnung 2 gibt, deren Determinante nicht 0 ist:
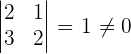
4 Sie hat den Rang größer oder gleich 3, wenn es eine beliebige quadratische Untermatrix der Ordnung 3 gibt, so dass ihre Determinante nicht 0 ist. Berechnet man in diesem Fall die Determinanten aller Untermatrizen der Dimension 3, so ergibt sich, dass
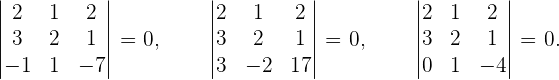
Da alle Determinanten der Untermatrizen 0 sind, haben sie einen Rang kleiner als 3, also 
.
Dimension des Bildraums
Diese Definition des Rangs einer Matrix ist etwas mathematischer und komplizierter, allerdings ist es nicht schlecht, sie zu kennen. Hier müssen wir uns des Konzepts der linearen Anwendungen bewusst sein. Das liegt daran, dass es nach der Theorie der linearen Algebra für eine Matrix 
nur eine zugehörige lineare Anwendung gibt:
,
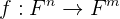definiert als
,
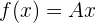Der Rang von 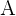ist somit die Dimension des Bildes von 
(als Vektorraum).
Es ist nicht notwendig, diese Definition zu beherrschen, da sie normalerweise nur in der reinen Mathematik oder Physik zur Anwendung kommt, aber sie kann als eine allgemeine Tatsache betrachtet werden.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
