Kapitel
- Definitionsmenge von Polynomfunktionen
- Definitionsmenge von rationalen Funktionen
- Definitionsmenge von Wurzelfunktionen
- Definitionsmenge von Exponentialfunktionen
- Definitionsmenge von Logarithmusfunktionen
- Definitionsmenge von trigonometrischen Funktionen
- Symmetrie von Funktionen
- Monotonieverhalten von Funktionen
- Umkehrfunktion
- Verkettung von Funktionen
- Verkettung von trigonometrischen Funktionen

Definitionsmenge von Polynomfunktionen
Berechne die Definitionsmenge der Polynomfunktionen


Die Definitionsmenge einer Polynomfunktion ist 



Diese Funktion ist auch eine Polynomfunktion, da kein x im Nenner steht. Sie kann wie folgt geschrieben werden:

Ihre Definitionsmenge ist also 

Definitionsmenge von rationalen Funktionen

Die Definitionsmenge einer rationalen Funktion ist  minus die Werte, für die der Nenner null wird.
minus die Werte, für die der Nenner null wird.

Wir müssen den Nenner 0 setzen und die Gleichung lösen.


Die Lösungen der Gleichung sind die Punkte, die nicht zur Definitionsmenge gehören, da durch sie der Nenner 0 wird.



Wir setzen den Nenner gleich 0 und lösen die Gleichung.



Die Lösungen der Gleichung sind die Punkte, die nicht zur Definitionsmenge gehören, da durch sie der Nenner 0 wird.



Wir setzen den Nenner gleich 0 und lösen die Gleichung.


Da die Gleichung keine Lösungen hat, wird der Nenner nicht durch eine reelle Zahl 0.



Wir setzen den Nenner gleich 0 und lösen die Gleichung.




Da diese Gleichung eine doppelte Nullstelle hat, ist das einzige Element, das nicht zur Definitionsmenge gehört, -1.



Wir setzen den Nenner gleich 0 und lösen die Gleichung.
Wir stellen fest, dass das Polynom ein Binom hoch 3 ist.

Da diese Gleichung eine dreifache Nullstelle hat, ist das einzige Element, das nicht zur Definitionsmenge gehört,  .
.

Definitionsmenge von Wurzelfunktionen
Die Definitionsmenge einer Wurzelfunktion mit geradem Wurzelexponenten besteht aus der Menge der Werte, bei denen der Radikand größer oder gleich Null ist.


Wir setzen den Radikanden größer oder gleich 0 und lösen die Ungleichung


Die Werte der Definitionsmenge müssen also größer oder gleich 2 sein




Wir multiplizieren die Ungleichung mit –1 und das Vorzeichen der Ungleichung ändert sich


Die Werte der Definitionsmenge müssen also kleiner oder gleich 2 sein




Wir setzen gleich 0, um die Nullstellen der Gleichung zu ermitteln.

Wir lösen die Gleichung durch Faktorisieren oder mithilfe der Mitternachtsformel. Die Nullstellen sind  und
und  .
.
Die Nullstellen teilen die Zahlengerade in 3 Intervalle:  .
.
Wir analysieren die Positiviät oder Negativität von  in diesen Intervallen. Dazu nehmen Sie einfach jeweils einen Punkt. Wir kommen zu folgendem Schluss:
in diesen Intervallen. Dazu nehmen Sie einfach jeweils einen Punkt. Wir kommen zu folgendem Schluss:
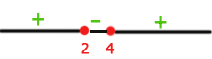
Sie muss größer (wir nehmen die Intervalle mit dem Vorzeichen +) oder gleich 0 sein (wir nehmen als Lösung die Extremwerte der Intervalle).




Wir multiplizieren mit –1 und ändern das Vorzeichen der Ungleichung

Wir lösen die Gleichung und die Nullstellen sind 2 und 4
Wir nehmen das negative Intervall als Lösung an, weil wir jetzt kleiner als oder gleich 0 haben.
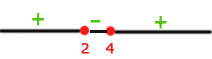



Diese Gleichung hat eine doppelte Nullstelle:  wird als Binom zum Quadrat faktorisiert.
wird als Binom zum Quadrat faktorisiert.


Da sie größer oder gleich 0 ist, und auch jede Zahl zum Quadrat positiv oder 0 ist, ist die Definitonsmenge 



Wenn wir gleich 0 setzen, hat die entsprechende Gleichung keine reellen Lösungen.
Wenn wir einen beliebigen Wert nehmen, ist sie positiv.






Ein Binom zum Quadrat ist immer positiv, aber da wir das Vorzeichen vorangestellt haben, ist sie stets negativ.
Wir finden nur eine Lösung mit  , da hierfür die Gleichung 0 wird
, da hierfür die Gleichung 0 wird





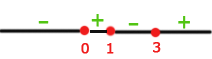
Wir nehmen die positiven Intervalle und die Nullstellen


Die Nullstellen sind 1, 3 und 0. Dies teilt die Zahlegerade in folgende Intervalle:


Da die Wurzel im Nenner steht, muss der Radikand größer als 0 sein, darf aber nicht gleich sein, da er sonst den Nenner aufheben würde.




In diesem Fall muss der Nenner ungleich 0 sein und die Wurzel des Zählers muss größer oder gleich 0 sein.
Die Lösung ist die Schnittmenge der beiden Mengen



Da es sich um eine Wurzel mit ungeradem Wurzelexponenten handelt, ist der einzige Punkt, der nicht zur Definitionsmengegehört,  , da so der Nenner 0 wird.
, da so der Nenner 0 wird.

Definitionsmenge von Exponentialfunktionen
Berechne die Definitionsmenge der folgenden Exponentialfunktionen:
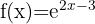
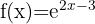
Die Definitionsmenge einer Exponentialfunktion ist 



Da der Exponent rational ist, gehört  nicht zur Definitionsmenge, da es den Nenner aufhebt.
nicht zur Definitionsmenge, da es den Nenner aufhebt.

Definitionsmenge von Logarithmusfunktionen


Damit der Logarithmus existiert, muss die Funktion größer als 0 sein.



Da der Nenner immer positiv ist, sehen wir und nur den Zähler an.

Definitionsmenge von trigonometrischen Funktionen
Berechne die Definitionsmenge der folgenden trigonometrischen Funktionen:


Der Sinuswert befindet sich zwischen  und
und  . Somit ist
. Somit ist  immer kleiner oder gleich
immer kleiner oder gleich  .
.





Der Kosinuswert ist immer kleiner oder gleich  . Somit ist
. Somit ist

Symmetrie von Funktionen
Untersuche die Symmetrie der folgenden Funktionen:



Symmetrie zu den Ordinatenachsen. Gerade Funktion.



Symmetrie zum Ursprung. Ungerade Funktion.


 .
.
Symmetrie zum Ursprung. Ungerade Funktion.



Symmetrie zu den Ordinatenachsen. Gerade Funktion.
Monotonieverhalten von Funktionen
Untersuche das Monotonieverhalten der folgenden Funktionen
 bei
bei 
 bei
bei 
Wir nehmen eine Steigung, 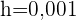 , am Punkt
, am Punkt  .
.
Die Funktion steigt oder fällt am Punkt  , wenn sie im Intervall
, wenn sie im Intervall 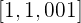 steigt oder fällt
steigt oder fällt
Um dies zu überprüfen, berechnen wir die Änderungsrate im gegebenen Intervall:
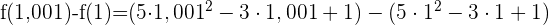
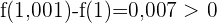
Die Funktion steigt bei 
 bei
bei 
 bei
bei 
Wir nehmen eine Steigung, 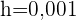 , am Punkt
, am Punkt  .
.
Die Funktion steigt oder fällt am Punkt  , wenn sie im Intervall
, wenn sie im Intervall 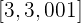 steigt oder fällt.
steigt oder fällt.
Um dies zu überprüfen, berechnen wir die Änderungsrate im gegebenen Intervall:
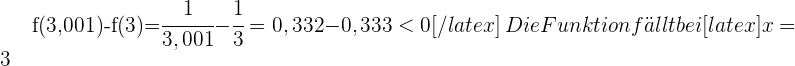
Umkehrfunktion
Bestimme die Umkehrfunktionen von


Wir schreiben die Funktion mit  und
und 
Wir bestimmen die Variable  in Funktion der Variablen
in Funktion der Variablen 


Wir tauschen die Variablen



Wir bestimmen die Variable  in Funktion der Variablen
in Funktion der Variablen 



Wir tauschen die Variablen



Wir eliminieren die Nenner


Wir eliminieren die Klammer und klammern den gemeinsamen Faktor  aus. Schließlich tauschen wir die Variablen
aus. Schließlich tauschen wir die Variablen

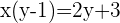

Wir tauschen die Variablen



Wir bestimmen die Variable  in Funktion der Variablen
in Funktion der Variablen 


Wir tauschen die Variablen

Es handelt sich nicht um eine Funktion. Es existiert keine Umkehrfunktion, da jedes Element zwei Abbildungen hat und eine Funktion höchstens eine Abbildung haben kann.
Verkettung von Funktionen
Gegeben sind die Funktionen:

Berechne:


































Beweise, dass: 
Beweise, dass: 

Tatsächlich ist  die identische Abbildung
die identische Abbildung
Verkettung von trigonometrischen Funktionen
Gegeben sind die Funktionen:

Berechne:






Mit KI zusammenfassen:












