
Schnittpunkte mit den Achsen
Ein Schnittpunkt einer Funktion mit einer der Achsen ist ein Punkt, an dem die Funktion
die Achse schneidet. Um diese Punkte zu ermitteln, müssen wir die Funktion gleich 0 setzen, um den Schnittpunkt mit der x-Achse zu bestimmen und
 nehmen, um den Schnittpunkt mit der
nehmen, um den Schnittpunkt mit der
y-Achse zu finden .
Berechnung der Schnittpunkte
Bestimme die Schnittpunkte der Funktion 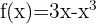 mit der x-Achse und der y-Achse.
mit der x-Achse und der y-Achse.
Schnittpunkte mit der x-Achse: In diesem Fall müssen wir die Funktion  gleich 0 setzen und den Wert für
gleich 0 setzen und den Wert für  bestimmen
bestimmen 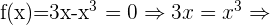
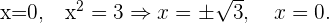
Mit diesen Werten von  sind die Schnittpunkte
sind die Schnittpunkte
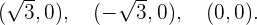
Schnittpunkte mit der y-Achse:
In diesem Fall müssen wir  gleich 0 setzen und sehen, welchen Wert die Funktion hat
gleich 0 setzen und sehen, welchen Wert die Funktion hat
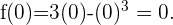
Mit diesem Wert lautet der Schnittpunkt

Bestimme die Schnittpunkte der Funktion 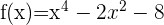 mit der x-Achse und der y-Achse.
mit der x-Achse und der y-Achse.
Schnittpunkte mit der x-Achse: In diesem Fall müssen wir die Funktion  gleich 0 setzen und den Wert für
gleich 0 setzen und den Wert für  bestimmen
bestimmen 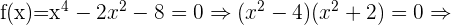
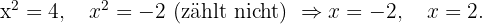
Mit diesen Werten von  sind die Schnittpunkte
sind die Schnittpunkte

Schnittpunkte mit der y-Achse:
In diesem Fall müssen wir  gleich 0 setzen und sehen, welchen Wert die Funktion hat
gleich 0 setzen und sehen, welchen Wert die Funktion hat
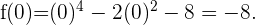
Mit diesem Wert lautet der Schnittpunkt
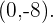
Bestimme die Schnittpunkte der Funktion 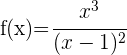 mit der x-Achse und der y-Achse.
mit der x-Achse und der y-Achse.
Schnittpunkte mit der x-Achse: In diesem Fall müssen wir die Funktion  gleich 0 setzen und den Wert von
gleich 0 setzen und den Wert von  ermitteln
ermitteln 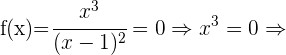
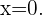
Mit diesem Wert von  ist der Schnittpunkt
ist der Schnittpunkt

Schnittpunkte mit der y-Achse:
In diesem Fall müssen wir  gleich 0 setzen und sehen, welchen Wert die Funktion hat
gleich 0 setzen und sehen, welchen Wert die Funktion hat
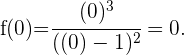
Mit diesem Wert lautet der Schnittpunkt

Bestimme die Schnittpunkte der Funktion 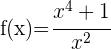 mit der x-Achse und der y-Achse.
mit der x-Achse und der y-Achse.
Schnittpunkte mit der x-Achse: EIn diesem Fall müssen wir die Funktion  gleich 0 setzen und den Wert für
gleich 0 setzen und den Wert für  bestimmen
bestimmen 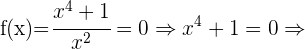
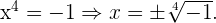
Da wir eine negative gerade Nullstelle haben, folgern wir daraus, dass
es keine Schnittpunkte gibt.
Schnittpunkte mit der y-Achse:
In diesem Fall müssen wir  gleich 0 setzen und sehen, welchen Wert die Funktion hat
gleich 0 setzen und sehen, welchen Wert die Funktion hat

Da der Nenner gleich 0 ist, haben wir keinen Wert für die
Funktion und können daraus schließen, dass es keine Schnittpunkte gibt.
Bestimme die Schnittpunkte der Funktion  mit der x-Achse und der y-Achse.
mit der x-Achse und der y-Achse.
Schnittpunkte mit der x-Achse: In diesem Fall müssen wir die Funktion  gleich 0 setzen und den Wert für
gleich 0 setzen und den Wert für  bestimmen
bestimmen 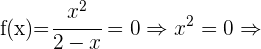
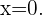
Mit diesem Wert von  ist der Schnittpunkt
ist der Schnittpunkt

Schnittpunkte mit der y-Achse:
In diesem Fall müssen wir  gleich 0 setzen und sehen, welchen Wert die Funktion hat
gleich 0 setzen und sehen, welchen Wert die Funktion hat
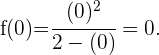
Mit diesem Wert lautet der Schnittpunkt

Bestimme die Schnittpunkte der Funktion 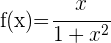 mit der x-Achse und der y-Achse.
mit der x-Achse und der y-Achse.
Schnittpunkte mit der x-Achse: In diesem Fall müssen wir die Funktion  gleich 0 setzen und den Wert für
gleich 0 setzen und den Wert für  bestimmen
bestimmen 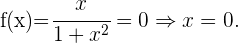 Mit diesem Wert von
Mit diesem Wert von  ist der Schnittpunkt
ist der Schnittpunkt

Schnittpunkte mit der y-Achse:
In diesem Fall müssen wir  gleich 0 setzen und sehen, welchen Wert die Funktion hat
gleich 0 setzen und sehen, welchen Wert die Funktion hat
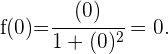
Mit diesem Wert lautet der Schnittpunkt

Bestimme die Schnittpunkte der Funktion  mit der x-Achse und der y-Achse.
mit der x-Achse und der y-Achse.
Schnittpunkte mit der x-Achse: In diesem Fall müssen wir die Funktion  gleich 0 setzen und den Wert für
gleich 0 setzen und den Wert für  bestimmen
bestimmen 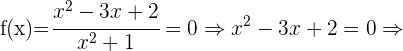
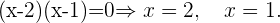
Mit diesen Werten lauten die Schnittpunkte

Schnittpunkte mit der y-Achse:
In diesem Fall müssen wir  gleich 0 setzen und sehen, welchen Wert die Funktion hat
gleich 0 setzen und sehen, welchen Wert die Funktion hat
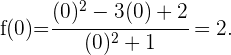
Mit diesem Wert lautet der Schnittpunkt

Bestimme die Schnittpunkte der Funktion  mit der x-Achse und der y-Achse.
mit der x-Achse und der y-Achse.
Schnittpunkte mit der x-Achse:In diesem Fall müssen wir die Funktion  gleich 0 setzen und den Wert für
gleich 0 setzen und den Wert für  bestimmen
bestimmen 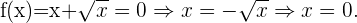 Mit diesem Wert von
Mit diesem Wert von  ist der Schnittpunkt
ist der Schnittpunkt

Schnittpunkte mit der y-Achse:
In diesem Fall müssen wir  gleich 0 setzen und sehen, welchen Wert die Funktion hat
gleich 0 setzen und sehen, welchen Wert die Funktion hat
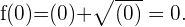
Mit diesem Wert lautet der Schnittpunkt

Bestimme die Schnittpunkte der Funktion 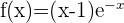 mit der x-Achse und der y-Achse.
mit der x-Achse und der y-Achse.
Schnittpunkte mit der x-Achse:In diesem Fall müssen wir die Funktion  gleich 0 setzen und den Wert für
gleich 0 setzen und den Wert für  bestimmen
bestimmen 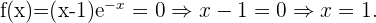 Mit diesem Wert von
Mit diesem Wert von  ist der Schnittpunkt
ist der Schnittpunkt
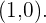
Schnittpunkte mit der y-Achse:
In diesem Fall müssen wir  gleich 0 setzen und sehen, welchen Wert die Funktion hat
gleich 0 setzen und sehen, welchen Wert die Funktion hat
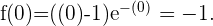
Mit diesem Wert lautet der Schnittpunkt
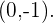
Bestimme die Schnittpunkte der Funktion 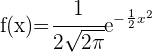 mit der x-Achse und der y-Achse.
mit der x-Achse und der y-Achse.
Schnittpunkte mit der x-Achse:In diesem Fall müssen wir die Funktion  gleich 0 setzen und den Wert für
gleich 0 setzen und den Wert für  bestimmen
bestimmen  Da die Exponentialfunktion nicht 0 wird, können wir sagen, dass
Da die Exponentialfunktion nicht 0 wird, können wir sagen, dass
es keinen Schnittpunkt gibt.
Schnittpunkte mit der y-Achse:
In diesem Fall müssen wir  gleich 0 setzen und sehen, welchen Wert die Funktion hat
gleich 0 setzen und sehen, welchen Wert die Funktion hat
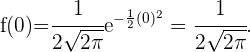
Mit diesem Wert lautet der Schnittpunkt
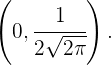
Bestimme die Schnittpunkte der Funktion 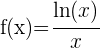 mit der x-Achse und der y-Achse.
mit der x-Achse und der y-Achse.
Schnittpunkte mit der x-Achse: In diesem Fall müssen wir die Funktion  gleich 0 setzen und den Wert für
gleich 0 setzen und den Wert für  bestimmen
bestimmen
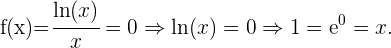 Mit diesem Wert von
Mit diesem Wert von  ist der Schnittpunkt
ist der Schnittpunkt
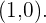
Schnittpunkte mit der y-Achse:
In diesem Fall müssen wir  gleich 0 setzen und sehen, welchen Wert die Funktion hat
gleich 0 setzen und sehen, welchen Wert die Funktion hat

Da der Nenner gleich 0 ist und der Logarithmus von 0 nicht existiert, können wir daraus schließen, dass es keinen Schnittpunkt gibt.












