Kapitel
Die Standardabweichung ist die Quadratwurzel der Varianz.
Das heißt, die Quadratwurzel aus dem Mittelwert der Abweichungswerte zum Quadrat.
Die Standardabweichung wird dargestellt durch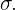 
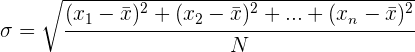
Beispiel
Berechne die Standardabweichung der Verteilung:
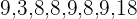
Wir berechnen das arithmetische Mittel
Wir setzen in die Formel der Standardabweichung ein
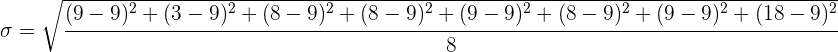
Standardabweichung für gruppierte Daten
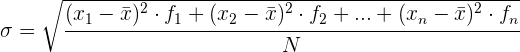
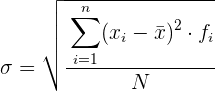
Um die Berechnung zu vereinfachen, verwenden wir die folgenden Ausdrücke, die äquivalent zu den vorherigen sind.
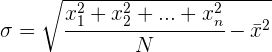
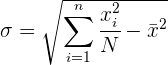
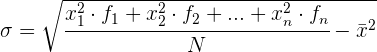
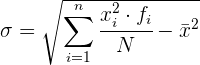
Beispiel
Berechne die Standardabweichung der Verteilung der folgenden Tabelle:
 |  |  |  | |
|---|---|---|---|---|
 |  |  | |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  | |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |
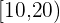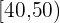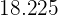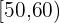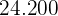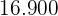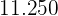Wir haben die Spalte hinzugefügt, da wir deren Summe 
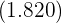ermitteln möchten, die wir im Anschluss durch 
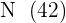dividieren, um so den Mittelwert zu berechnen
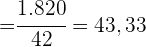
Wir haben die Spalte hinzugefügt, da wir deren Summe 
ermitteln möchten, die wir im Anschluss durch 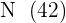dividieren. Vom Ergebnis subtrahieren wir das arithmetische Mittel zum Quadrat 
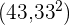. Zum Schluss ziehen wir die Quadratwurzel aus dem erhaltenen Ergebnis
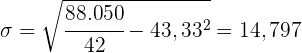
Eigenschaften der Standardabweichung
1 Die Standardabweichung ist immer ein positiver Wert oder null, wenn alle Werte gleich sind.
2 Wenn zu allen Werten der Variablen eine Zahl addiert wird, ändert sich die Standardabweichung nicht.
3 Wenn alle Werte der Variablen mit einer Zahl multipliziert werden, wird die Standardabweichung mit dieser Zahl multipliziert.
4 Wenn wir mehrere Verteilungen mit demselben Mittelwert haben und ihre jeweiligen Standardabweichungen bekannt sind, kann die Gesamtstandardabweichung berechnet werden.
Wenn alle Stichproben gleich groß sind:
Wenn die Stichproben unterschiedlich groß sind:
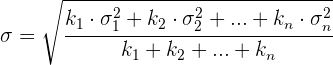
Beobachtungen zur Standardabweichung
1 Die Standardabweichung ist ebenso wie der Mittelwert und die Varianz ein sehr empfindlicher Indikator für die Extremwerte.
2 In Fällen, in denen der Mittelwert nicht ermittelt werden kann, ist es auch nicht möglich, die Standardabweichung zu bestimmen.
3 Je kleiner die Standardabweichung ist, desto größer ist die Konzentration der Daten um den Mittelwert.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
