Kapitel
Die Statistik befasst sich mit dem Zählen, Sortieren und Klassifizieren von Daten, die aus Beobachtungen gewonnen werden, um Vergleiche anstellen und Schlussfolgerungen ziehen zu können.

Konzepte der Statistik
Grundgesamtheit
Eine Grundgesamtheit ist die Menge aller Elemente, die Gegenstand einer statistischen Untersuchung sind.
Statistische Einheit
Eine statistische Einheit ist jedes der Elemente, aus denen sich die Grundgesamtheit zusammensetzt.
Stichprobe
Eine Stichprobe ist ein repräsentativer Satz der Referenzgrundgesamtheit. Die Anzahl der Einheiten in einer Stichprobe ist kleiner als die Anzahl der Einheiten in der Grundgesamtheit.
Probenahme
Bei der Probenahme werden die zu untersuchenden Daten aus einem kleinen, repräsentativen Teil der Grundgesamtheit erhoben.
Wert
Ein Wert ist jedes der verschiedenen Ergebnisse, die in einer statistischen Studie erzielt werden können. Wenn wir 5 Mal eine Münze werfen, erhalten wir zwei Werte: Kopf und Zahl.
Datenwert
Ein Datenwert ist jeder der aus einer statistischen Studie gewonnenen Werte. Wenn wir fünfmal eine Münze werfen, erhalten wir fünf Daten: Kopf, Kopf, Zahl, Kopf, Zahl.
Statistische Variablen
Es gibt zwei Arten von statistischen Variablen: qualitative und quantitative
Qualitative Variable
Qualitative Variablen beziehen sich auf Merkmale oder Eigenschaften, die nicht mit Zahlen gemessen werden können. Wir können zwei Arten unterscheiden:
Nominalskalierte Variable
Eine nominalskalierte Variable weist nichtnumerische Modi auf, die keiner Rangfolge unterliegen.
Ordinalskalierte Variable
Eine ordinalskalierte Variable weist nichtnumerische Modi auf, die einer Rangfolge unterliegen.
Quantitative Variable
Eine quantitative Variable ist eine Variable, die als Zahl ausgedrückt wird und mit der daher arithmetische Operationen durchgeführt werden können. Wir können zwischen zwei Arten unterscheiden:
Diskrete Variable
Eine diskrete Variable ist eine Variable, die nur eine endliche Anzahl von Werten zwischen zwei beliebigen Werten eines Merkmals annehmen kann.
Stetige Variable
Eine stetige Variable ist eine Variable, die eine unendliche Anzahl von Werten zwischen zwei beliebigen Werten eines Merkmals annehmen kann.
Häufigkeitsverteilung
Die Häufigkeitsverteilung oder Häufigkeitstabelle ist eine tabellarische Anordnung statistischer Daten, bei der jedem Datenelement die entsprechende Häufigkeit zugewiesen wird.
Säulendiagramm
Ein Säulendiagramm wird verwendet, um qualitative Daten oder diskrete quantitative Daten darzustellen.
Die Daten werden durch Säulen dargestellt, deren Höhe proportional zur Häufigkeit ist.
Häufigkeitspolygon
Ein Häufigkeitspolygon wird gebildet, indem die Enden der Balken mit Segmenten verbunden werden.
Man kann auch die Punkte, die die Häufigkeiten repräsentieren, aufzeichnen und sie mit Segmenten verbinden.
Kreisdiagramm
Ein Kreisdiagramm kann für alle Arten von Variablen verwendet werden, wird aber häufig für qualitative Variablen eingesetzt.
Die Daten werden in einem Kreis dargestellt, so dass der Winkel jedes Segments proportional zu der entsprechenden absoluten Häufigkeit ist.
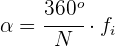
Histogramm
Ein Histogramm ist eine grafische Darstellung einer Variablen in Form von Balken.
Sie werden für stetige Variablen oder für diskrete Variablen mit einer großen Anzahl von Daten verwendet, die in Klassen gruppiert wurden.
Auf der x-Achse werden Rechtecke mit der Breite des Intervalls als Basis und der absoluten Häufigkeit der einzelnen Intervalle als Höhe konstruiert.
Maße zur Zentralisierung
Modus
Der Modus ist der Wert mit der höchsten absoluten Häufigkeit. Er wird dargestellt durch 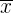
 und kann für qualitative und quantitative Variablen ermittelt werden.
und kann für qualitative und quantitative Variablen ermittelt werden.
Berechnung des Modus für gruppierte Daten
1 Alle Intervalle haben die gleiche Breite.
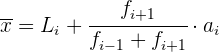
2 Die Intervalle haben unterschiedliche Breiten.
Zuerst müssen wir die Höhen bestimmen.
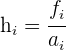
Die modale Klasse ist diejenige mit der größten Höhe.
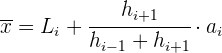
Median
Es ist der Wert, der den zentralen Platz aller Daten einnimmt, wenn sie vom kleinsten zum größten Wert geordnet werden. Der Median wird dargestellt durch 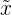 und kann nur für quantitative Variablen ermittelt werden.
und kann nur für quantitative Variablen ermittelt werden.
Berechnung des Medians
1 Wir ordnen die Daten vom kleinsten zum größten Wert.
2 Wenn die Reihe eine ungerade Anzahl von Messwerten hat, ist der Median der zentrale Wert der Reihe.
3 Wenn die Reihe eine gerade Anzahl von Werten hat, ist der Median der Mittelwert zwischen den beiden zentralen Werten.
Berechnung des Medians für gruppierte Daten
Der Median wird in dem Intervall gefunden, in dem die kumulierte Häufigkeit die Hälfte der Summe der absoluten Häufigkeiten erreicht, d. h. wir müssen das Intervall suchen, in dem sich 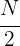 befindet.
befindet.
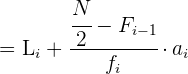
Arithmetisches Mittel
Das arithmetische Mittel ist der Wert, der sich aus der Addition aller Daten und der Division des Ergebnisses durch die Gesamtzahl der Daten ergibt. Es wird wie folgt dargestellt 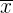
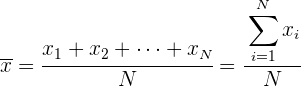
Arithmetisches Mittel für gruppierte Daten
Wenn die Daten in einer Häufigkeitstabelle gruppiert sind, lautet der Ausdruck für den Mittelwert:

Lagemaße
Quartile
Quartile sind die drei Werte der Variablen, die eine Menge von geordneten Daten in vier gleiche Teile unterteilen.  und
und  bestimmen die Werte, die
bestimmen die Werte, die 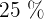 ,
, 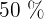 und
und  der Daten entsprechen.
der Daten entsprechen.

Dezile
Dezile sind die neun Werte, die eine Datenreihe in zehn gleiche Teile unterteilen. Sie geben die Werte an, die  ,
,  und
und  der Daten entsprechen.
der Daten entsprechen.
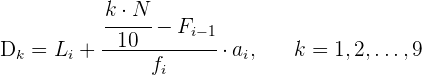
Perzentile
Perzentile sind die 99 Werte, die eine Datenreihe in 100 gleiche Teile unterteilen. Sie geben die Werte an, die  ,
, 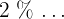
 der Daten entsprechen.
der Daten entsprechen.
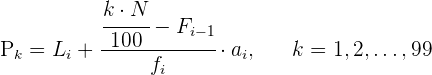
Streuungsmaße
Streuungsmaße geben an, wie weit die Werte der Verteilung vom Zentrum entfernt sind. Die Streuungsmaße sind:
Spannweite
Die Spannweite ist die Differenz zwischen dem größten und dem kleinsten Wert in einer statistischen Verteilung.
Mittlere absolute Abweichung
Die mittlere absolute Abweichung ist die Differenz zwischen jedem Wert der statistischen Variablen und dem arithmetischen Mittel.
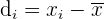
Die mittlere absolute Abweichung ist das arithmetische Mittel der absoluten Werte der Abweichungen vom Mittelwert.
Die mittlere absolute Abweichung wird mit 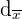
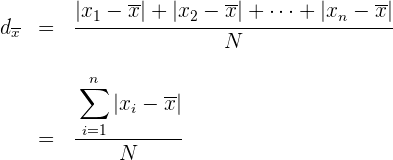
Beispiel: Berechne die mittlere Abweichung der Verteilung:

Wir berechnen zunächst den Mittelwert

Wir berechnen die mittlere absolute Abweichung
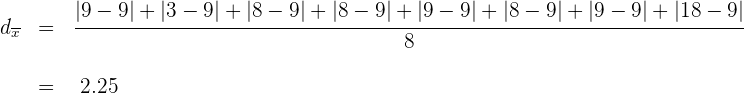
Mittlere absolute Abweichung für gruppierte Daten
Wenn die Daten in einer Häufigkeitstabelle gruppiert sind, lautet der Ausdruck für die mittlere Abweichung:
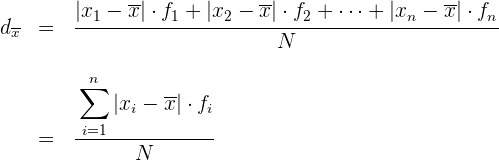
Beispiel: Berechne die mittlere absolute Abweichung der Verteilung:
 |  |  |  | 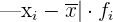 | |
|---|---|---|---|---|---|
 | 12,5 | 3 | 37,5 | 9,286 | 27,858 |
 | 17,5 | 5 | 87,5 | 4,286 | 21,43 |
 | 22,5 | 7 | 157,5 | 0,714 | 4,998 |
 | 27,5 | 4 | 110 | 5,714 | 22,856 |
 | 32,5 | 2 | 65 | 10,174 | 21,428 |
| 21 | 457,5 | 98,57 |
Wir führen die entsprechenden Operationen durch, um die Tabelle zu erhalten.
Wir addieren die letzten vier Spalten und berechnen den Mittelwert
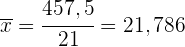
Die mittlere absolute Abweichung ist
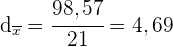
Varianz
Die Varianz ist das arithmetische Mittel des Quadrats der Abweichung vom Mittelwert einer statistischen Verteilung.
Die Varianz wird mit 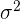 dargestellt.
dargestellt.
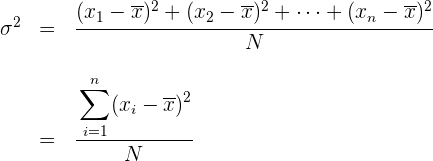
Varianz für gruppierte Daten

Um die Berechnung der Varianz zu vereinfachen, verwenden wir die folgenden Ausdrücke, die den vorherigen Ausdrücken gleichwertig sind.
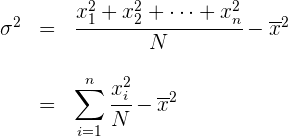
Beispiel: Berechne die Varianz der Verteilung:

Wir berechnen zunächst den Mittelwert

Mit dem Mittelwert können wir nun die Varianz berechnen

Beispiel: Berechne die Varianz der Verteilung in der Tabelle:
 |  |  |  | |
|---|---|---|---|---|
 | 15 | 1 | 15 | 225 |
 | 25 | 8 | 200 | 5000 |
 | 35 | 10 | 350 | 12 250 |
 | 45 | 9 | 405 | 18 225 |
 | 55 | 8 | 440 | 24 200 |
 | 65 | 4 | 260 | 16 900 |
 | 75 | 2 | 150 | 11 250 |
| 42 | 1 820 | 88 050 |
Wir führen die entsprechenden Operationen durch, um die Tabelle zu erhalten.
Wir addieren die letzten drei Spalten und berechnen den Mittelwert.
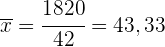
Die Varianz ist
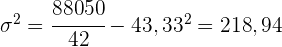
Standardabweichung
Die Standardabweichung ist die Quadratwurzel der Varianz.
Die Standardabweichung wird mit  dargestellt.
dargestellt.
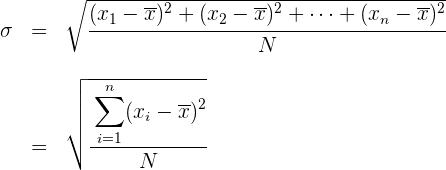
Standardabweichung für gruppierte Daten
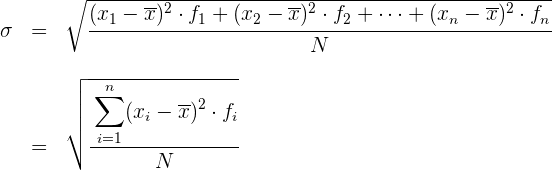
Um die Berechnung zu vereinfachen, verwenden wir die folgenden Ausdrücke, die den vorhergehenden gleichwertig sind.

Standardabweichung für gruppierte Daten

Variationskoeffizient
Der Variationskoeffizient ist das Verhältnis der Standardabweichung einer Stichprobe zu ihrem Mittelwert.
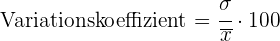
Standardwerte
Die Standardwerte ergeben sich aus der Division der Differenzwerte durch die Standardabweichung. Dieser Vorgang wird als Typisierung bezeichnet.
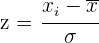
Mit KI zusammenfassen:












