Bestimme, ob es sich um qualitative oder quantitative Variablen handelt
Hier ein paar Beispiele für quantitative und qualitative Variablen:
- Dein Lieblingsessen.
- Ein Beruf, der dir gefällt.
- Die Anzahl der Tore, die dein Lieblings-Fußballclub in der letzten Saison geschossen hat.
- Die Anzahl der Schüler in deiner Schule.
- Die Augenfarbe deines Schulfreundes.
- Der IQ der Schüler in deiner Klasse.
Zeige an, wo es sich um qualitative und wo um quantitative Variablen handelt:
- Dein Lieblingsessen: Qualitativ
- Ein Beruf, der dir gefällt. Qualitativ
- Die Anzahl der Tore, die dein Lieblings-Fußballclub in der letzten Saison geschossen hat. Quantitativ
- Die Anzahl der Schüler in deiner Schule. Quantitativ
- Die Augenfarbe deines Schulfreundes. Qualitativ
- Der IQ der Schüler in deiner Klasse. Quantitativ
Zeige an, ob es sich bei den folgenden Variablen um diskrete oder stetige Variablen handelt
- Anzahl der Aktien, die täglich an der Börse verkauft werden.
- Temperaturen, die an einer Beobachtungsstelle stündlich aufgezeichnet werden.
- Laufzeit eines Fahrzeugs.
- Durchmesser der Räder verschiedener Autos.
- 5 Anzahl der Kinder von
 Familien.
Familien. - Jährliche Volkszählung in Deutschland.
Zeige an, ob es sich bei den folgenden Variablen um diskrete oder stetige Variablen handelt.
- Anzahl der Aktien, die täglich an der Börse verkauft werden. Diskret
- Temperaturen, die an einer Beobachtungsstelle stündlich aufgezeichnet werden. Stetig
- Laufzeit eines Fahrzeugs. Stetig
- Durchmesser der Räder verschiedener Autos. Stetig
- Anzahl der Kinder von
 Familien. Diskret
Familien. Diskret - Jährliche Volkszählung in Deutschland. Diskret
Bestimme die Art der folgenden Variablen (qualitativ bzw. quantitativ / diskret bzw. stetig)
- Die Nationalität einer Person.
- Die Zahl der Liter Wasser in einem Behälter.
- Die Zahl der Bücher in einem Bücherregal.
- Die Summe, die man beim Würfeln mit zwei Würfeln erhält.
- Der Beruf einer Person.
- Die Fläche unterschiedlicher Fließentypen in einem Gebäude.
Zeige an, ob es sich bei den folgenden Variablen um diskrete oder stetige Variablen handelt.
- Die Nationalität einer Person. Qualitativ
- Die Zahl der Liter Wasser in einem Behälter. Quantitativ und stetig
- Die Zahl der Bücher in einem Bücherregal. Quantitativ und diskret
- Die Summe, die man beim Würfeln mit zwei Würfeln erhält. Quantitativ und diskret
- Der Beruf einer Person. Qualitativ
- Die Fläche unterschiedlicher Fließentypen in einem Gebäude. Quantitativ und stetig
Erstellung von Häufigkeitstabellen: gemischte Übungen
Eine Testgruppe hat bei einer Untersuchung die folgenden Bewertungen erhalten:

Erstelle die zugehörige Tabelle mit der Häufigkeitsverteilung und zeichne das Häufigkeitspolygon ein.
Eine Testgruppe hat bei einer Untersuchung die folgenden Bewertungen erhalten:

Erstelle die zugehörige Tabelle mit der Häufigkeitsverteilung und zeichne das Häufigkeitspolygon ein.
 | Zählung |  |  |  |  |
|---|---|---|---|---|---|
 |  |  |  | 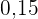 | 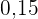 |
 |  |  |  | 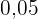 | 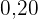 |
 |  |  |  |  | 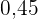 |
 |  |  |  | 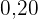 | 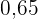 |
 |  |  |  | 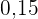 | 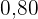 |
 |  |  |  | 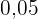 | 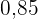 |
 | 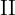 |  |  | 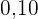 | 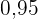 |
 |  |  |  | 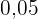 |  |
 |
In die zweite Zeile wird die Summe aus dem vorherigen Wert der kumulierten Häufigkeit und der entsprechenden absoluten Häufigkeit gebildet. So werden fortlaufend alle Zeilen bis zur letzten ausgefüllt, deren Wert  sein muss.
sein muss.
In die fünfte Zeile wird die relative Häufigkeit  eingetragen,
eingetragen,
die man erhält, indem man jede absolute Häufigkeit durch  teilt.
teilt.
In die sechste Spalte wird die kumulierte relative Häufigkeit  eingetragen.
eingetragen.
In die erste Zeile wird die erste relative Häufigkeit eingetragen.
In die zweite Zeile wird die Summe aus dem vorherigen Wert der kumulierten relativen Häufigkeit und der entsprechenden kumulierten relativen Häufigkeit gebildet. So werden fortlaufend alle Zeilen bis zur letzten ausgefüllt, deren Wert gleich  sein muss.
sein muss.
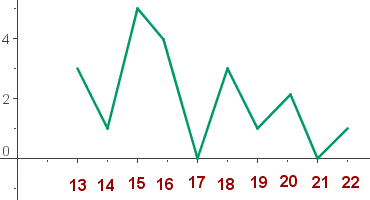
Das Häufigkeitspolygon
Trage auf der x-Achse die Daten und auf der y-Achse die absoluten Häufigkeiten ein.
Die folgende Zahlenreihe repräsentiert die Anzahl der Sterne der Hotels in einer Stadt:

Erstelle die zugehörige Tabelle mit der Häufigkeitsverteilung und stelle die Werte in einem Balkendiagramm grafisch dar.
Die folgende Zahlenreihe repräsentiert die Anzahl der Sterne der Hotels in einer Stadt:

Schritte zur Erstellung der Häufigkeitstabelle und grafischen Darstellung im Balkendiagramm.
 | Zählung |  |  |  |  |
|---|---|---|---|---|---|
 |  |  |  | 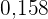 | 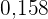 |
 |  |  |  | 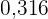 | 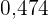 |
 |  |  |  | 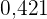 | 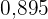 |
 |  |  |  | 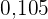 |  |
 |  |
In die vierte Spalte wird die kumulierte Häufigkeit  eingetragen.
eingetragen.
In die erste Zeile wird die erste absolute Häufigkeit eingetragen.
In die zweite Zeile wird die Summe aus dem vorherigen Wert der kumulierten Häufigkeit und der entsprechenden absoluten Häufigkeit gebildet. So werden fortlaufend alle Zeilen bis zur letzten ausgefüllt, deren Wert  sein muss.
sein muss.
In die fünfte Zeile wird die relative Häufigkeit  eingetragen,
eingetragen,
die man erhält, indem man jede absolute Häufigkeit durch  teilt.
teilt.
In die sechste Spalte wird die kumulierte relative Häufigkeit  eingetragen.
eingetragen.
In die erste Zeile wird die erste relative Häufigkeit eingetragen.
In die zweite Zeile wird die Summe aus dem vorherigen Wert der kumulierten relativen Häufigkeit und der entsprechenden kumulierten relativen Häufigkeit gebildet. So werden fortlaufend alle Zeilen bis zur letzten ausgefüllt, deren Wert gleich  sein muss.
sein muss.
Das Balkendiagramm
Trage auf der x-Achse die Daten und auf der y-Achse die absoluten Häufigkeiten ein.
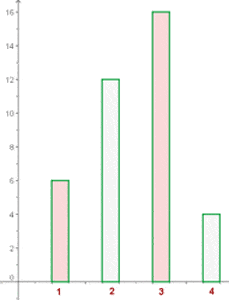
 Schüler haben die folgenden Noten in einer Prüfung erhalten:
Schüler haben die folgenden Noten in einer Prüfung erhalten:

Erstelle die zugehörige Tabelle mit der Häufigkeitsverteilung und stelle die Werte in einem Balkendiagramm grafisch dar.
 Schüler haben die folgenden Noten in einer Prüfung erhalten:
Schüler haben die folgenden Noten in einer Prüfung erhalten:

Schritte zur Erstellung der Häufigkeitstabelle und grafischen Darstellung im Balkendiagramm.
 |  |  |  |  |
|---|---|---|---|---|
 |  |  |  |  |
 1 1 |  |  |  | 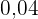 |
 |  |  | 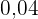 | 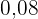 |
 |  |  | 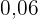 | 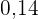 |
 |  |  | 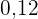 | 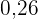 |
 |  |  | 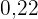 | 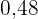 |
 |  |  | 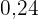 | 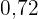 |
 |  |  | 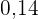 |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |  |  |  |
 |  |
In die vierte Spalte wird die kumulierte Häufigkeit  eingetragen.
eingetragen.
In die erste Zeile wird die erste absolute Häufigkeit eingetragen.
In die zweite Zeile wird die Summe aus dem vorherigen Wert der kumulierten Häufigkeit und der entsprechenden absoluten Häufigkeit gebildet. So werden fortlaufend alle Zeilen bis zur letzten ausgefüllt, deren Wert  sein muss.
sein muss.
In die fünfte Zeile wird die relative Häufigkeit ( ) eingetragen, die man erhält, indem man jede absolute Häufigkeit duch
) eingetragen, die man erhält, indem man jede absolute Häufigkeit duch  teilt.
teilt.
In die sechste Spalte wird die kumulierte relative Häufigkeit  eingetragen.
eingetragen.
In die erste Zeile wird die erste relative Häufigkeit eingetragen.
In die zweite Zeile wird die Summe aus dem vorherigen Wert der kumulierten relativen Häufigkeit und der entsprechenden kumulierten relativen Häufigkeit gebildet. So werden fortlaufend alle Zeilen bis zur letzten ausgefüllt, deren Wert gleich  sein muss.
sein muss.
Das Balkendiagramm
Trage auf der x-Achse die Daten und auf der y-Achse die absoluten Häufigkeiten ein.
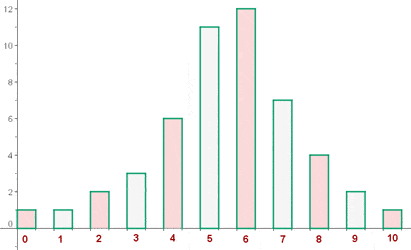
Die  Schüler einer Klasse haben die folgende Punktzahl von
Schüler einer Klasse haben die folgende Punktzahl von  möglichen Punkten in einer Physikklausur erhalten.
möglichen Punkten in einer Physikklausur erhalten.

- Erstelle die Häufigkeitstabelle.
- Erstelle das Histogramm und das Häufigkeitspolygon.
Die  Schüler einer Klasse haben die folgende Punktzahl von
Schüler einer Klasse haben die folgende Punktzahl von  möglichen Punkten in einer Physikklausur erhalten.
möglichen Punkten in einer Physikklausur erhalten.

a. Erstelle die Häufigkeitstabelle.
 |  |  |  |  | |
|---|---|---|---|---|---|
 |  |  |  |  | 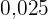 |
 | 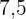 |  |  | 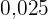 | 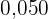 |
 | 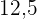 |  |  | 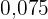 | 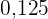 |
 | 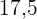 |  |  | 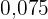 | 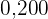 |
 | 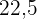 |  |  | 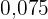 | 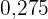 |
 | 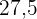 |  |  | 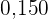 | 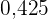 |
 | 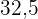 |  |  | 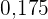 | 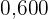 |
 | 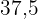 |  |  | 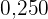 | 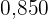 |
 | 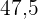 |  |  | 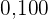 | 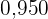 |
 | 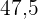 |  |  | 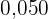 |  |
 |  |
In die vierte Spalte wird die kumulierte Häufigkeit  eingetragen.
eingetragen.
In die erste Zeile wird die erste absolute Häufigkeit eingetragen.
In die zweite Zeile wird die Summe aus dem vorherigen Wert der kumulierten Häufigkeit und der entsprechenden absoluten Häufigkeit gebildet. So werden fortlaufend alle Zeilen bis zur letzten ausgefüllt, deren Wert  sein muss.
sein muss.
In die fünfte Zeile wird die relative Häufigkeit ( ) eingetragen, die man erhält, indem man jede absolute Häufigkeit duch
) eingetragen, die man erhält, indem man jede absolute Häufigkeit duch  teilt.
teilt.
In die sechste Spalte wird die kumulierte relative Häufigkeit  eingetragen.
eingetragen.
In die erste Zeile wird die erste relative Häufigkeit eingetragen.
In die zweite Zeile wird die Summe aus dem vorherigen Wert der kumulierten relativen Häufigkeit und der entsprechenden kumulierten relativen Häufigkeit gebildet. So werden fortlaufend alle Zeilen bis zur letzten ausgefüllt, deren Wert gleich  sein muss.
sein muss.
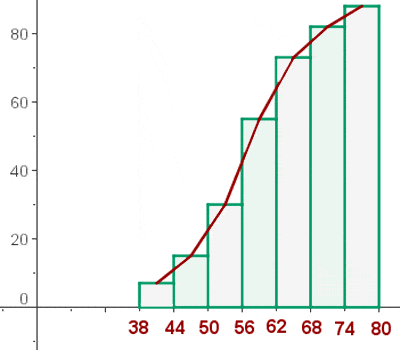
b. Erstelle das Histogramm und das Häufigkeitspolygon.
Das Histogramm
Das Häufigkeitspolygon wird gebildet, indem man die Mittelpunkte jedes Rechtecks miteinander verbindet
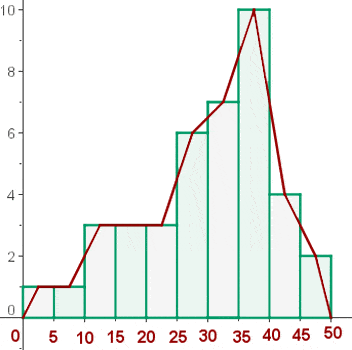
Für diese Aufgabe ist die folgende Häufigkeitsverteilung gegeben:
 |  |
|---|---|
 |  |
 |  |
 |  |
 |  |
 |  |
Berechne:
a. Den Modus, Median und Mittelwert.
b. Die Spannweite, mittlere Abweichung, Varianz und Standardabweichung.
Für diese Aufgabe ist die folgende Häufigkeitsverteilung gegeben:
 |  |
|---|---|
 |  |
 |  |
 |  |
 |  |
 |  |
Berechne:
a. Den Modus, Median und Mittelwert.
b. Die Spannweite, mittlere Abweichung, Varianz und Standardabweichung.
Ergänze die Tabelle mit folgenden Maßen:
der kumulierten Häufigkeit ( ), um den Median zu berechnen
), um den Median zu berechnen
dem Produkt aus der Variablen und ihrer absoluten Häufigkeit ( ), um den Mittelwert zu berechnen
), um den Mittelwert zu berechnen
der Abweichung bezüglich des Mittelwerts und ihrem Produkt mit der absoluten Häufigkeit
und ihrem Produkt mit der absoluten Häufigkeit  , um die mittlere Abweichung zu berechnen
, um die mittlere Abweichung zu berechnen
dem Produkt aus der Variablen zum Quadrat und ihrer absoluten Häufigkeit (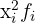 ), um die Varianz und die Standardabweichung zu berechnen
), um die Varianz und die Standardabweichung zu berechnen
 |  |  |  |  |  | 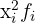 |
|---|---|---|---|---|---|---|
 |  |  |  | 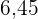 | 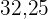 |  |
 |  |  |  | 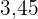 | 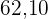 | 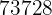 |
 |  |  |  | 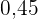 | 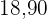 |  |
 |  |  |  | 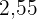 | 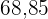 |  |
 |  |  |  | 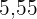 | 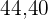 |  |
 |  |  |  |
Modus
Der Modus ist der Wert mit der höchsten absoluten Häufigkeit.
In der Spalte der  entspricht die absolute Häufigkeit
entspricht die absolute Häufigkeit  dem Wert
dem Wert  .
.
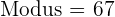 .
.
Median
Um den Median zu berechnen, teilt man  durch
durch  . Man kann feststellen, dass sich in der Zeile der
. Man kann feststellen, dass sich in der Zeile der  der Wert für
der Wert für  befindet, der am nächsten an
befindet, der am nächsten an  liegt, und zwar der Wert
liegt, und zwar der Wert  , der dem Median
, der dem Median  entspricht.
entspricht.
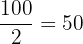
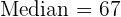
Mittelwert
Berechne die Summe der Variablen und ihrer absoluten Häufigkeit ( ), die
), die  ist, und teile sie durch
ist, und teile sie durch  .
.
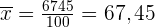
Mittlere Abweichung
Berechne die Summe der Produkte der Abweichungen vom Mittelwert mit ihren zugehörigen absoluten Häufigkeiten  , die
, die 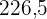 ist, und teile durch
ist, und teile durch  .
.
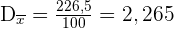
Spannweite
Berechne die Differenz aus dem größten und kleinsten Wert.
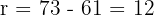 .
.
Varianz
Berechne die Summe aus  , teile sie durch
, teile sie durch  und ziehe vom Ergebnis den Mittelwert zum Quadrat
und ziehe vom Ergebnis den Mittelwert zum Quadrat 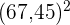 ab.
ab.
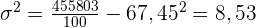 .
.
Standardabweichung
Bilde die Quadratwurzel der Varianz
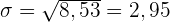
Berechne Mittelwert, Median und Modus der folgenden Zahlenreihe:

Berechne Mittelwert, Median und Modus der folgenden Zahlenreihe:

Erstelle eine Tabelle mit den folgenden Spalten:
Werte der Variablen ( ).
).
Absolute Häufigkeiten ( ).
).
Kumulierte Häufigkeiten ( ), um den Median zu berechnen.
), um den Median zu berechnen.
Produkt aus der Variablen und ihrer absoluten Häufigkeit ( ), um den Mittelwert zu berechnen.
), um den Mittelwert zu berechnen.
 |  |  |  |
|---|---|---|---|
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |
Modus
Der Modus ist der Wert mit der höchsten absoluten Häufigkeit.
In der Spalte der  entspricht die absolute Häufigkeit
entspricht die absolute Häufigkeit  dem Wert
dem Wert  .
.
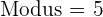 .
.
Median
Um den Median zu berechnen, teilt man  durch
durch  . Man kann feststellen, dass sich in der Zeile der
. Man kann feststellen, dass sich in der Zeile der  der Wert
der Wert  befindet, der
befindet, der  entspricht.
entspricht.
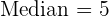 .
.
Mittelwert
Berechne die Summe der Variablen und ihrer absoluten Häufigkeit ( ), die
), die  ist und teile durch
ist und teile durch  .
.
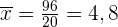 .
.
Ermittle die Varianz und die Standardabweichung der folgenden Datenreihe:

Ermittle die Varianz und die Standardabweichung der folgenden Datenreihe:

Berechne den Mittelwert:
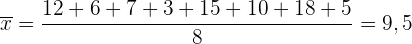 .
.
Wende die Varianzformel an:
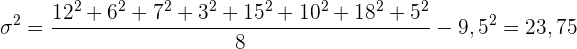 .
.
Ziehe die Quadratwurzel der Varianz:
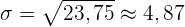 .
.
Berechne Mittelwert, Median und Modus der folgenden Zahlenreihe:

Berechne Mittelwert, Median und Modus der folgenden Zahlenreihe:

Modus
Der Modus ist  , da sich dieser Wert am häufigsten wiederholt.
, da sich dieser Wert am häufigsten wiederholt.
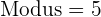 .
.
Median
Da die Reihe eine gerade Anzahl von Werten hat, ist der Median der Mittelwert zwischen den beiden mittleren Werten.
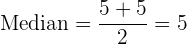 .
.
Mittelwert
Wende die Formel für den Mittelwert an.
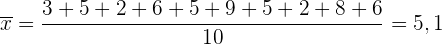 .
.
Ermittle die Varianz, die mittlere Abweichung und die Standardabweichung der folgenden Zahlenreihe:
Ermittle die Varianz, die mittlere Abweichung und die Standardabweichung der folgenden Zahlenreihe:
a. 
Mittelwert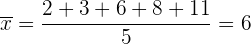
Mittlere Abweichung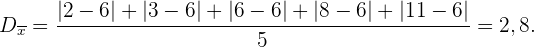
Varianz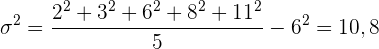 .
.
Standardabweichung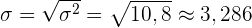 .
.
b. 
Mittelwert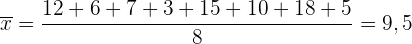 .
.
Mittlere Abweichung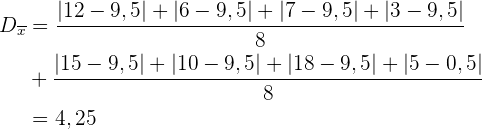 .
.
Varianz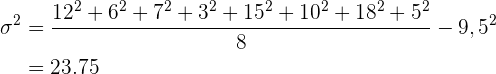
Standardabweichung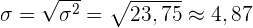 .
.
Aus einem Test mit Angestellten einer Fabrik gingen folgende Ergebnisse hervor:
 | |
|---|---|
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Erstelle das Histogramm und das Polygon der kumulierten Häufigkeiten.
Aus einem Test mit Angestellten einer Fabrik gingen folgende Ergebnisse hervor:
 | |
|---|---|
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Erstelle das Histogramm und das Polygon der kumulierten Häufigkeiten.
Füge eine neue Spalte hinzu, in welche du die kumulierte Häufigkeit ( ) einträgst:
) einträgst:
In die erste Zeile wird die erste absolute Häufigkeit eingetragen.
In die zweite Zeile wird die Summe aus dem vorherigen Wert der kumulierten Häufigkeit und der entsprechenden absoluten Häufigkeit gebildet. So werden fortlaufend alle Zeilen bis zur letzten ausgefüllt, deren Wert  sein muss.
sein muss.
 |  | |
|---|---|---|
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |
Gegeben seien die folgenden statistischen Zahlenreihen:
a. 
b. 
Berechne
Modus, Median und Mittelwert
Mittlere Abweichung, Varianz und Standardabweichung
Die Quartile  und
und  .
.
Die Dezile  und
und  .
.
Die Perzentile  und
und  .
.
Gegeben seien die folgenden statistischen Zahlenreihen:
a. 
b. 
Berechne
Modus, Median und Mittelwert
Mittlere Abweichung, Varianz und Standardabweichung
Die Quartile  und
und  .
.
Die Dezile  und
und  .
.
Die Perzentile  und
und  .
.
a. 
Modus
Es gibt keinen Modus, da alle Werte dieselbe Häufigkeit haben.
Median
Ordne die Daten der Reihenfolge nach aufsteigend:

Der Median ist daher
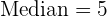 .
.
Mittelwert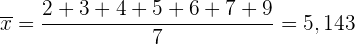
Varianz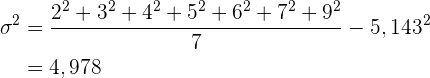
Standardabweichung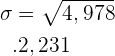
Mittlere Abweichung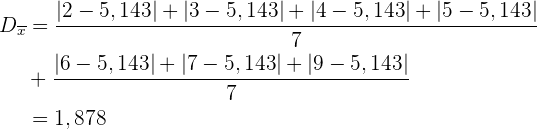
Spannweite
Quartile
Dezile
Die Formel zur Bestimmung der Dezile lautet

Die gesuchten Dezile befinden sich daher an den Stellen:
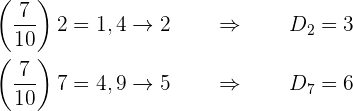
Perzentile
Die Formel zur Bestimmung der Perzentile lautet

Die gesuchten Perzentile befinden sich daher an den Stellen:
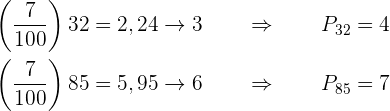
b. 
Modus
Es gibt keinen Modus, da alle Werte dieselbe Häufigkeit haben.
Median
Ordne die Daten der Reihenfolge nach aufsteigend:

Der Median ist daher
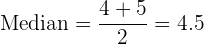 .
.
Mittelwert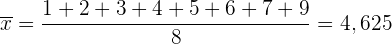
Varianz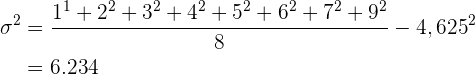
Standardabweichung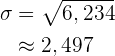
Mittlere Abweichung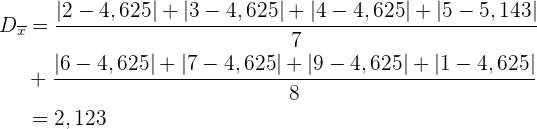
Spannweite
Quartile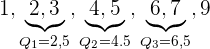
Dezile
Die Formel zur Bestimmung der Dezile lautet

Die gesuchten Dezile befinden sich daher an den Stellen:
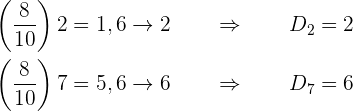
Perzentile
Die Formel zur Bestimmung der Perzentile lautet

Die gesuchten Perzentile befinden sich daher an den Stellen:
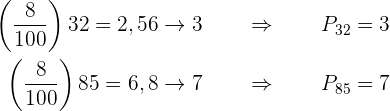
Gegeben sei die folgende statistische Zahlenreihe:
 | |
|---|---|
 |  |
 |  |
 |  |
 |  |
 |  |
Ermittle:
a)) Den Modus, Median und Mittelwert.
b)) Die Spannweite, mittlere Abweichung und Varianz.
c)) Die Quartile  und
und  .
.
d)) Die Dezile  und
und  .
.
e) Die Perzentile  und
und  .
.
Ergänze die Tabelle mit:
der kumulierten Häufigkeit ( ), um den Median zu berechnen.
), um den Median zu berechnen.
dem Produkt aus der Variablen und ihrer absoluten Häufigkeit ( ), um den Mittelwert zu berechnen.
), um den Mittelwert zu berechnen.
der Abweichung bezüglich des Mittelwerts  und ihrem Produkt mit der absoluten Häufigkeit
und ihrem Produkt mit der absoluten Häufigkeit  , um die mittlere Abweichung zu berechnen
, um die mittlere Abweichung zu berechnen
dem Produkt aus der Variablen zum Quadrat und ihrer absoluten Häufigkeit (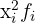 ), um die Varianz und die Standardabweichung zu berechnen
), um die Varianz und die Standardabweichung zu berechnen
 |  |  |  |  | 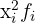 | |
|---|---|---|---|---|---|---|
 | 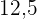 |  |  | 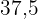 | 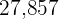 | 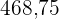 |
 | 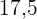 |  |  | 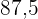 | 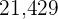 | 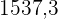 |
 | 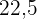 |  |  | 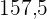 |  | 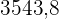 |
 | 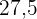 |  |  |  | 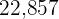 |  |
 | 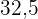 |  |  |  | 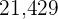 | 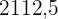 |
 | 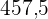 | 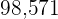 | 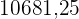 |
Modus
Suche zuerst das Intervall, indem sich der Modus befindet. Dieses ist das Intervall mit der höchsten absoluten Häufigkeit ( )
)
Die Modalklasse lautet: 
Wende die Formel zur Berechnung des Modus für gruppierte Daten an, indem du folgende Daten extrahierst:
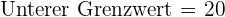 .
.
 .
.
 .
.


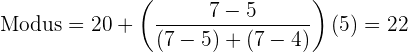
Median
Suche das Intervall, in dem sich der Median befindet. Teile hierzu  durch
durch  , da der Median der mittlere Wert ist
, da der Median der mittlere Wert ist
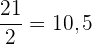 .
.
Ermittle in der Spalte der kumulierten Häufigkeit ( ) das Intervall, das den Wert
) das Intervall, das den Wert 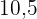 enthält
enthält
Die Klasse des Medians lautet:  .
.
Wende die Formel zur Berechnung des Medians für gruppierte Daten an, indem du folgende Daten extrahierst:
 .
.
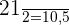 .
.
 .
.
 .
.
 .
.
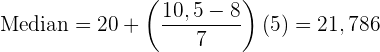 .
.
Mittelwert
Berechne die Summe der Variablen und ihrer absoluten Häufigkeit ( ), die
), die 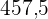 ist und teile sie durch
ist und teile sie durch 
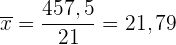
Mittlere Abweichung
Berechne die Summe der Produkte der Abweichungen vom Mittelwert mit ihren zugehörigen absoluten Häufigkeiten  , die
, die 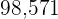 ist, und teile durch
ist, und teile durch 
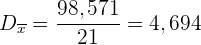
Varianz
Berechne die Summe aus 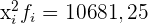 , teile sie durch
, teile sie durch  und ziehe vom Ergebnis den Mittelwert zum Quadrat,
und ziehe vom Ergebnis den Mittelwert zum Quadrat, 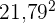 , ab.
, ab.
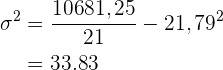
Standardabweichung
Bilde die Quadratwurzel der Varianz
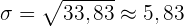
Quartile
Berechne das erste Quartil
Suche das Intervall, in dem sich das erste Quartil befindet, indem du  mal
mal  multiplizierst und das Ergebnis durch
multiplizierst und das Ergebnis durch  teilst
teilst
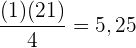
Suche in der Spalte der kumulierten Häufigkeit ( ) das Intervall, das
) das Intervall, das 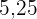 enthält
enthält
Die Modalklasse von  lautet:
lautet: 
Wende die Formel zur Berechnung der Quartile für gruppierte Daten an, indem du folgende Daten extrahierst:




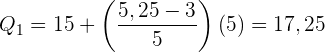
Ermittle das dritte Quartil
Suche das Intervall, in dem sich das dritte Quartil befindet, indem du  mal
mal  multiplizierst und das Ergebnis durch
multiplizierst und das Ergebnis durch  teilst
teilst
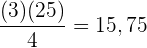
Suche in der Spalte der kumulierten Häufigkeit ( ) das Intervall, das
) das Intervall, das 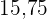 enthält
enthält
Die Modalklasse von  ist:
ist: 
Wende die Formel zur Berechnung der Quartile für gruppierte Daten an, indem du folgende Daten extrahierst:




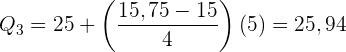
Dezile
Ermittle das dritte Dezil
Suche das Intervall, indem sich das dritte Dezil befindet, indem du  mit
mit  multiplizierst und das Ergebnis durch
multiplizierst und das Ergebnis durch  teilst
teilst
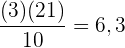
Suche in der Spalte der kumulierten Häufigkeit ( ) das Intervall, das
) das Intervall, das 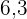 enthält
enthält
Die Modalklasse von  ist:
ist: 
Wende die Formel zur Berechnung der Dezile für gruppierte Daten an, indem du folgende Daten extrahierst:




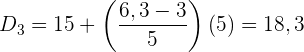
Berechne das sechste Dezil
Suche das Intervall, indem sich das sechste Dezil befindet, indem du  mit
mit  multiplizierst und das Ergebnis durch
multiplizierst und das Ergebnis durch  teilst
teilst
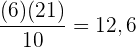
Suche in der Spalte der kumulierten Häufigkeit ( ) das Intervall, das
) das Intervall, das 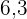 enthält
enthält
Die Modalklasse von  ist:
ist: 
Wende die Formel zur Berechnung der Dezile für gruppierte Daten an, indem du folgende Daten extrahierst:




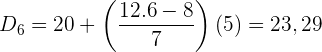
Perzentile
Das Perzentil  ist gleich dem Dezil
ist gleich dem Dezil 
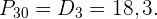
Berechne das Perzentil 70
Suche das Intervall, in dem sich das Perzentil  befindet, indem du
befindet, indem du  mit
mit  multiplizierst und das Ergebnis durch
multiplizierst und das Ergebnis durch  teilst
teilst
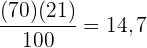
Suche in der Spalte der kumulierten Häufigkeit ( ) das Intervall, das
) das Intervall, das 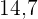 enthält
enthält
Die Modalklasse von  ist:
ist: 
Wende die Formel zur Berechnung der Perzentile für gruppierte Daten an, indem du folgende Daten extrahierst:




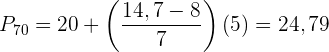
Gegeben sei die folgende statistische Zahlenreihe:
 | |
|---|---|
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Ermittle:
a. Den Median und den Modus.
b. Die Quartile  und
und  .
.
c. Den Mittelwert.
Füge eine neue Spalte hinzu, in welche du die kumulierte Häufigkeit ( ) einträgst:
) einträgst:
In die erste Zeile wird die erste absolute Häufigkeit eingetragen.
In die zweite Zeile wird die Summe aus dem vorherigen Wert der kumulierten Häufigkeit und der entsprechenden absoluten Häufigkeit gebildet. So werden fortlaufend alle Zeilen bis zur letzten ausgefüllt, deren Wert  sein muss.
sein muss.
 |  |  | |
|---|---|---|---|
 | 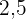 |  |  |
 | 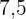 |  |  |
 | 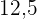 |  |  |
 | 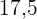 |  |  |
 | 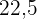 |  |  |
 |  |  | |
 |
Modus
Suche zuerst das Intervall, indem sich der Modus befindet. Dieses ist das Intervall mit der höchsten absoluten Häufigkeit ( )
)
Die Modalklasse lautet: 
Wende die Formel zur Berechnung des Modus für gruppierte Daten an, indem du folgende Daten extrahierst:
Unterer Grenzwert: 




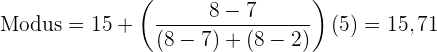
Median
Suche das Intervall, in dem sich der Median befindet. Teile hierzu  durch
durch  , da der Median der mittlere Wert ist
, da der Median der mittlere Wert ist
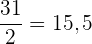
Suche in der Spalte der kumulierten Häufigkeit ( ) das Intervall, das
) das Intervall, das 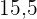 enthält
enthält
Die Klasse des Medians lautet: 
Wende die Formel zur Berechnung des Medians für gruppierte Daten an, indem du folgende Daten extrahierst:




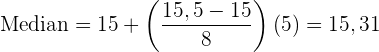
Quartile
Berechne das erste Quartil
Suche das Intervall, in dem sich das erste Quartil befindet, indem du mit
mit  multiplizierst und das Ergebnis durch
multiplizierst und das Ergebnis durch  teilst
teilst
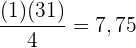
Suche in der Spalte der kumulierten Häufigkeit ( ) das Intervall, das
) das Intervall, das 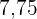 enthält
enthält
Die Klasse von  ist:
ist: 
Wende die Formel zur Berechnung der Quartile für gruppierte Daten an, indem du folgende Daten extrahierst:




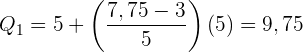
Ermittle das dritte Quartil
Suche das Intervall, in dem sich das dritte Quartil befindet, indem du  mit
mit  multiplizierst und das Ergebnis durch
multiplizierst und das Ergebnis durch  teilst
teilst
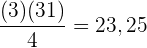
Suche in der Spalte der kumulierten Häufigkeit  ) das Intervall, das
) das Intervall, das 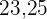 enthält
enthält
Die Klasse von  ist:
ist: 
Wende die Formel zur Berechnung der Quartile für gruppierte Daten an, indem du folgende Daten extrahierst:




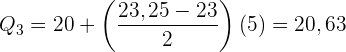
Mittelwert
Der Mittelwert kann nicht berechnet werden, da die Grenze der Klasse des letzten Intervalls nicht ermittelt werden kann.
Mit KI zusammenfassen:



