1 Die Höchsttemperaturen in einer Stadt im Juni waren: 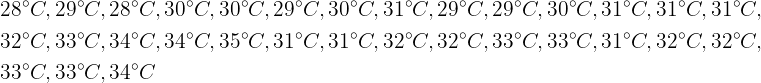
Berechne den Modus:
D =
Dieses Feld ist erforderlich.
Bererchne den Median:
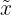 =
=
Dieses Feld ist erforderlich.
Berechne den Mittelwert:
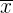 =
=
Dieses Feld ist erforderlich.
Berechne den Rang:
R =
Dieses Feld ist erforderlich.
Berechne die mittlere absolute Abweichung:
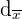 =
=
Dieses Feld ist erforderlich.
Berechne die Varianz:
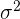 =
=
Dieses Feld ist erforderlich.
Berechne die Standardabweichung:
 =
=
Dieses Feld ist erforderlich.
| xi | fi | xi · fi | |x − x| | |x − x| · fi | xi² · fi |
|---|---|---|---|---|---|
| 28 | 2 | 56 | 3.32 | 6.64 | 1 568 |
| 29 | 4 | 116 | 2.32 | 9.28 | 3 364 |
| 30 | 4 | 120 | 1.32 | 5.28 | 3 600 |
| 31 | 7 | 217 | 0.32 | 2.24 | 6 727 |
| 32 | 5 | 160 | 0.68 | 3.4 | 5 120 |
| 33 | 5 | 165 | 1.68 | 8.4 | 5 445 |
| 34 | 3 | 102 | 2.68 | 8.04 | 3 468 |
| 35 | 1 | 35 | 3.68 | 3.68 | 1 225 |
| 31 | 971 | 46.96 | 30 517 |
Modus Wir denken daran, dass der Modus der Wert ist, der die größte absolute Häufigkeit hat. Das heißt, der Wert, der am häufigsten vorkommt. In diesem Fall ist der Modus 31, da diese die Temperatur ist, die im Juni am häufigsten erreicht wurde.
Median Wir denken daran, dass der Median der Wert ist, der die zentrale Stelle aller Daten einnimmt, wenn diese aufsteigend angeordnet sind. Wenn die Reihe eine ungerade Anzahl von Messwerten hat, ist der Median der mittlere Wert der Reihe, und wenn die Reihe eine gerade Anzahl von Werten hat, ist der Median der Mittelwert zwischen den beiden mittleren Werten. Zunächst dividieren wir 31/2 und erhalten 15,5. Das heißt, wenn wir die Temperaturen in eine Reihenfolge bringen, wäre der Median der Wert an Stelle 16. 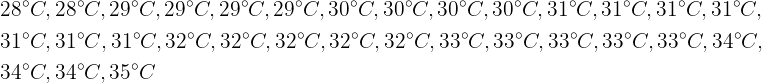 Und somit
Und somit 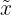 = 31
= 31
Mittelwert Das arithmetische Mittel ist der Wert, der sich aus der Summe aller Daten und der Division des Ergebnisses durch die Gesamtzahl der Daten ergibt und wird mit 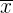 angegeben. Das heißt,
angegeben. Das heißt, 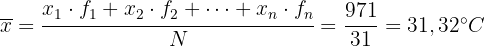
Rang Der Rang ist die Differenz zwischen dem größten und dem kleinsten Wert einer statistischen Verteilung. Somit gilt 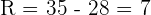
Mittlere absolute Abweichung Die Abweichung vom Mittelwert ist die Differenz zwischen jedem Wert der statistischen Variablen und dem arithmetischen Mittel. 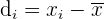 Die mittlere absolute Abweichung ist das arithmetische Mittel der Beträge der Abweichungen vom Mittelwert. Die mittlere absolute Abweichung wird mit
Die mittlere absolute Abweichung ist das arithmetische Mittel der Beträge der Abweichungen vom Mittelwert. Die mittlere absolute Abweichung wird mit 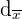 angegeben.
angegeben. 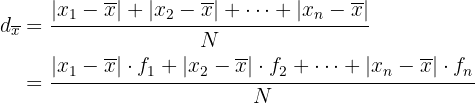 somit
somit 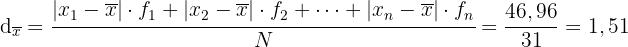
Varianz Die Varianz ist das arithmetische Mittel der Quadrate der Abweichungen vom Mittelwert einer statistischen Verteilung. Die Varianz wird mit 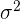 angegeben.
angegeben. 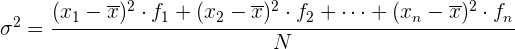 äquivalent zu
äquivalent zu 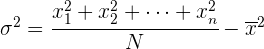 Und somit gilt
Und somit gilt 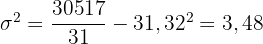
Standardabweichung Die Standardabweichung ist die Quadratwurzel der Varianz, weshalb
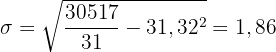
2Eine statistische Verteilung ist durch die folgende Tabelle gegeben:
 |  |
|---|---|
 |  |
 |  |
 |  |
 |  |
 |  |
Berechne:
Modus:
D =
Dieses Feld ist erforderlich.
Median:
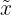 =
=
Dieses Feld ist erforderlich.
Mittelwert:
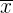 =
=
Dieses Feld ist erforderlich.
Rang:
R =
Dieses Feld ist erforderlich.
Berechne die mittlere absolute Abweichung:
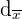 =
=
Dieses Feld ist erforderlich.
Berechne die Varianz:
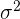 =
=
Dieses Feld ist erforderlich.
Berechne die Standardabweichung:
 =
=
Dieses Feld ist erforderlich.
Wir vervollständigen die Tabelle mit:
- Der kumulierten Häufigkeit (
 ), um den Median zu berechnen
), um den Median zu berechnen
- Dem Produkt aus der Variablen und ihrer absoluten Häufigkeit (
 ) zur Berechnung des Mittelwerts
) zur Berechnung des Mittelwerts
- Der Abweichung vom Mittelwert
 und ihr Produkt mit der absoluten Häufigkeit
und ihr Produkt mit der absoluten Häufigkeit  zur Berechnung der mittleren absoluten Abweichung
zur Berechnung der mittleren absoluten Abweichung
- Dem Produkt aus der quadrierten Variablen und ihrer absoluten Häufigkeit (
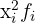 ) zur Berechnung der Varianz und der Standardabweichung
) zur Berechnung der Varianz und der Standardabweichung
 |  |  |  | 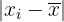 | 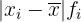 | 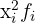 |
|---|---|---|---|---|---|---|
 |  |  |  |  |  |  |
 |  |  |  |  |  | 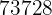 |
 |  |  |  | 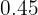 |  |  |
 |  |  |  |  |  |  |
 |  |  |  |  |  |  |
 |  |  |  |
Modus
Der Modus ist der Wert mit der höchsten absoluten Häufigkeit.
Wir schauen in die Spalte  und die höchste absolute Häufigkeit,
und die höchste absolute Häufigkeit,  , entspricht
, entspricht  .
.
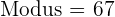 .
.
Median
Um den Median zu berechnen, dividieren wir  durch
durch  und sehen, dass bei den Werten von
und sehen, dass bei den Werten von  die
die  die Zahl ist, die der Zahl
die Zahl ist, die der Zahl  am nächsten kommt, und
am nächsten kommt, und  entspricht.
entspricht.
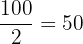
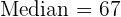
Mittelwert
Wir berechnen die Summe der Variablen anhand ihrer absoluten Häufigkeit ( ), die
), die  beträgt, und dividieren durch
beträgt, und dividieren durch  .
.
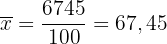
Mittlere absolute Abweichung
Wir berechnen die Summe der Produkte aus den Abweichungen vom Mittelwert und ihren entsprechenden absoluten Häufigkeiten  , was
, was 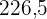 ergibt, und dividieren durch
ergibt, und dividieren durch  .
.
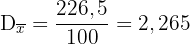
Rang
Wir berechnen die Differenz zwischen dem höchsten und dem niedrigsten Wert
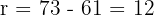 .
.
Varianz
Wir berechnen die Summe von  , dividieren sie durch
, dividieren sie durch  und subtrahieren vom Ergebnis das arithmetische Mittel zum Quadrat
und subtrahieren vom Ergebnis das arithmetische Mittel zum Quadrat 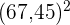
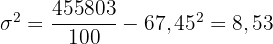 .
.
Standardabweichung
Und nun die Quadratwurzel der Varianz
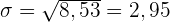
3 Berechne den Mittelwert, den Median und den Modus der folgenden Zahlenreihe:

Modus:
D =
Dieses Feld ist erforderlich.
Median:
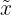 =
=
Dieses Feld ist erforderlich.
Mittelwert:
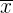 =
=
Dieses Feld ist erforderlich.
Modus
Der Modus ist  , da dies der Wert ist, der am häufigsten vorkommt.
, da dies der Wert ist, der am häufigsten vorkommt.
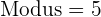 .
.
Median
Die Reihe hat eine gerade Anzahl von Werten, der Median ist der Mittelwert zwischen den beiden mittleren Werten.
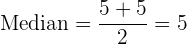 .
.
Mittelwert
Wir wenden die Formel für den Mittelwert an.
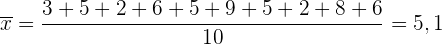 .
.
4 Berechne die mittlere absolute Abweichung, die Varianz und die Standardabweichung der folgenden Zahlenreihe:

Mittlere absolute Abweichung:
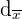 =
=
Dieses Feld ist erforderlich.
Varianz:
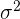 =
=
Dieses Feld ist erforderlich.
Standardabweichung:
 =
=
Dieses Feld ist erforderlich.
Mittelwert
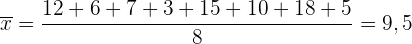 .
.
Mittlere absolute Abweichung
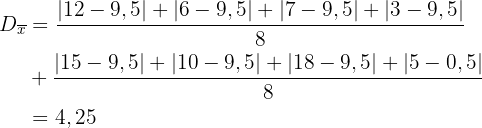 .
.
Varianz
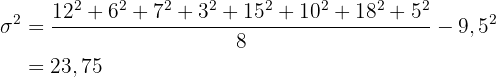
Standardabweichung
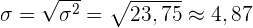 .
.
Mit KI zusammenfassen:


