Ermittle die mittlere Abweichung, Varianz und Standardabweichung der folgenden Zahlenreihe:
a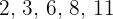 
.
b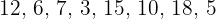 
.
a Für die Zahlenreihe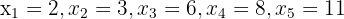 
mit 
nehmen wir folgende Berechnungen vor.
Zur Ermittlung der mittleren Abweichung muss der Mittelwert berechnet werden.
Mittelwert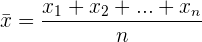
Berechne dann den Wert der mittleren Abweichung.
Mittlere Abweichung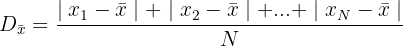
Berechne nun die Varianz.
Varianz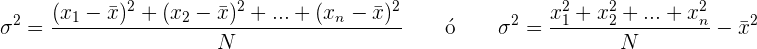
Abschließend kann die Standardabweichung berechnet werden.
Standardabweichung
b Für die Zahlenreihe 
con 
nehmen wir folgende Berechnungen vor.
Zur Ermittlung der mittleren Abweichung muss der Mittelwert berechnet werden.
Mittelwert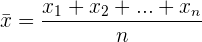
Berechne dann den Wert der mittleren Abweichung.
Mittlere Abweichung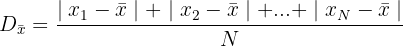
Berechne nun die Varianz.
Varianz
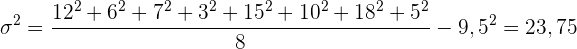
Abschließend kann die Standardabweichung berechnet werden.
Standardabweichung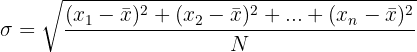
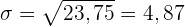
Ein Kinderarzt besitzt eine Tabelle mit Monatszahlen von 50 Kindern, die den Monat angeben, in dem sie zu Laufen begonnen haben. Berechne die Varianz.
| Monate | Kinder |
|---|---|
| 9 | 1 |
| 10 | 4 |
| 11 | 9 |
| 12 | 16 |
| 13 | 11 |
| 14 | 8 |
| 15 | 1 |
Ergänze die Tabelle mit:
1 Berechne das Produkt der Variable mal der absoluten Häufigkeit (xi · fi), um den Mittelwert zu berechnen.
2 Berechne das Produkt der Variable zum Quadrat mal der absoluten Häufigkeit (xi² · fi), um die Varianz und die Standardabweichung zu berechnen
| xi | fi | xi · fi | x²i · fi |
|---|---|---|---|
| 9 | 1 | 9 | 81 |
| 10 | 4 | 40 | 400 |
| 11 | 9 | 99 | 1089 |
| 12 | 16 | 192 | 2304 |
| 13 | 11 | 143 | 1859 |
| 14 | 8 | 112 | 1568 |
| 15 | 1 | 15 | 225 |
| 50 | 610 | 7526 |
Arithmetisches Mittel (Mittelwert)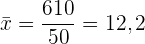
Varianz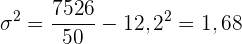
Die folgende Tabelle zeigt die Ergebnisse auf, die beim 120maligen Würfeln mit zwei Würfeln erzielt wurden. Berechne die Varianz.
| Würfelsummen | Häufigkeit |
|---|---|
| 2 | 3 |
| 3 | 8 |
| 4 | 9 |
| 5 | 11 |
| 6 | 20 |
| 7 | 19 |
| 8 | 16 |
| 9 | 13 |
| 10 | 11 |
| 11 | 6 |
| 12 | 4 |
Lösung:
Füge die Spalten xi · fi und xi² · fi hinzu
| xi | fi | xi · fi | xi² · fi |
|---|---|---|---|
| 2 | 3 | 6 | 12 |
| 3 | 8 | 24 | 72 |
| 4 | 9 | 36 | 144 |
| 5 | 11 | 55 | 275 |
| 6 | 20 | 120 | 720 |
| 7 | 19 | 133 | 931 |
| 8 | 16 | 128 | 1024 |
| 9 | 13 | 117 | 1053 |
| 10 | 11 | 110 | 1100 |
| 11 | 6 | 66 | 726 |
| 12 | 4 | 48 | 576 |
| 120 | 843 | 6633 |
Arithmetisches Mittel (Mittelwert)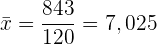
Varianz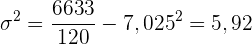
Berechne die Varianz der folgenden statistischen Verteilung.
| fi | |
|---|---|
| [10, 15) | 3 |
| [15, 20) | 5 |
| [20, 25) | 7 |
| [25, 30) | 4 |
| [30, 35) | 2 |
Varianz
Berechne die Varianz der folgenden statistischen Verteilung.
| xi | fi | xi · fi | xi² · fi | |
|---|---|---|---|---|
| [10, 20) | 15 | 1 | 15 | 225 |
| [20, 30) | 25 | 8 | 200 | 5000 |
| [30,40) | 35 | 10 | 350 | 12 250 |
| [40, 50) | 45 | 9 | 405 | 18 225 |
| [50, 60) | 55 | 8 | 440 | 24 200 |
| [60,70) | 65 | 4 | 260 | 16 900 |
| [70, 80) | 75 | 2 | 150 | 11 250 |
| 42 | 1 820 | 88 050 |
Mittelwert
Varianz
Die Körpergrößen der Spieler einer Basketballmannschaft sind in folgender Tabelle ersichtlich. Berechne die Varianz.
| Körpergröße | Anzahl der Spieler |
|---|---|
| [1,70, 1,75) | 1 |
| [1,75, 1,80) | 3 |
| [1,80, 1,85) | 4 |
| [1,85, 1,90) | 8 |
| [1,90, 1,95) | 5 |
| [1,95, 2,00) | 2 |
Ergänze die Tabelle um die Spalten xi · fi und xi² · fi
| xi | fi | Fi | xi · fi | xi² · fi | |
|---|---|---|---|---|---|
| [1,70, 1,75) | 1,725 | 1 | 1 | 1,725 | 2,976 |
| [1,75, 1,80) | 1,775 | 3 | 4 | 5,325 | 9,452 |
| [1,80, 1,85) | 1,825 | 4 | 8 | 7,3 | 13,323 |
| [1,85, 1,90) | 1,875 | 8 | 16 | 15 | 28,125 |
| [1,90, 1,95) | 1,925 | 5 | 21 | 9,625 | 18,53 |
| [1,95, 2,00) | 1,975 | 2 | 23 | 3,95 | 7,802 |
| 23 | 42,925 | 80,213 |
Mittelwert
Varianz
Gegeben sei die folgende statistische Verteilung. Berechne die Varianz.
| fi | |
|---|---|
| [0, 5) | 3 |
| [5, 10) | 5 |
| [10, 15) | 7 |
| [15, 20) | 8 |
| [20, 25) | 2 |
| [25, ∞) | 6 |
| xi | fi | Fi | |
|---|---|---|---|
| [0, 5) | 2,5 | 3 | 3 |
| [5, 10) | 7,5 | 5 | 8 |
| [10, 15) | 12,5 | 7 | 15 |
| [15, 20) | 17,5 | 8 | 23 |
| [20, 25) | 22,5 | 2 | 25 |
| [25, ∞) | 6 | 31 | |
| 31 |
Mittelwert
Der Mittelwert kann nicht berechnet werden, da die Grenze der Klasse des letzten Intervalls nicht ermittelt werden kann.
Varianz
Ohne Mittelwert ist es nicht möglich, die Varianz zu ermitteln.
Gegeben seien die folgenden Daten: 
.
1 Berechne ihren Mittelwert und ihre Varianz.
2 Wenn wir alle Daten mit 
multiplizieren, welchen neuen Mittelwert und Varianz erhält man?
| xi | xi² |
|---|---|
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 6 | 36 |
| 8 | 64 |
| 10 | 100 |
| 33 | 229 |
1 Mittelwert und Varianz:
Mittelwert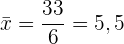
Varianz
2 Wenn alle Maße der Variablen mit 3 multipliziert werden, ist der Mittelwert 3mal so hoch und die Varianz wird mit 3 zum Quadrat multipliziert.
Mittelwert
Varianz
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
