Kapitel
Gegeben sind folgende Matrizen:
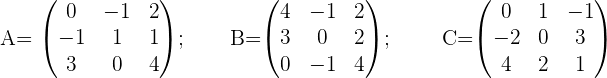
Berechne:
1 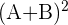
2 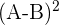
3 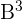
4 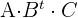
1 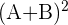
Wir berechnen 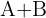 . Dazu addieren wir die Elemente, die in beiden Matrizen an der gleichen Stelle stehen
. Dazu addieren wir die Elemente, die in beiden Matrizen an der gleichen Stelle stehen
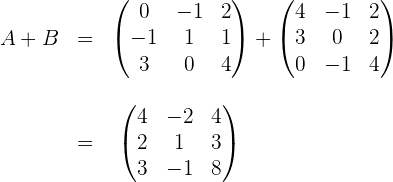
Wir quadrieren das vorhergehende Ergebnis
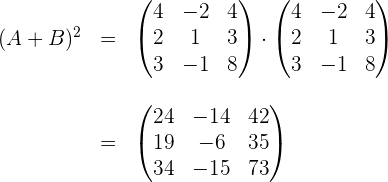
2 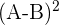
Wir berechnen 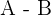
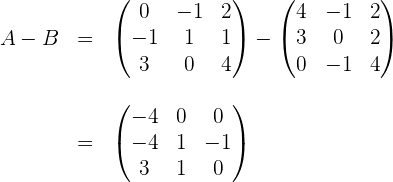
Wir quadrieren das vorhergehende Ergebnis

3 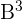
Zuerst berechnet man 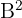 und dann multipliziert man mit
und dann multipliziert man mit 

4 
Wir berechnen 

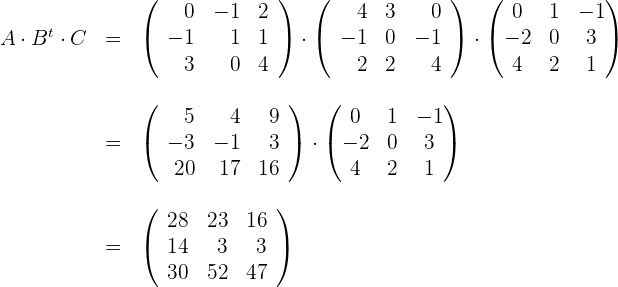

Produkt und Dimension von Matrizen
Gegeben sind die Matrizen:
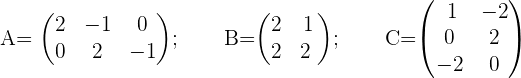
1 Beweise, ob die folgenden Produkte möglich sind:
a 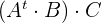
b 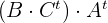
2 Die Dimension von  bestimmen, um die Multiplikation
bestimmen, um die Multiplikation 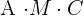 durchführen zu können
durchführen zu können
3 Die Dimension von  bestimmen, damit
bestimmen, damit  eine quadratische Matrix ist.
eine quadratische Matrix ist.
1
a Das Ergebnis der Multiplikation  ist eine Matrix der Form
ist eine Matrix der Form 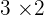 , da
, da  die Form
die Form 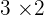 hat und
hat und  die Form
die Form  hat, während die Matrix
hat, während die Matrix  die Form
die Form 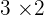 hat. Somit kann die Multiplikation nicht durchgeführt werden, weil die Anzahl der Spalten von
hat. Somit kann die Multiplikation nicht durchgeführt werden, weil die Anzahl der Spalten von  nicht mit der Anzahl der Zeilen von
nicht mit der Anzahl der Zeilen von  übereinstimmt.
übereinstimmt.
b Das Ergebnis der Multiplikation 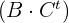 ist eine Matrix der Form
ist eine Matrix der Form  , da
, da  die Form
die Form  hat und
hat und 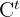 die Form
die Form  hat, während die Matrix
hat, während die Matrix  die Form
die Form 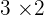 hat. Somit kann die Multiplikation durchgeführt werden, weil die Anzahl der Spalten von
hat. Somit kann die Multiplikation durchgeführt werden, weil die Anzahl der Spalten von 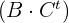 mit der Anzahl der Zeilen von
mit der Anzahl der Zeilen von  übereinstimmt und das Ergebnis ist eine Matrix der Form
übereinstimmt und das Ergebnis ist eine Matrix der Form 
2
Die Matrix  hat die Form
hat die Form  ;
;  hat die Form
hat die Form 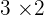 . Damit die Multiplikation durchgeführt werden kann, muss die Anzahl der Zeilen von
. Damit die Multiplikation durchgeführt werden kann, muss die Anzahl der Zeilen von  mit der Anzahl der Spalten von
mit der Anzahl der Spalten von  übereinstimmen und die Anzahl der Spalten von
übereinstimmen und die Anzahl der Spalten von  muss mit der Anzahl der Zeilen von
muss mit der Anzahl der Zeilen von  übereinstimmen. Somit hat
übereinstimmen. Somit hat  die Form
die Form 
3
Die Matrix  hat die Dimension
hat die Dimension 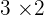 . Die transponierte Matrix hat deshalb die Form
. Die transponierte Matrix hat deshalb die Form  . Damit sie mit
. Damit sie mit  multipliziert werden kann, muss die Anzahl der Spalten von
multipliziert werden kann, muss die Anzahl der Spalten von 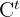 mit der Anzahl der Zeilen von
mit der Anzahl der Zeilen von  übereinstimmen und ihre Anzahl der Zeilen muss mit der Anzahl der Spalten von
übereinstimmen und ihre Anzahl der Zeilen muss mit der Anzahl der Spalten von  übereinstimmen. Somit hat
übereinstimmen. Somit hat  die Form
die Form 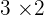
Matrizenmultiplikation
Mit welcher Zahl muss die Matrix
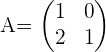
vorher multipliziert werden,
damit das Ergebnis die folgende Matrix ist
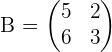
Wir stellen die gesuchte Matrix wie folgt dar
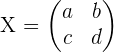
Wir lösen 
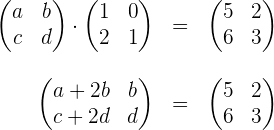
Wir erhalten folgendes Gleichungssystem
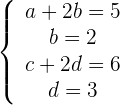
Wir lösen das System und erhalten
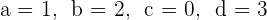
Somit ist die gesuchte Matrix

Kommutativität von Matrizen
Bestimme alle Matrizen, die mit der folgenden Matrix kommutieren:
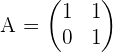
Wir stellen die gesuchte Matrix wie folgt dar
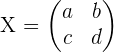 Wir lösen
Wir lösen 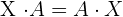
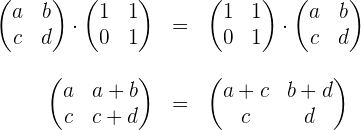
Wir erhalten das Gleichungssystem
Wir lösen das System und erhalten
Somit ist die gesuchte Matrix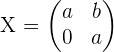 für irgendwelche reellen Werte von
für irgendwelche reellen Werte von 
Inverse Matrix
Berechne die inverse Matrix von:

1 Wir erstellen eine Matrix vom Typ 

2 Wir wenden die Gauß-Methode an und formen die linke Hälfte,  , zur Einheitsmatrix um. Die resultierende Matrix auf der rechten Seite ist unsere inverse Matrix
, zur Einheitsmatrix um. Die resultierende Matrix auf der rechten Seite ist unsere inverse Matrix  .
.
Wir rechnen 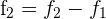
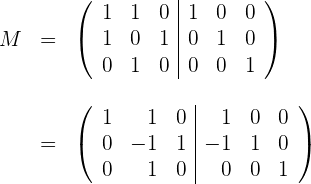
Wir rechnen 
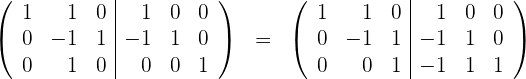
Wir rechnen 
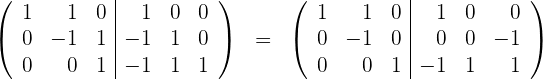
Wir rechnen  y
y 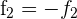
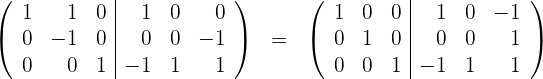
3 Die inverse Matrix ist
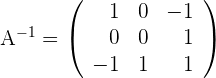
Rang einer Matrix
Berechne den Rang der folgenden Matrizen:


1 Matrix 
Wir führen die grundlegenden Rechenschritte bei den Zeilen durch:
1 Wir rechnen 

2 Wir berechnen die Determinante der Untermatrix
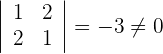
Daher gilt 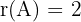 .
.
2 Matrix 
1 Wir stellen fest, dass 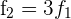 , weshalb gilt
, weshalb gilt 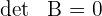
2 Wir berechnen die Determinante der Submatrix 
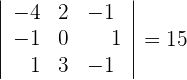
Deshalb gilt 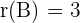 .
.
Matrizengleichungen
Gegeben sind:

Berechne den Wert von  in der Gleichung
in der Gleichung 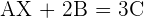
1 Wir bestimmen die Variable 
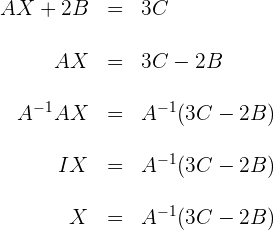
2 Wir berechnen 

3 Wir lösen auf und erhalten
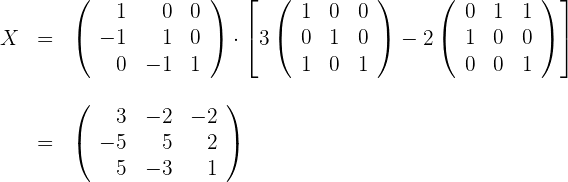
Anwendungsorientierte Aufgabe zu Matrizen
Ein Möbelhersteller produziert drei Modelle von Regalen:  und
und  . Jedes Regal ist in groß und in klein erhältlich. Jeden Tag werden
. Jedes Regal ist in groß und in klein erhältlich. Jeden Tag werden  große Regale und
große Regale und 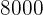 kleine Regale vom Modell
kleine Regale vom Modell  ,
, 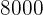 große und
große und 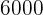 kleine Regale vom Modell
kleine Regale vom Modell  und
und 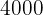 große und
große und 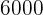 kleine Regale vom Modell
kleine Regale vom Modell  hergestellt. Jedes große Regal hat
hergestellt. Jedes große Regal hat  Schrauben und
Schrauben und  Halterungen. Jedes kleine Regal hat
Halterungen. Jedes kleine Regal hat  Schrauben und
Schrauben und  Halterungen. Dies gilt für alle drei Regaltypen.
Halterungen. Dies gilt für alle drei Regaltypen.
1 Stelle diese Information mit zwei Matrizen dar.
2 Erstelle eine Matrix, die die Menge der Schrauben und Halterungen, die bei der täglichen Produktion jedes einzelnen der sechs Modelle benötigt werden, beinhaltet.
1 Informationen in zwei Matrizen.
Zeilen: Modelle  , Spalten: Typen
, Spalten: Typen 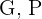
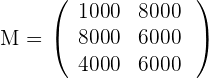
Matrix der Elemente der Regale:
Zeilen: Typen 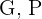 , Spalten:
, Spalten: 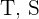
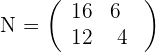
2 Erstelle eine Matrix, die die Menge der Schrauben und Halterungen, die bei der täglichen Produktion jedes einzelnen der sechs Modelle benötigt werden, beinhaltet.
Matrix, die die Anzahl der Schrauben und Halterungen für jedes Regalmodell ausdrückt:
Zeilen: Modelle  ; Spalten: Typen
; Spalten: Typen 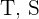

Mit KI zusammenfassen:













