Bestimme den Rang der Matrizen
Bestimme den Rang der folgenden Matrizen, indem du die linear unabhängigen Zeilen ermittelst:

Wir denken daran, dass wir die i-te Zeile als Fi notieren. Wir machen mit der Bestimmung der linear unabhängigen Zeilen (nicht null) weiter. Dazu analysieren wir sie der Reihe nach.

 . Es existiert keine reelle Zahl
. Es existiert keine reelle Zahl  , sodass
, sodass 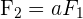 . Deshalb sind sie linear unabhängig.
. Deshalb sind sie linear unabhängig. . Wir stellen fest, dass
. Wir stellen fest, dass 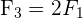 . Deshalb sind sie nicht linear unabhängig
. Deshalb sind sie nicht linear unabhängig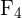 . Diese Zeile ist null (alle ihre Einträge sind
. Diese Zeile ist null (alle ihre Einträge sind  ).
). . Wir haben
. Wir haben  , weshalb sie auch nicht linear unabhängig sind mit
, weshalb sie auch nicht linear unabhängig sind mit  und
und  .
.
In Anbetracht dessen, was wir herausgefunden haben, wissen wir, dass wir nur  linear unabhängige Zeilen haben, nämlich
linear unabhängige Zeilen haben, nämlich  und
und  . Somit ist unser Rang
. Somit ist unser Rang 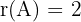 .
.
Berechne mit dem Gauß-Jordan-Algorithmus den Rang der Matrix (I)
Berechne mit dem Gauß-Jordan-Algorithmus den Rang der folgenden Matrix:
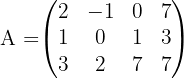
Wir denken daran, dass der Rang der Matrix der Anzahl der Nichtnullzeilen, die wir nach Abschluss des Gauß-Jordan-Algorithmus erhalten, entspricht. Somit können wir mit der Methode beginnen

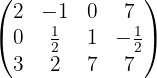
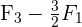
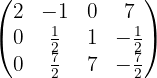
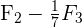
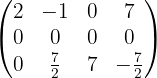

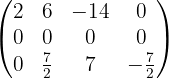
Somit ist unsere Matrix
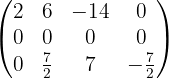
Sie hat zwei Nichtnullzeilen, weshalb gilt: 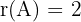
Berechne mit dem Gauß-Jordan-Algorithmus den Rang der Matrix (II)
Berechne mit dem Gauß-Jordan-Algorithmus den Rang der folgenden Matrix:
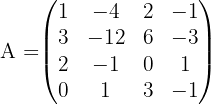
Wir denken daran, dass der Rang der Matrix der Anzahl der Nichtnullzeilen, die wir nach Abschluss des Gauß-Jordan-Algorithmus erhalten, entspricht. Somit können wir mit der Methode beginnen

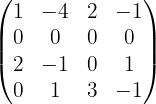

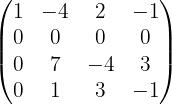

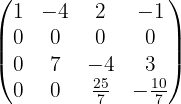
Wir könnten mit der Methode weitermachen, allerdings ist das nicht nötig, da wir für 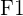 oder
oder  nicht null erhalten, indem wir von ihnen irgendein Vielfaches von
nicht null erhalten, indem wir von ihnen irgendein Vielfaches von 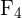 abziehen. Somit ist unsere Matrix
abziehen. Somit ist unsere Matrix
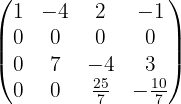
Die Matrix hat drei Nichtnullzeilen, weshalb gilt: 
Bestimme anhand der Determinanten den Rang der Matrix (I)
Bestimme anhand der Determinanten den Rang der Matrix:
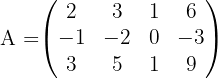
Wir denken daran, dass der Rang der Matrix der Ordnung der größten quadratischen Submatrix, die nicht null ist, entspricht. Bei der Berechnung der Ränge ergibt sich daher Folgendes:
Untermatrizen der Dimension 1. Da die Matrix nicht null ist, existiert daher irgendeine Untermatrix der Dimension eins mit einer Determinanten ungleich 0, zum Beispiel: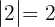
Untermatrizen der Dimension 2. Wenn wir eine Untermatrix der Dimension 2 mit einer Determinanten ungleich null haben, wissen wir, dass der Rang größer oder gleich 2 ist. Wir stellen also fest, dass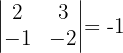
Deshalb ist die Dimension mindestens 2.
Untermatrizen der Dimension 3. Wenn wir eine Untermatrix der Dimension 3 mit einer Determinanten ungleich null haben, wissen wir, dass der Rang der Matrix größer oder gleich 3 ist. Wir stellen also fest, dass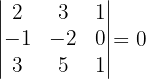
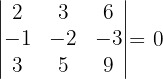


Da alle Untermatrizen der Dimension 3 die Determinanten null haben, ist der Rang der Matrix  .
.
Folglich ergibt sich 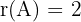 .
.
Bestimme anhand der Determinanten den Rang der Matrix (II)
Bestimme anhand der Determinanten den Rang der Matrix:
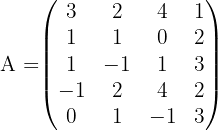
Wir denken daran, dass der Rang der Matrix der Ordnung der größten quadratischen Submatrix, die nicht null ist, entspricht. Wir stellen nun fest, dass die Dimension 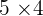 ist. Deshalb ist der Rang höchstens 4. Wenn wir jedoch eine Untermatrix der Dimension
ist. Deshalb ist der Rang höchstens 4. Wenn wir jedoch eine Untermatrix der Dimension  mit der Determinante ungleich null haben, ist der Rang der Matrix
mit der Determinante ungleich null haben, ist der Rang der Matrix  . Wir stellen also fest, dass:
. Wir stellen also fest, dass:
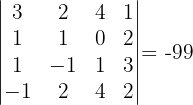
Folglich ergibt sich 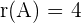 .
.
Bestimme anhand der Determinanten den Rang der Matrix (III)
Bestimme anhand der Determinanten den Rang der Matrix:

Wir denken daran, dass der Rang der Matrix der Ordnung der größten quadratischen Submatrix, die nicht null ist, entspricht. Außerdem können wir die Spalten oder Zeilen, die null oder linear abhängig zu anderen sind, streichen. Die dritte Spalte ist null, die vierte Spalte ist ein Vielfaches der ersten (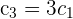 ). Die fünfte Spalte ist schließlich eine lineare Kombination aus der ersten und der zweiten (
). Die fünfte Spalte ist schließlich eine lineare Kombination aus der ersten und der zweiten ( ). Somit bleiben uns nur noch die ersten zwei Spalten:
). Somit bleiben uns nur noch die ersten zwei Spalten:
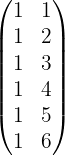
Wir stellen fest, dass wir für diese Matrix höchstens Untermatrizen der Dimension  erhalten können. Wir berechnen also die Determinante einer Submatrix der Dimension
erhalten können. Wir berechnen also die Determinante einer Submatrix der Dimension  wie folgt:
wie folgt:
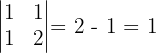
Somit ist der Rang 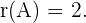
Bestimme anhand der Determinanten den Rang der Matrix (IV)
Bestimme anhand der Determinanten den Rang der Matrix:
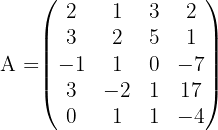
Wir denken daran, dass der Rang der Matrix der Ordnung der größten quadratischen Submatrix, die nicht null ist, entspricht. Außerdem können wir die Spalten oder Zeilen, die null oder linear abhängig zu anderen sind, streichen. Wir stellen fest, dass die dritte Spalte die Summe aus den ersten zwei Spalten ist (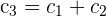 ). Somit bleibt uns noch die folgende Matrix, bei der wir unsere Methode anwenden.
). Somit bleibt uns noch die folgende Matrix, bei der wir unsere Methode anwenden.
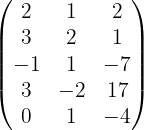
Untermatrizen der Dimension 1. Da die Matrix nicht null ist, existiert eine Untermatrix der Dimension eins mit der Determinante ungleich 0, zum Beispiel: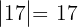
Untermatrizen der Dimension 2. Wenn wir eine Submatrix der Dimension 2 mit der Determinante ungleich null haben, wissen wir, dass der Rang größer oder gleich 2 ist. Wir stellen also fest, dass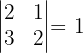
Somit ist die Dimension mindestens 2.
Untermatrizen der Dimension 3. Wenn wir eine Untermatrix der Dimension 2 mit der Determinante ungleich null haben, wissen wir, dass der Rang der Matrix größer oder gleich 3 ist. Wir stellen also fest, dass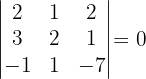
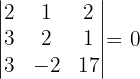
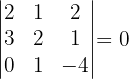
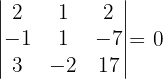
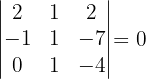
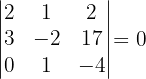
Da alle Untermatrizen der Dimension drei die Determinante null haben, ist der Rang der Matrix  .
.
Deshalb gilt 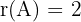 .
.
Mit KI zusammenfassen:



